Notes are incomplete, but include copies of what was presented in class. Notes will be completed as soon as feasible.
Section 9.6.
Let P_0 = (2, 4, 5), P_1 = (4, 7, -2) and P_2 = (8, 1, -1).
Corrections to figure below:
u = P_01 = 2 `i + 3 - 7 `k.
w = P_12 = 4 `i - 6 `j + `k
P_02 = 6 `i - 3 `j - 4 `k.
u X w = -4 `i - 7 `j - 30 `k
(corrected figure will be posted)
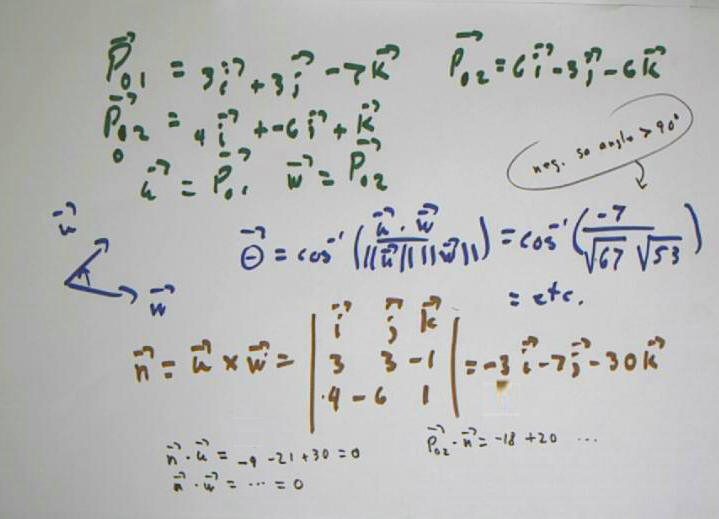
(still doesn't really work out because of error in n vector, but very nearly)
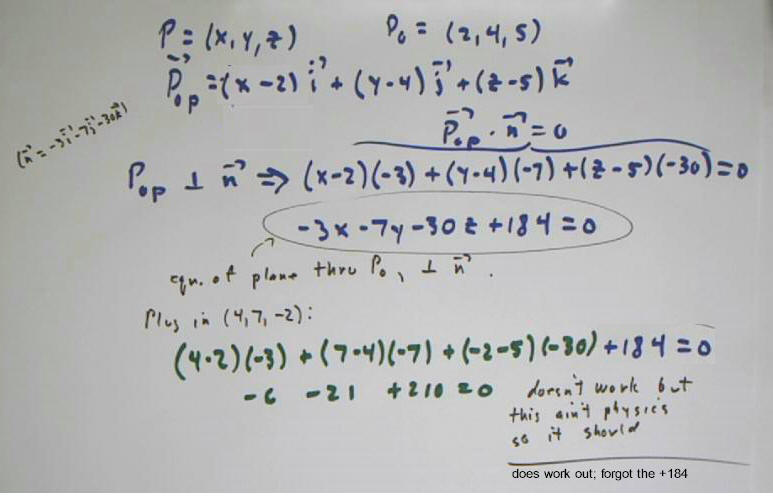
The vector from P0 to general point P = (x, y, z) is perpendicular to n provided a(x - x0) + b(y - y0) + c(z - z0) = 0.
So 2 x + 3 y - 5 z = 30 is the equation of a plane perpendicular to 2 `i + 3 `y - 5 `k.
- This plane contains a point corresponding to x = 2 and y = 4. The z coordinate must be -16/5. So (2, 4, -16/5) lies on the plane.
- The intersection of the plane with the x axis occurs when y = z = 0, at the point (0, 0, -6), easily found by substituting 0 for y and z in the equation 2 x + 3 y - 5 z = 30.
- Intersections with y and z axes are also easily found to be (15, 0, 0) and (0, 10, 0).
- The sketch indicates these three points with lines and shading representing the triangle with vertices at these points.
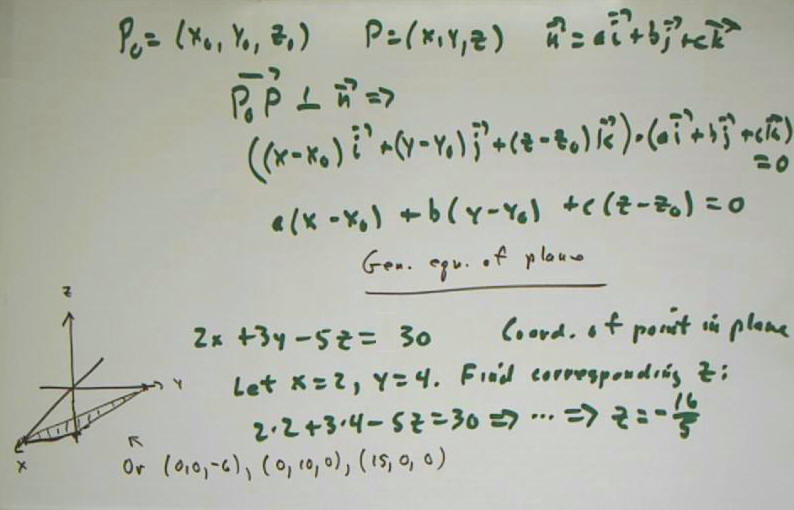
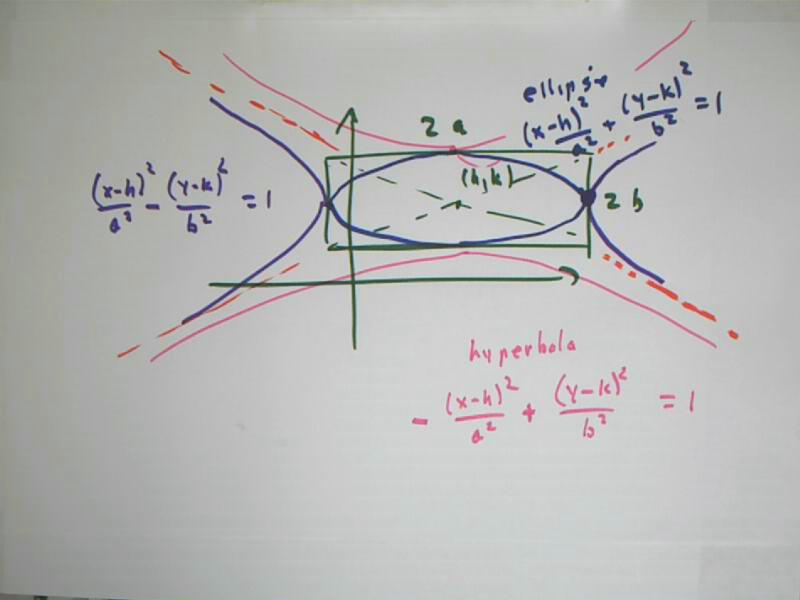
Notes corresponding to Section 9.7:
The ellipse (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1 is inscribed in the rectangle of dimensions 2 a by 2 b, centered at (h, k) (blue).
The hyperbola (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1 is asymptotic to the lines defined by the diagonals of the rectangle, with vertices on the rectangle. It is not possible for x to take value h on this hyperbola, since this would lead to - (y - k)^2 / b^2 = 1 and a negative quantity can't equal a positive quantity. So the 'pink' graph, which contains points corresponding to x = h, is not possible and the 'purple' graph corresponds to this form.
The hyperbola - (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1 is asymptotic to the lines defined by the diagonals of the rectangle, with vertices on the rectangle. It is not possible for x to take value k on this hyperbola, since this would lead to - (x - h)^2 / a^2 = 1 and a negative quantity can't equal a positive quantity. So the 'purple' graph, which contains points corresponding to y = k, is not possible and the 'pink' graph corresponds to this form.
For z = 1 the graph of x^2 / 25 + y^2 / 4 - z^2 = 0 corresponds to an ellipse centered at the origin of an x-y system, with semimajor axes 5 and 2. This ellipse is the intersection of the plane z = 1 (the plane 1 unit above the x-y plane in the xyz coordinate system), and the graph of the quadric surface defined by x^2 / 25 + y^2 / 4 - z^2 = 0.
For z = 2 we get a similar ellipse, but with twice the dimensions of the first.
For z = 4 we get a similar ellipse, but with four times the dimensions of the first.
If we visualize these ellipses in xyz space we can see that they indicate a shape with the following characteristics:
- The intersections with planes parallel to the x-y plane are ellipses centered on the z axis, whose dimensions increase linearly with | z |.
- The resulting surface is therefore much like a cone parallel to the z axis, with apex at the origin (0, 0, 0). However the cone is 'squashed' in the y direction, so that rather than being circles, the cross-sections are ellipses.
- The dimensions being proportional to | z | the intersections of this figure with the xz and yz planes are straight lines through the origin, with respective slopes 5 and 2.
- The intersection of any vertical plane with this surface forms a hyperbola, in the same way the intersection of a cone with a plane parallel to its axis forms a hyperbola.
- This particular surface is therefore called an 'elliptic hyperboloid'.
