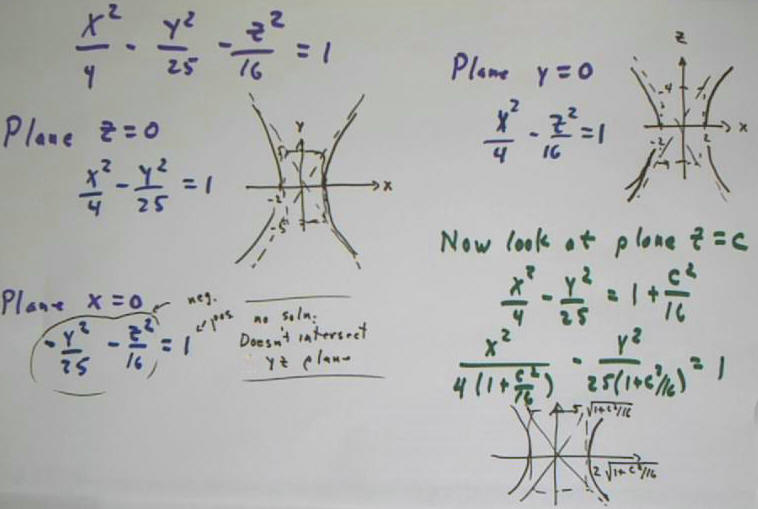
We consider the graph of the equation x^2 / 4 - y^2 / 25 - z^2 / 16 = 1. The set of points that satisfy this equation form a surface in 3-dimensional space. We wish to explore the shape of that surface.
- In the plane z = 0, i.e., the xy plane, the equation becomes x^2 / 4 - y^2 / 25 = 1. This is the equation of a hyperbola, constructed using the rectangle shown in the corresponding figure. The intersection of the surface with the x-y plane is this hyperbola.
- In the plane x = 0, the y z plane, we get the equation -y^2 / 25 - z^2 / 16 = 1. The left-hand side is negative, the right-hand side positive, so there is no solution to this equation. The surface therefore does not intersect the y z plane.
- In the plane y = 0, the x z plane, we get another hyperbola.
- The plane z = c is a horizontal plane, parallel to the xy plane but lying at vertical displacement c from this plane. Substituting z = c into our original equation we get x^2 / 4 - y^2 / 25 - c^2 / 16 = 1, so that x^2 / 4 - y^2 / 25 = 1 + c^2 / 16. Putting this into standard form we find that the graph is a hyperbola, geometrically similar to the one obtained for z = 0 but scaled up by a factor of sqrt(1 + c^2 / 16). So as c increases, i.e., as our z = c plane gets higher and higher above the xy plane, its intersection with the surface remains a hyperbola, but the hyperbola 'expands'.
The figure below shows how the hyperbolas expand as c increases from 0 to 4 to 8.
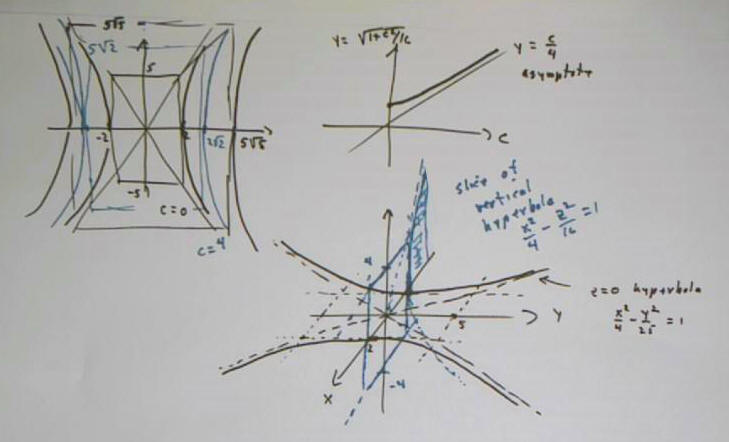
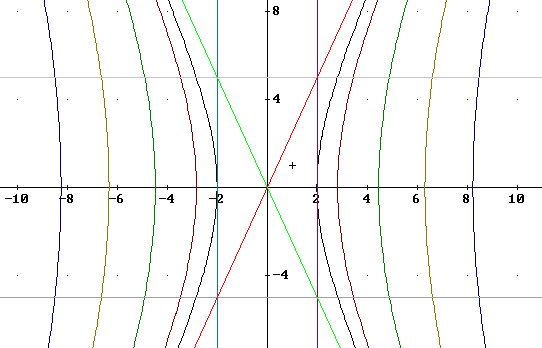
The hyperbolas x^2/4 - y^2/25 = 1 + c^2 / 16, for c = 0, 4, 8, 12, 16. The lines x = +-2, y = +-5, y=+-5/2 x are also plotted and form the 'box' and diagonals for the c = 0 graph.
Visualize these hyperbolas as contour lines of the surface, from lowest to highest. These contour lines are the intersections of the quadric surface x^2 / 4 - y^2 / 25 - z^2 / 4 = 1 with the planes z = 0, z = 4, z = 8, z = 12, z = 16.
- Note that the vertices of the hyperbolas are unequally spaced, indicating that if you were to 'climb' the surface by proceeding from the origin in the x direction, starting at x = 2, you would start out climbing a very steep surface, but the slope would quickly begin to level out.
The equations of the above surfaces are
- x^2/4 - y^2/25 = 1,
- x^2/4 - y^2/25 = 2,
- x^2/4 - y^2/25 = 5,
- x^2/4 - y^2/25 = 10,
- x^2/4 - y^2/25 = 17.
If each equation is put into its standard form you will easily get the dimensions of the 'box' and resulting asymptotes required to graph each of the hyperbolas.
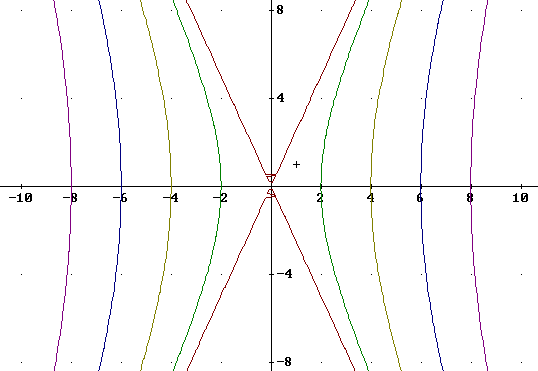
By contrast we see the hyperbolas x^2/4 - y^2/25 = c^2 / 16 (rather than 1 + c^2 / 16), again for c = 0, 4, 8, 12, 16.
Note four things:
- The first 'hyperbola' (not really a hyperbola), for c = 0, just consists of the two straight lines y = +- 5/2 x.
- The vertices of the remaining hyperbolas are spaced equally, unlike before.
- If you were to 'climb' this surface in the direction of the x axis, you could start climbing at x = 0, and your climb would be characterized by constant steepness. You would in fact be climbing the side of a cone.
- As you go from one hyperbola to the next, you can compare where you are with where you would be on the previous figure. You will see that the hypberolas get closer and closer to those shown there.
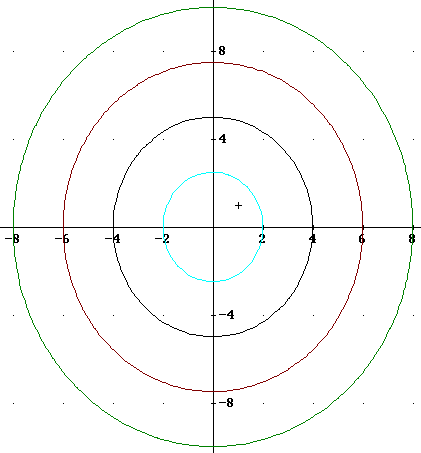
Intersections with planes x = c for c = 1, 2, 3, 4 are the ellipses y^2/25 + z^2 / 16 = c^2 / 4.