Position vector `r(t) = (x(t), y(t) ), for some t interval a < t < b, traces out a curve in the plane. We will understand the parameter t in this example to stand for clock time.
At t = t0, the position on the curve is `r(t0) = (x(t0), y(t0) ).
After a short interval `dt the parameter is t = t0 + `dt and the position on the curve is (x(t0 + `dt), y(t0 + `dt) ).
The average velocity of the point during the interval from t0 to t0 + `dt is the average rate of change of its position with respect to clock time, which is (change in position) / (change in clock time) = (final position - initial position) / `dt. We get
v_Ave = ( (x(t0 + `dt), y(t0 + `dt) ) - (x(t0), y(t0) ) ) / `dt, which simplifies to
v_Ave = ( (x(t0 + `dt) - x(t0)), (y(t0 + `dt) - y(t0) ) / `dt
= ( (x(t0 + `dt) - x(t0) / `dt,(y(t0 + `dt) - y(t0) ) / `dt)
= ( vx_ave, vy_ave)
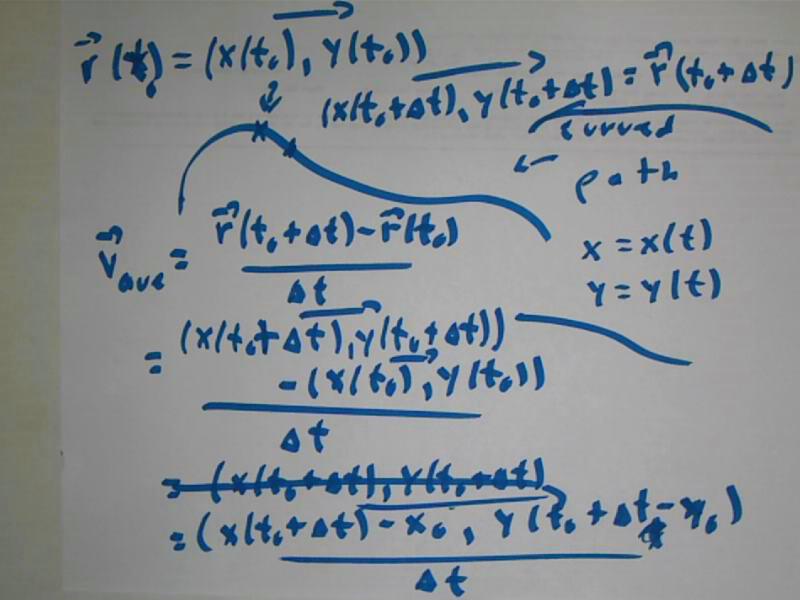
v_Ave = ( vx_ave, vy_ave) is the average velocity on the interval. If we let `dt approach zero, then in the limit we get
v(t0) = (vx(t0), vy(t0)), where vx and vy are the instantaneous velocities in the x and y directions, at clock time t0.
We sketch the `r(t0) and `v(t0) vectors.
The `v(t0) vector has
a magnitude, which is the speed of the point, and a direction, which is
the direction in which the point is moving at the t = t0 instant.

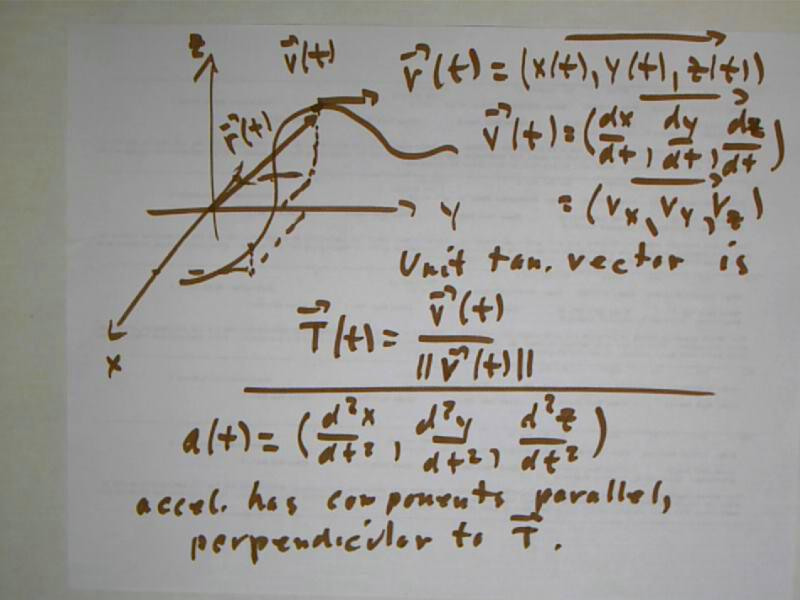
Similarly `r(t) = (x(t), y(t), z(t)) can represent an object moving in 3-dimensional space.
We can take the derivatives of the three functions and get the velocity vector `v(t).
If we divide `v(t) by its magnitude we get a unit vector `T(t) = `v(t) / || `v(t) || , the direction of which is tangent to the curve.
If we take another derivative we get the
acceleration vector `a(t). In general the vector `a(t) is expected
to have components in the direction of the unit tangent vector `T(t),
called the parallel component, and perpendicular to the unit tangent
vector, called the perpendicular component.
The component of the vector `a(t) in the direction of `T(t) is seen to be just the projection `a_T (t) = `a(t) dot `T(t) * `T(t), since || `T(t) || = 1. This component indicates the rate of change of the speed of motion in the direction of motion, and the direction of that rate.
The vectors `T(t) and `a_T(t) form two sides of a right triangle. The third side, running from the terminal point of `a_T(t) to the terminal point of `a, is the vector `a(t) - `a_T (t). This vector is perpendicular to `T(t).
The vector `N(t) = ( `a(t) - `a_T (t) ) / || `a(t) - `a_T (t) || is therefore a unit vector perpendicular to `T(t).
The vectors `T(t) and `N(t) therefore constitute a set of coordinate axes in the plane of the velocity and acceleration vectors.
The cross product of these vectors, being the cross product of perpendicular unit vectors, is also a unit vector. We call it the binormal vector `B(t). The binormal vectors is perpendicular to the plane of `T(t) and `N(t), and with these two vectors provides us with a moving three-dimensional coordinate system. As the point moves, the plane of the acceleration and velocity vectors changes, and the direction of the binormal vector changes with them.

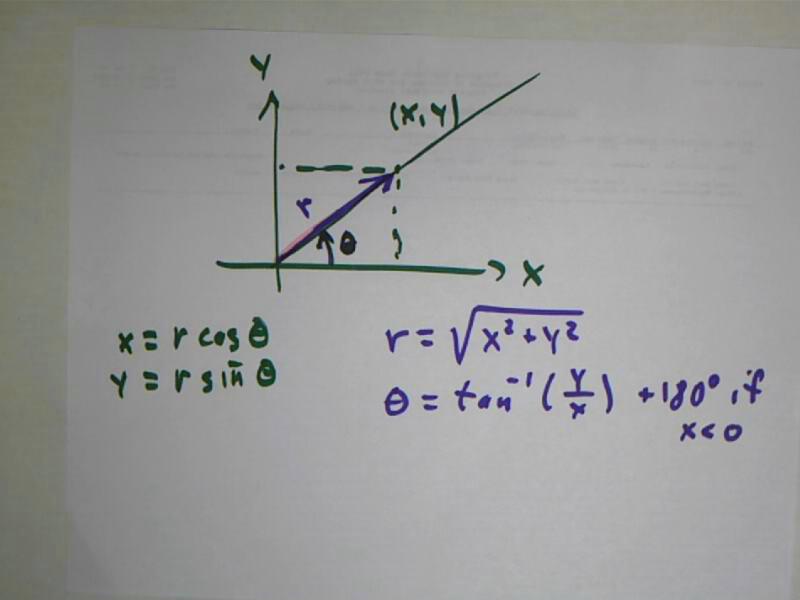
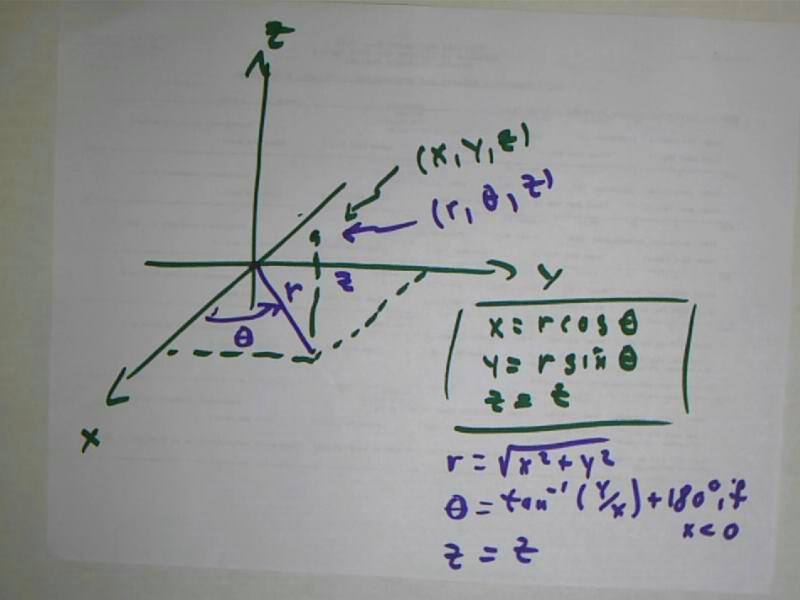
A point in the plane can be specified by its x and y coordinates, in the familiar fashion.
Alternatively it can be specified by its distance r from the origin, and by the angle of the ray originating at the origin and extending through the point with the polar axis. (The polar axis is a ray originating at the origin).
If the polar axis coincides with the positive x axis, then if the x and y coordinates of the points are x and y, the r and theta coordinates are r = sqrt(x^2 + y^2) and theta = arcTan(y / x), plus 180 deg or pi radians if x < 0. If the polar coordinates are r and theta, then the x coordinate is x = r cos(theta) and the y coordinate is y = r sin(theta).
This topic should be familiar from precalculus. You can see more about polar coordinates at
http://vhcc2.vhcc.edu/pc2fall9/lectures/990311/class_notes.htm
This document also appears on your DVD, and the video links work on the disk. If you search for the 990311 subfolder you can easily find the file.
Cylindrical coordinates are closely related to polar coordinates. Any point in x-y-z space can be defined by the point in the x-y plane directly below the point (i.e., the projection point when the point is projected onto the x-y plane) and the polar coordinates of that point. The z coordinate is the displacement of the point above the xy plane (negative if the point is below the plane).
The relationship between x and y coordinate, and r
and theta coordinates, is identical to that for polar coordinates.
The z coordinates are the same in both systems.
One example of the use of polar coordinates:
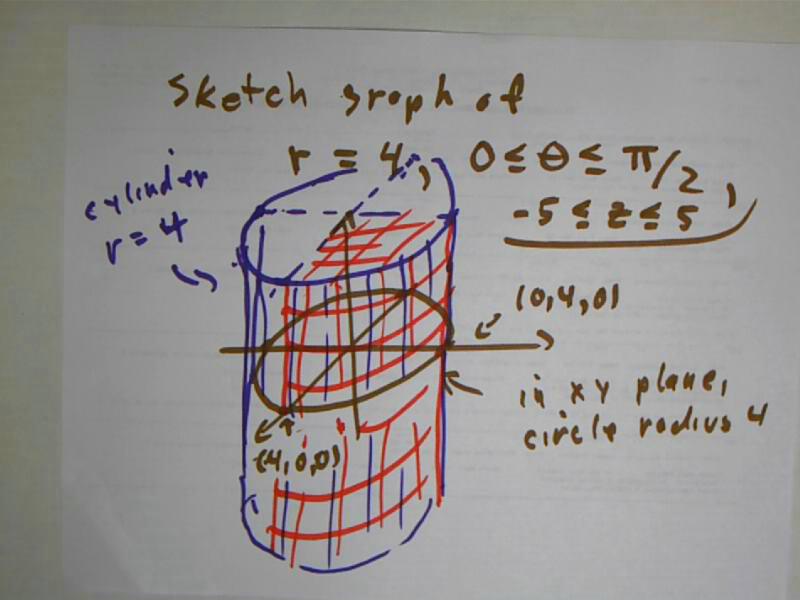
We sketch the graph of r = 4, 0 <= theta <= pi/2, -5 <= z <= 5.
In the x-y plane, r = 4 describes a circle of radius 4 centered at the origin. z can take any value between -5 and 5, so we extend each point of the circle 5 units above and 5 units below the axis, forming a cylinder of radius 4 and altitude 10.
The restriction 0 <= theta <= pi/2 restricts our points in the x-y plane to the first quadrant. This restricts our graph to points above and below the first quadrant. The surface is indicated in red in the figure below. The top has been shaded, which is incorrect. r = 4 at all points on the surface of the cylinder, and does not include points for which r < 4.
Had the description been r <= 4, 0 <= theta <= pi/2, -5 <= z <= 5, then the object would have been a solid it would have been appropriate to shade the top.
You might think about, and try to sketch, the following related surfaces:
- 2 <= r <= 4, 0 <= theta <= 2 pi, -r <= z <= r
- r = 8 / pi * theta, 0 <= theta <= pi / 2, || z || <= r.
.
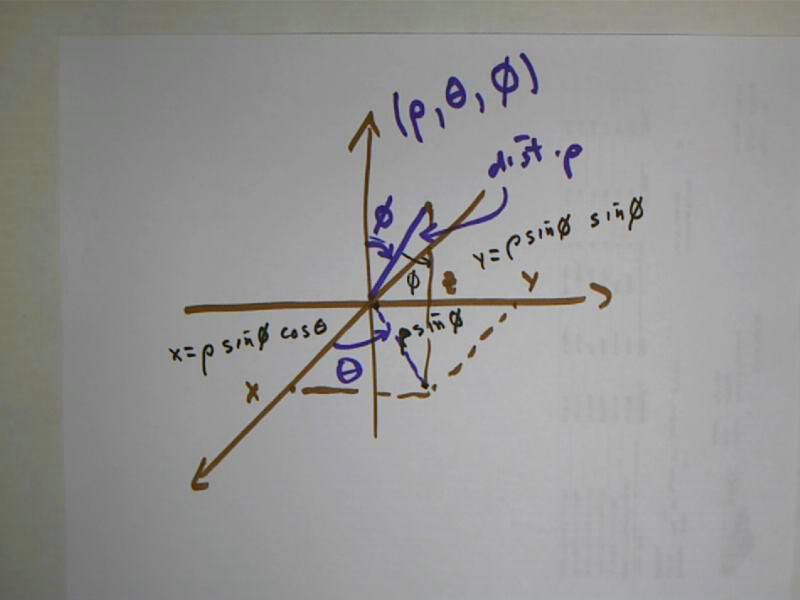
Spherical coordinates describe a point in terms of one distance and two angles.
We start with a point, and a ray starting at the origin and passing through the point. The angle phi is the angle of that ray with the z axis. rho is the distance of the point from the origin. The angle theta is found by first projecting the point into the xy plane, as we did with cylindrical coordinates; theta is the same as the angle theta for cylindrical coordinates.
The triangle with vertices at the point, the origin and the projection point (for the projection into the xy plane) has one side parallel to the z axis. The ray line from the origin to our point is a traversal of the two parallel lines, so the angle phi is at the 'top' of the triangle. The triangle is a right triangle with hypotenuse rho, so the side opposite the angle phi is rho sin(phi). This side would correspond to r in cylindrical coordinates.
The side of the triangle parallel to the z axis would be the z coordinate in polar coordinates. This side is rho cos(phi).
Thus the cylindrical coordinates of the point are r = rho sin(phi), z = rho cos(phi), and theta, which is the same in both systems.
The x coordinate of our point is x = r cos(theta) = rho sin(phi) cos(theta), and the y coordinate is y = r sin(theta) = r sin(phi) sin(theta).