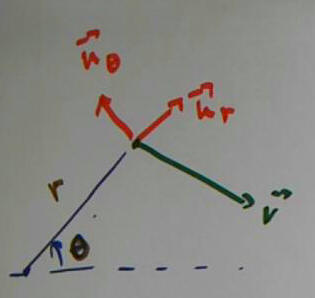
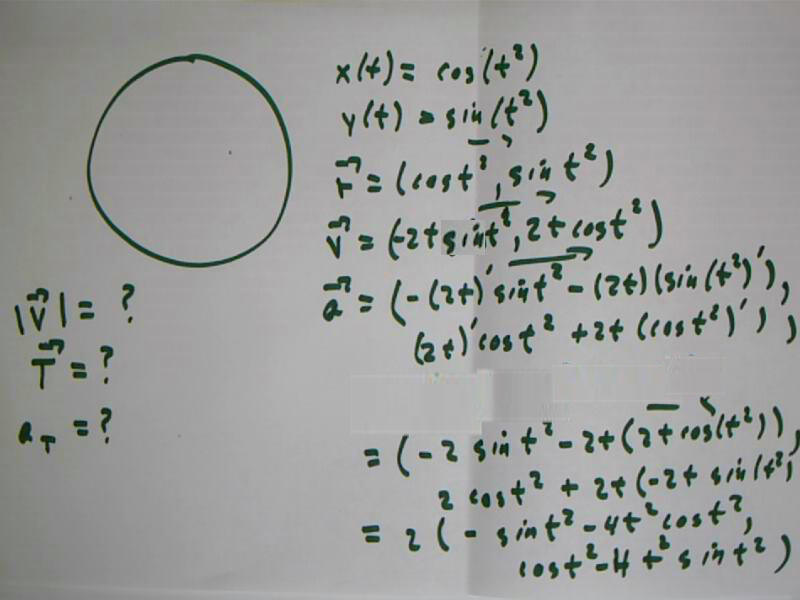The figure below shows the vectors u_r and u_theta for a point on a path in 2-dimensional space. The direection of u_r is always straight away from the pole or origin; the direction of u_theta is perpendicular to that of u_r , in the direction of increasing theta.
The velocity v has components in the directions of both vectors, with the greater component in the direction of u_theta.
The parametric equations x(t) = cos(t), y(t) = sin(t), 0 <= theta <= 2 pi correspond to a point moving around the unit circle at a constant speed.
The `r, `v and `a vectors are easily calculated. Each is a unit vector, so in this case the `v and `a vectors are the unit tangent and unit normal vectors.
It is easy to see that `v dot `r and `a dot `v are zero, proving that `v is perpendicular to `r and `a is perpendicular to `v.
It is intuitively obvious that anything we would call 'the curvature of a circle' is constant on a given circle, which is exactly as curvy at one point as at another.
So the curvature of this circle, which we have yet to define, is the same no matter how we parameterize it.

Now if x(t) = cos(omega * t) and y(t) = sin(omega * t), we obtain the results shown below for the `v and `a vectors.
The `v vector has constant magnitude omega, and the `a vector has constant magnitude omega^2.
If x(t) = A cos(omega * t) and y(t) = A sin(omega * t), we obtain for the `v and `a vectors the results shown below in red.
These results lead us to the conclusion that for this parameterization, || `a || = | `v | ^ 2 / A.
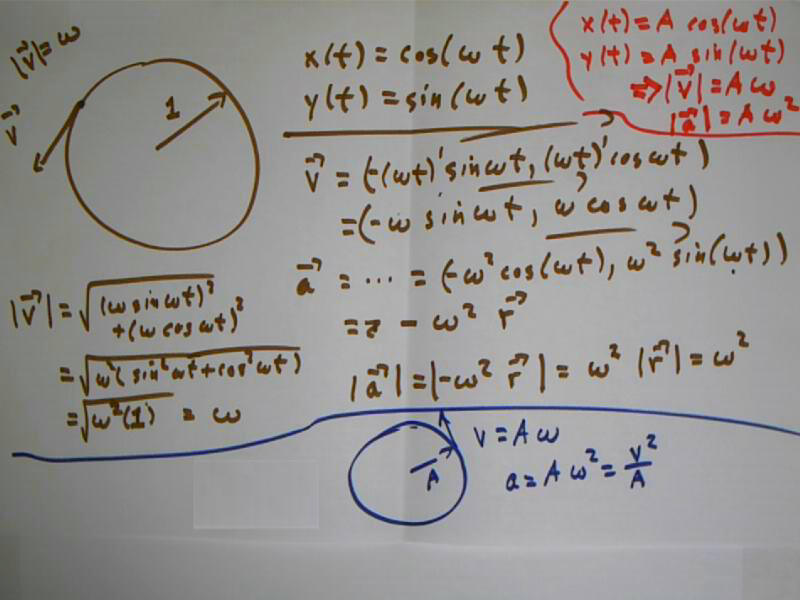

100915 notes
These notes follow the q_a_ questions for Section 10.2 and early Section 10.3. You should match them with your attempts at solutions.