We expand on the solution for the problem series beginning with `q001 on Section 10.3. We have already found the `R(t) vector, as repeated below.
- We find where the `j component is 20. The `j component at t is 10 + 20 t - 4.9 t^2. We set this equal to 20 and obtain solutions t = 3.5 and t = 0.5.
- Plugging t = 3.5 into the expression for `R(t) we obtain `R(3.5) = 35 `i + 20 `j, confirming that the `j component is 20 and revealing that the `i component at this instant is 35.
- Plugging t = 0.5 into the expression for `R(t) we obtain `R(0.5) = 5 `i + 20 `j, confirming that the `j component is 20 and revealing that the `i component at this instant is 5.
- The figure at lower left shows the path described by the `R(t) vector, the horizontal line defined by the condition that the `j component equal 20, and the two vectors `R(0.5) and `R(3.5). The vector `R(0) = 10 `j, which agrees with the given initial condition on `R(t), is also labeled.
This figure includes solutions to questions `q001 - `q004.
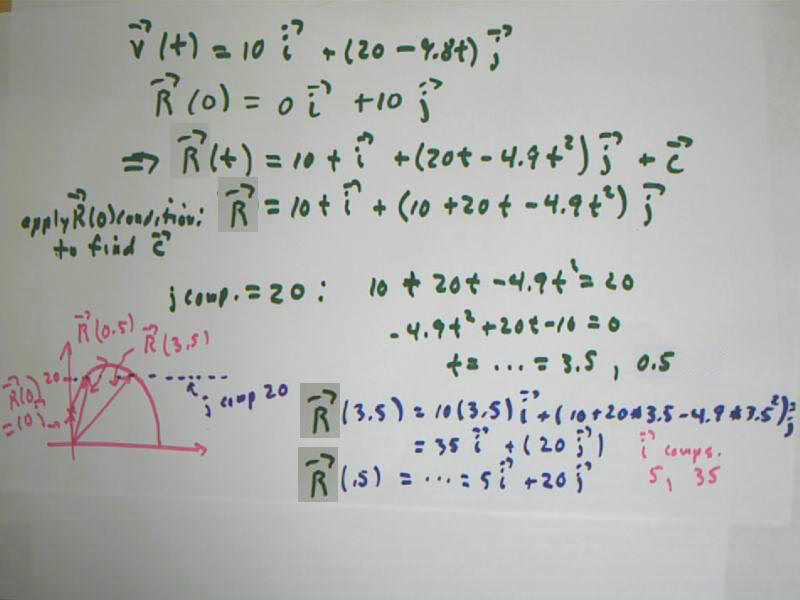
The `j component of the position is y(t). This component is maximized when the y(t) function is maximized. Setting y ' = 0 to obtain a critical point at t = 2.0 (approximated to 2 significant figures), then applying a second-derivative test, we conclude that this critical point yields a maximum.
Evaluating the y(t) function at t = 2.0 we obtain the maximum value of y, which is 30 (again approximating to 2 significant figures).
It isn't shown below but we easily evaluate that `i component of the position, which we find to be x(2) = 10 * 2 = 20.
- The projectile reaches its maximum height at t = 2, at which instant height is 30 and the x component of position is 20.
Using the dot product we find that the angle between the `R and `i vectors is 70 degrees when
cos(70 deg) = `R dot `i / ( || `R || || `i || ).
The dot product is just 10 t, and the magnitude of `i is 1, so we obtain cos(70 deg) = 10 t / ( || R || * 1). Evaluating cos(70 deg) we get .34, to two significant figures (note that the mental approximation .32 was used in the figure below). This yields the equation
.32 = 10 t / || R || = 10 t / (x(t)^2 + y(t)^2).
As noted in the figure below the resulting expression is easily found, but messy. Here are the remaining details:
Using the expressions for x(t) and y(t), and using .34 instead of .32, we obtain
.34 = 10 t / sqrt( (10 t)^2 + (10 + 20 t - 4.9 t^2) ), which with simplified denominator becomes
.34 = 10 t / sqrt( 24.01 t^4 - 196 t^3 + 402 t^2 + 400 t + 100). Squaring both sides we get
.34^2 = 100 t^2 / (24.01 t^4 - 196 t^3 + 402 t^2 + 400 t + 100). Multiplying both sides by the denominator and collecting terms on the left we obtain the equation
2.78 t^4 - 22.7 t^3 - 53.5 t^2 + 46.2 t + 11.56 = 0.
This equation could be solved analytically by factoring (very unlikely to factor over rational numbers), or by following the procedure for solving the quartic equation (impractical, even if you know the procedure). So it's fine to resort to technology. We obtain solutions
- t = 0.87, t = -0.21, t = -2.41 and t = 9.9,
all approximate. (Note that some liberties have been taken with significant figures).
At these clock times the cosine of the angle between the `R(t) vector and the `i vector may be about .34. All values of t at which this is so are included among these four values. However extraneous solutions can occur as a result of squaring both sides of the equation, so to be sure you would need to evaluate the `R(t) vector at each value of t, and check. In terms of what we currently know about the path of this projectile, only the solution t = -.21 appears to be viable.
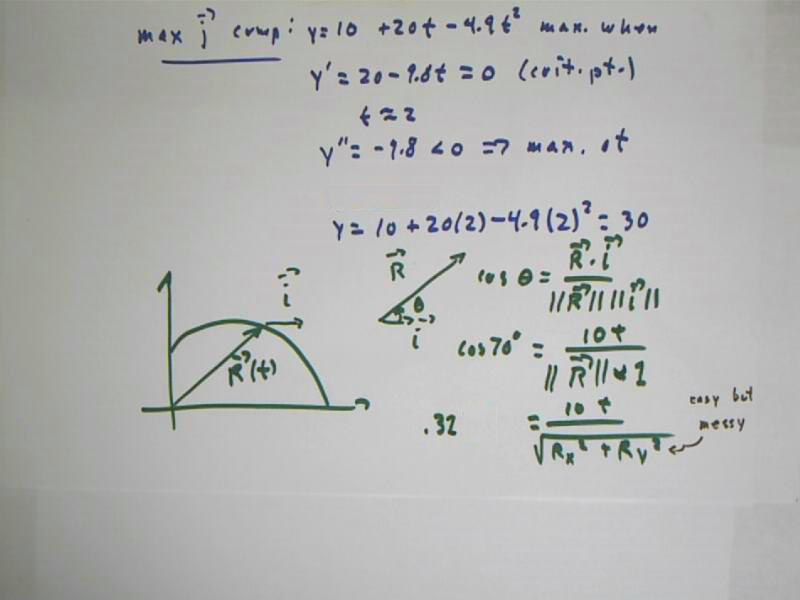
We easily eliminate t between the equations for x and y, solving the first to obtain t = x / 10 and substituting into the second to obtain y = -.049 x^2 + 2 x + 10.
Thus y is quadratic in t, resulting in a parabolic graph with vertex at x = 20. We could substitute x = 20 into the equation to get y = 30, giving us a parabola consistent with our previous solution for the maximum height, and the corresponding x coordinate.
This remainder of this document addresses the sequence of problems preceding the problem set for Section 10.4.
As we have seen in previous notes, the function `R(t) = A cos(omega t) `i + A sin(omega t) `j has the derivatives `v(t) and `a(t) as indicated below. We note the following properties of this function:
- The magnitude of `R(t) is identically equal to A (i.e., for any value of t we have || R(t) || = A).
- The magnitude of `v(t) is identically equal to omega * A.
- The magnitude of `a(t) is identically equal to omega^2 * `A.
- `v(t) is at every value of t perpendicular to `R(t), easily verified by taking the dot procut of `v and `R.
- `a(t) is at every value of t perpendicular to `v(t), easily verified by the dot product.
If R, v and a are the magnitudes of our three vectors for any value of t, it is easily verified that R = v^2 / a.
Now, greater values of omega imply a point moving around our circle with greater speed v and greater acceleration a. However, while speed and acceleration change when omega changes, the radius of the circle doesn't change as a result. Our expression v^2 / a, where v is the speed and a the acceleration perpendicular to the velocity, will always be the same, always equal to the radius of our circle.
The smaller the radius the more the circle is perceived to curve. So we define the curvature of circle to be
curvature = 1 / radius.
Using the lowercase Greek letter kappa for the curvature, we have
kappa = 1 / R = a / v^2.
Note that for the given circle R is equal to A.
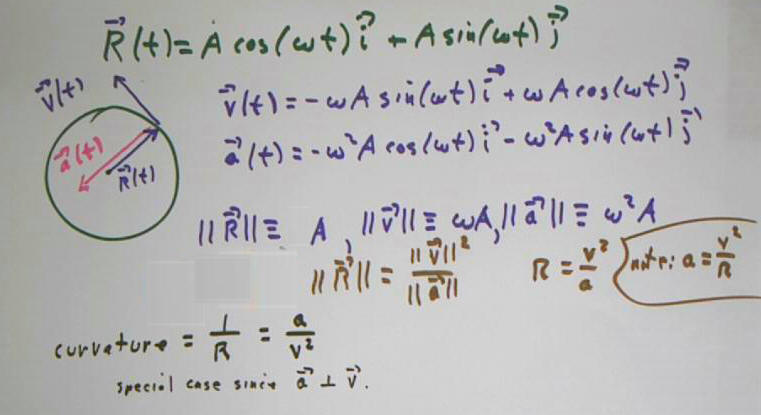
Now if we let `R(t) = a cos(omega * t^2) `i + `A sin(omega t^2) `j, we can easily calculate the `v(t) and `a(t) functions. This has been done in previous notes.
You should verify that || `v(t) || = 2 omega * t, indicating that the speed of the point is increasing.
You should also calculate the normal and tangential components of `a(t) (recall that you find the unit tangent vector, dot it with `a(t) to get the tangential component `a_T(t), then subtract the tangential component from `a(t) to get the normal component `a_N(t)).
You should then verify that || `a_N(t) || / || `v(t) || ^ 2 is equal to the curvature 1 / R = 1 / A for any value of t.
This example shows that despite the changing velocity and very different acceleration function, we obtain the same result as before for the curvature of the circle, provided only that we use the normal component `a_N of `a.
