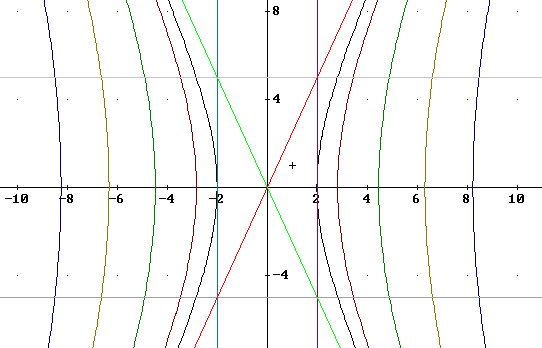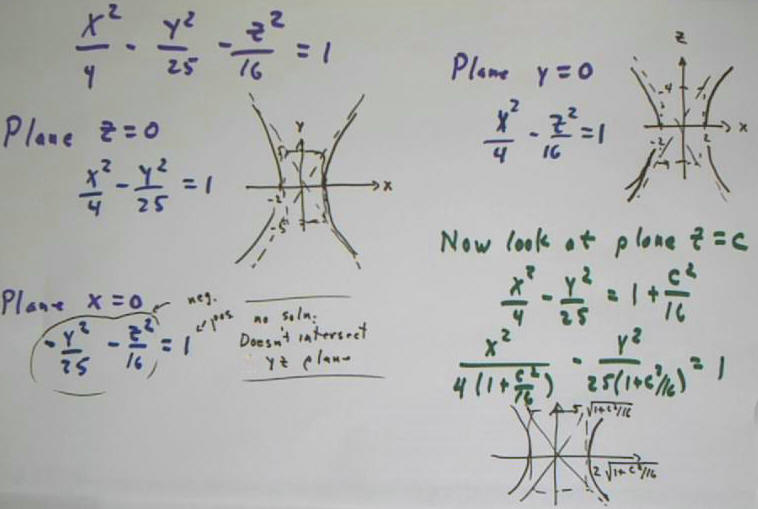
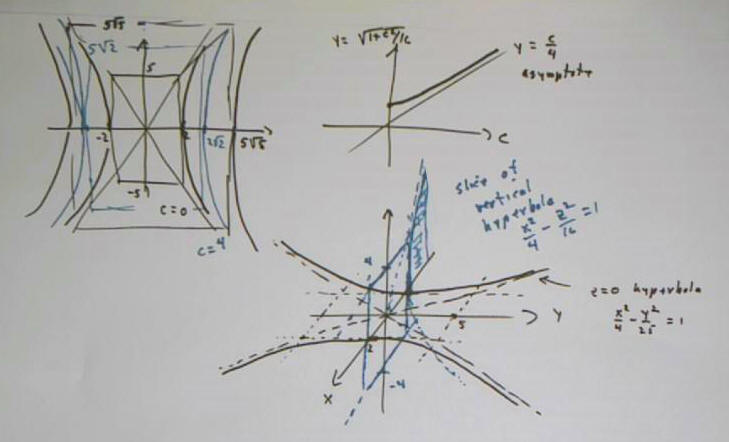
The hyperbolas x^2/4 - y^2/25 = 1 + c^2 / 16, for c = 0, 4, 8, 12, 16. The lines x = +-2, y = +-5, y=+-5/2 x are also plotted and form the 'box' and diagonals for the c = 0 graph.
Visualize these hyperbolas as contour lines of the surface, from lowest to highest. These contour lines are the intersections of the quadric surface x^2 / 4 - y^2 / 25 - z^2 / 4 = 1 with the planes z = 0, z = 4, z = 8, z = 12, z = 16.
- Note that the vertices of the hyperbolas are unequally spaced, indicating that if you were to 'climb' the surface by proceeding from the origin in the x direction, starting at x = 2, you would start out climbing a very steep surface, but the slope would quickly begin to level out.
The equations of the above surfaces are
- x^2/4 - y^2/25 = 1,
- x^2/4 - y^2/25 = 2,
- x^2/4 - y^2/25 = 5,
- x^2/4 - y^2/25 = 10,
- x^2/4 - y^2/25 = 17.
If each equation is put into its standard form you will easily get the dimensions of the 'box' and resulting asymptotes required to graph each of the hyperbolas.
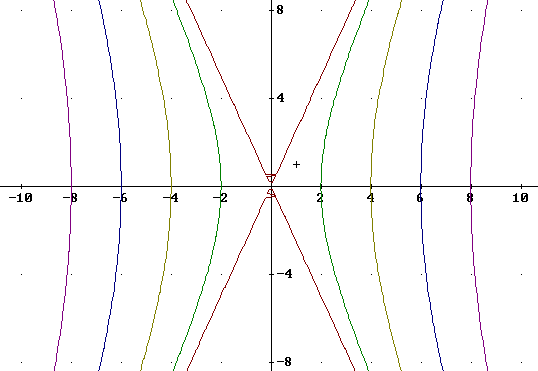
By contrast we see the hyperbolas x^2/4 - y^2/25 = c^2 / 16 (rather than 1 + c^2 / 16), again for c = 0, 4, 8, 12, 16.
Note four things:
- The first 'hyperbola' (not really a hyperbola), for c = 0, just consists of the two straight lines y = +- 5/2 x.
- The vertices of the remaining hyperbolas are spaced equally, unlike before.
- If you were to 'climb' this surface in the direction of the x axis, you could start climbing at x = 0, and your climb would be characterized by constant steepness. You would in fact be climbing the side of a cone.
- As you go from one hyperbola to the next, you can compare where you are with where you would be on the previous figure. You will see that the hypberolas get closer and closer to those shown there.
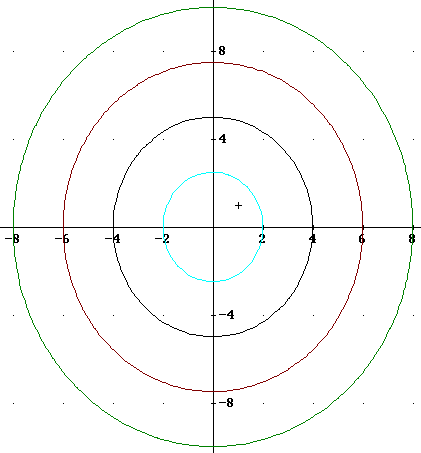
Intersections with planes x = c for c = 1, 2, 3, 4 are the ellipses y^2/25 + z^2 / 16 = c^2 / 4.