Notes from Class 101013

We're going to construct a rough picture of the ellipsoid

x^2 / 9 + y^2 / 25 + z^2 / 16 = 1.

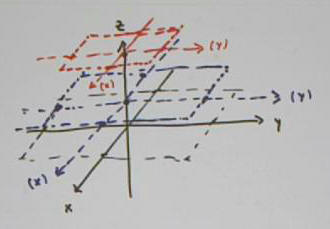
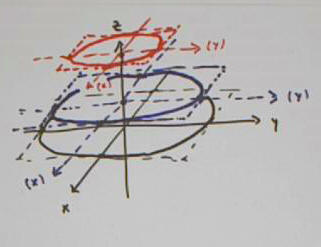
We begin by constructing the intersection of the ellipsoid with the planes z = 0, z = 1 and z = 3.

• In the plane z = c the graph is a function of x and y, with x^2 / 9 + y^2 / 25 = 1 - c^2 / 16.
• This can be rearraged to get x^2 / (9 * (1 - c^2/16) ) + y^2 / (25 * (1 - c^2/16) ) = 1.
• From this we see that the semimajor and semiminor axes are 5 sqrt( 1 - c^2 / 16) (in the y direction) and  3 sqrt( 1 - c^2 / 16) (in the x direction).

We plot the corresponding rectangles in below. 

For example to plot the c = 3 rectangle, indicated in red in the figure below:

We start by sketching auxiliary x and y axes centered at the z = 3 point of the z axis.  The auxiliary x axis is parallel to the x axis of the 3-dimensional coordinate system, and the auxiliary y axis parallel to the y axis of our 3-d coordinate system.

We mark points on these auxiliary axes, at x = +- 3 sqrt( 1 - 3^2 / 16) and y =  +-5 sqrt( 1 - 3^2 / 16).

We then sketch the rectangle passing through these points, with sides are parallel to the auxiliary axes.

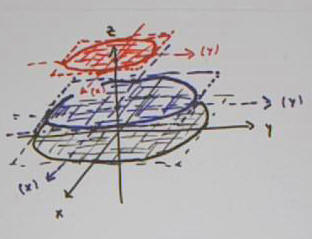
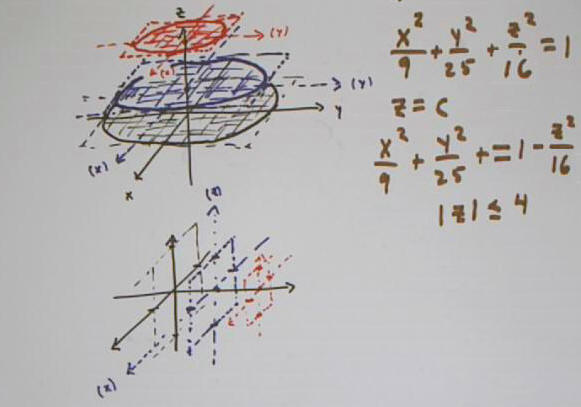
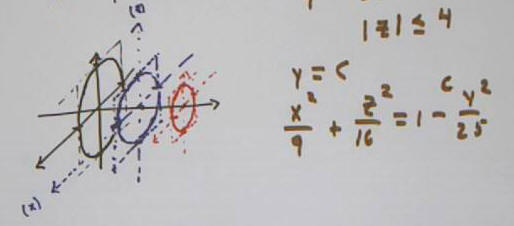
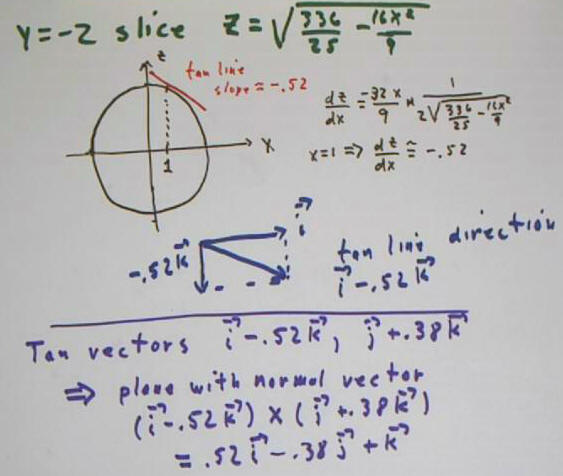
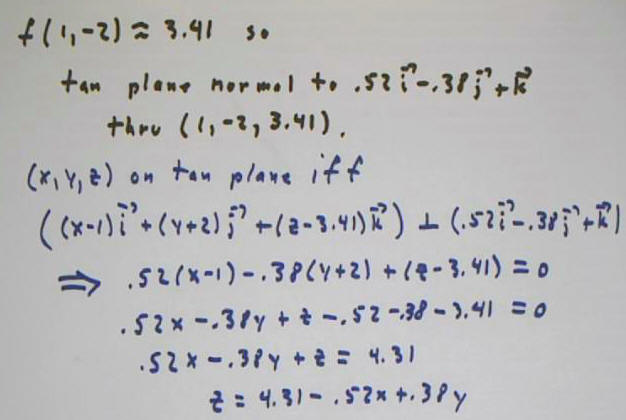
From x^2 / 9 + y^2 / 25 + z^2 / 16 = 1 we can solve so get z = +- sqrt( 16 - x^2 / 9 - y^2 / 25).

Plotting most of both

z = sqrt(16 - x^2 / 9 - y^2 / 25) and

z = -sqrt(16 - x^2 / 9 - y^2 / 25)

(leaving out some of the 'middle') we get the 'broken-eggshell' figure below.

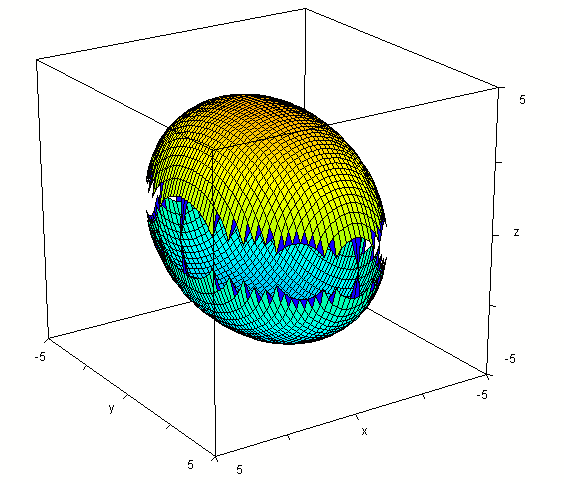
intersected with the plane z = 3 we get

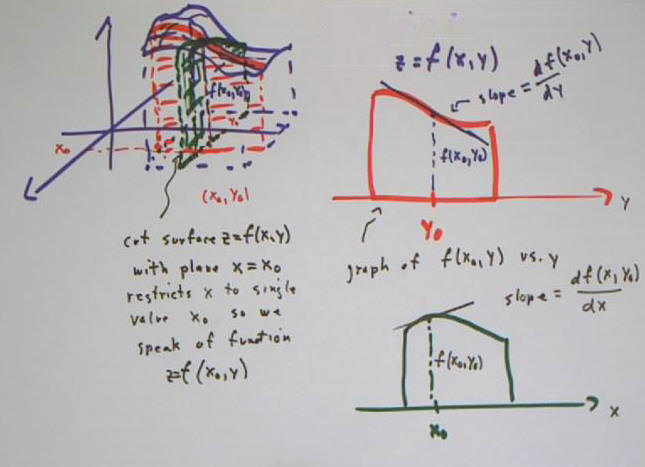
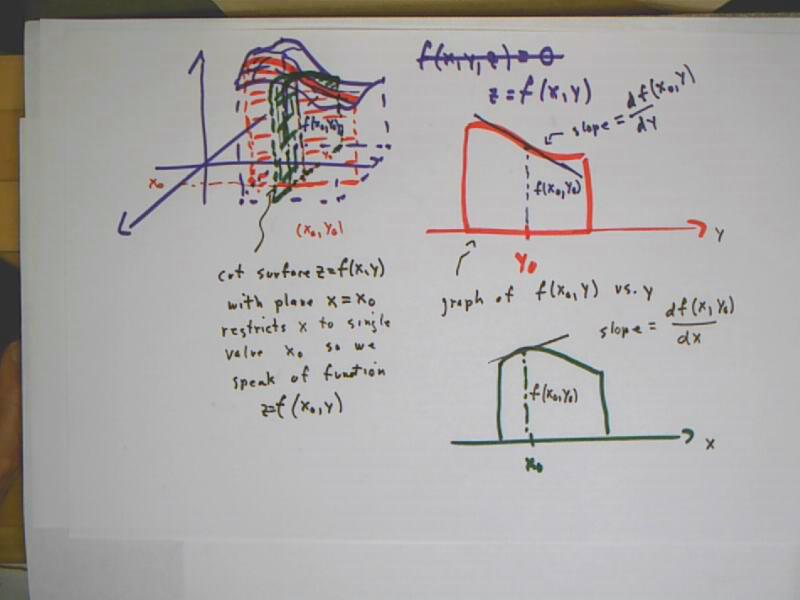
Intersecting the 'upper-half' function

z = f(x, y) = sqrt(16 - x^2 / 9 - y^2 / 25)

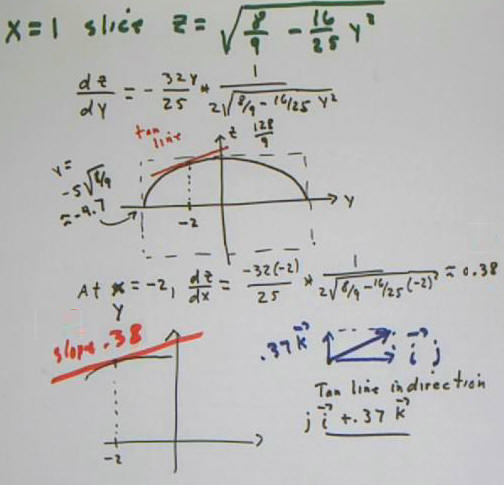
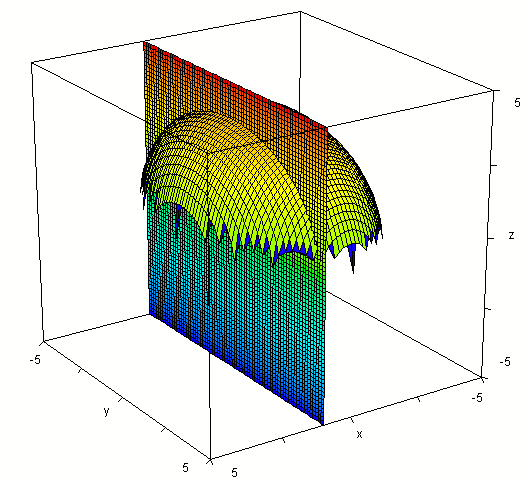
with the plane x = 1 we get the function

z = sqrt(16 - 1/9 - y^2 / 25),

which is an ellipse in the plane x = 1. 

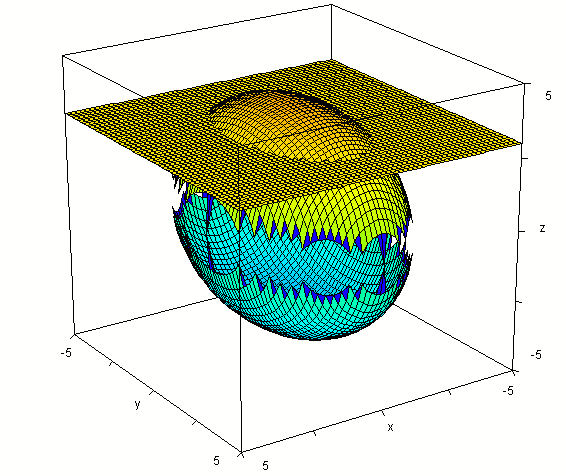
The intersection of the plane with the surface is seen below.

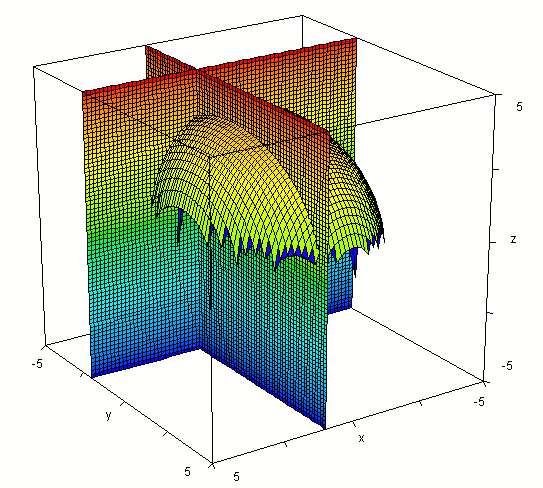
Intersecting the surface also with plane y = -2 we get the figure below.

In the plane y = -2 our f(x, y) function becomes

z = sqrt(16 - 4 / 25 - x^2 / 9 ),

which is an ellipse in x and z.

rotated a bit

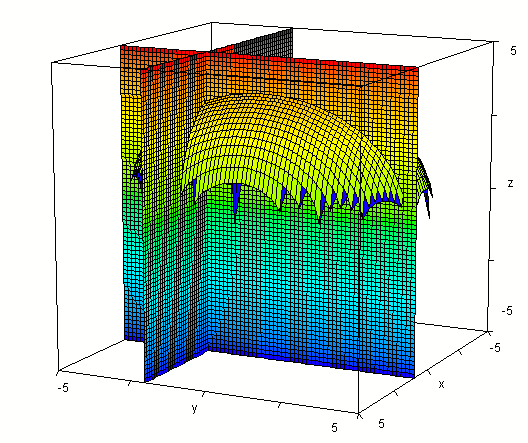
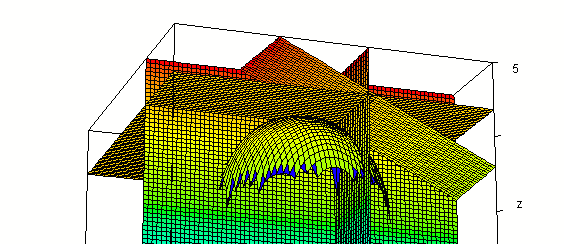
Evaluating f(x, y) at x = 1, y = -2 we get value 3.41.  So the point (1, -2, 3.41) should lie on our surface.

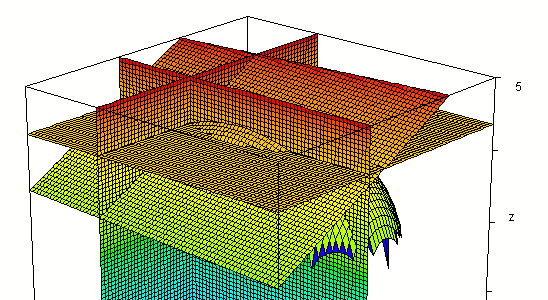
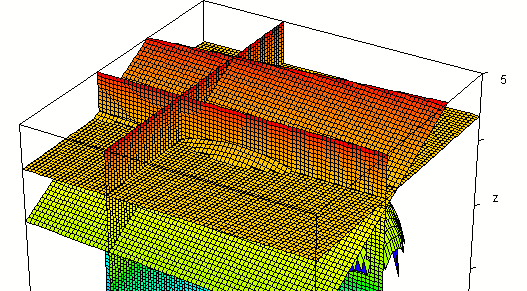
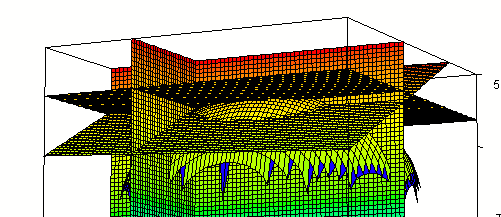
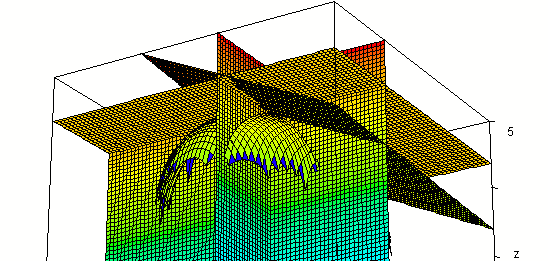
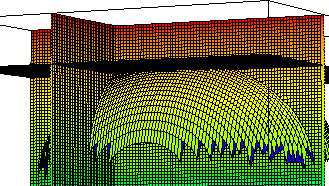
Intersecting our surface with plane z = 3.41 we get the figure below.  Note that the three planes and our surface appear to  come together at a point.  The three planes must intersect at (1, -2, 3.41) so this point does appear to lie on the surface.

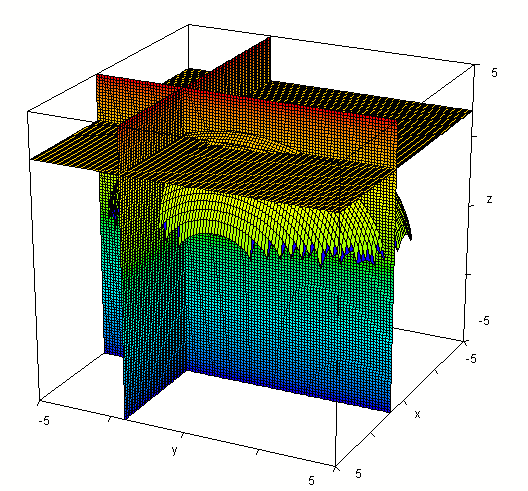
Additional perspective of the common intersection point, from a little ways below x-y plane

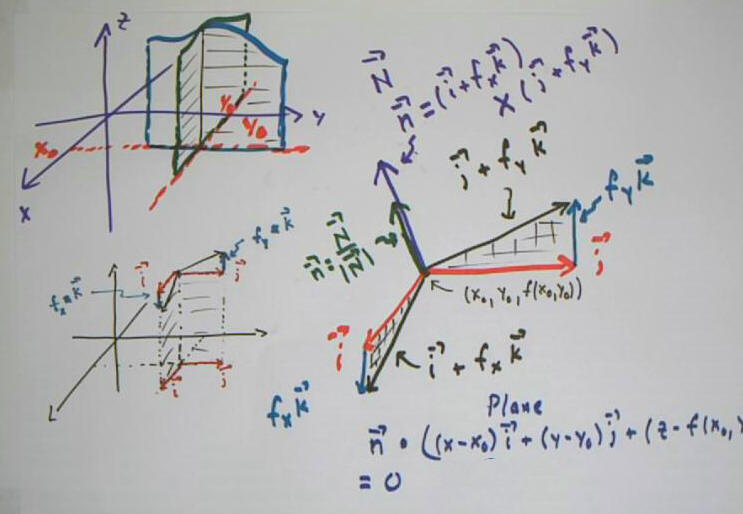
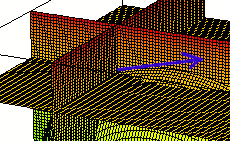
The 'blue' vector in the next figure is tangent to our surface at the common intersection point, along the curve formed where the surface intersects the plane x = 1.

If we take the y derivative of our f(x, y), and evaluate it for x = 1 and y = -2, we get about 0.05.  This is the slope of the curve formed in the plane x = 1, at the y = -2 point of that curve.  This indicates that the 'blue' vector in the figure is `j + .05 `k.

The 'blue' vector in the figure below is tangent at the common intersection point to the curve formed in the plane y = -2.

If we take the x derivative of our f(x, y), and evaluate it for x = 1 and y = -2, we get about -0.52.  This is the slope of the curve formed in the plane y = -2, at the x = 1 point of that curve.  This indicates that the 'blue' vector in the figure is `i + .52 `k.

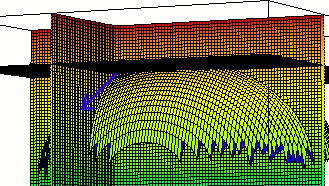
The cross product of our two 'blue' vectors is perpendicular to the plane formed by those vectors. 

It is easily seen that the cross product is -.52 `i - .05 `j + `k.

The intersection point is (1, -2, 3.41).

So the plane formed by the two vectors, at the point of common intersection, is

-.52 ( x - 1 ) - .05 ( y + 2) + 1 ( z - 3.41) = 0

Solving for z we have

z = -.52 x - .05 y + 3.83

The plane z = 3.83 - .52 x - .05 y intersected with the surface:

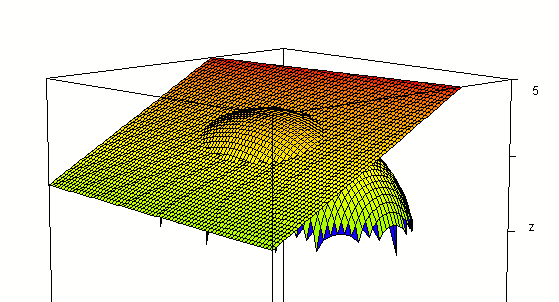
Adding the planes x = 1, y = -2, z = 3.41:

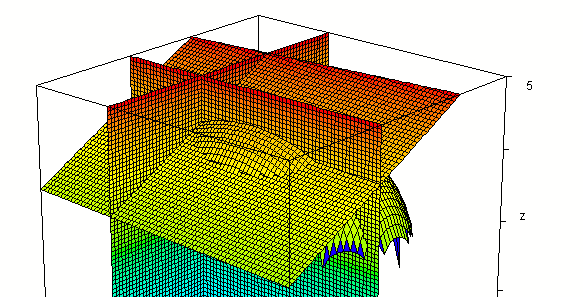
From various perspectives: