Section 9.7
In the x-y plane:
An ellipse has form (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1.
- This equation describes the ellipse inscribed in the rectangle centered at (h, k) with dimensions 2 a by 2 b, the former in the x direction and the latter in the y direction.
- The general form a^2 x^2 + c x + b^2 y^2 + d y + e = 0 can be converted to the given form by completing the squares on x and y.
A hyperbola has form (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1, or -(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1.
- Either equation describes a hyperbola asymptotic to the diagonals of the rectangle centered at (h, k) with dimensions 2 a by 2 b, the former in the x direction and the latter in the y direction.
- The vertices of the hyperbola are located on the rectangle, at either the points (h + a, k) and (h - a, k) or the points (h, k + b) and (h, k - b). Common sense (knowing that the negative of a square can't equal 1) determines which.
- The general forms are a^2 x^2 + c x - b^2 y^2 + d y + e = 0 and -a^2 x^2 + c x + b^2 y^2 + d y + e = 0. Either can be converted to the given form by completing the squares on x and y.
A parabola has basic form (y - k) = 1 / (4 p) * (x - h)^2 or (x - h) = 1 / (4 p) * ( y - k )^2.
- In either form, p is the displacement between vertex and focus, or between directrix and vertex.
- The former form has axis of symmetry parallel to the y axis, the latter has axis of symmetry parallel to the x axis.
- The general quadratic form is a x^2 + b x + c x^2 + d y + e = 0. If exactly one of a or d is zero the form yields a parabola and can be put into one of the given forms by completing the square.
There is much more to the properties of conic sections, which should have been covered thoroughly in Precalculus II, but the above will be sufficient for the most basic understanding of quadric surfaces.
A quadric surface is a three-dimensional surface, as defined in your text. The most important property of these surfaces for present applications is that the intersection of any quadric surface with a plane parallel to a given coordinate plane is a conic section, and the intersections of all planes parallel to the given coordinate plane are all conic sections of the same type.
When presented with a quadric surface, you need to first identify it.
A good first step is to identify the intersections of the surface with various planes. The following ideas will be useful:
- The x-y plane is just the plane z = 0.
- If you substitute z = 0 into the equation of a quadric surface, the resulting equation will be a conic section (either a parabola, a hyperbola or an ellipse) in the x-y plane.
- The planes z = 1, z = 2, z = 3, etc. are parallel to the x-y plane. If the x-y plane is regarded as horizontal and the z coordinate of a point represents how far that point is above or below the x-y plane, then the planes z = 1, z = 2 and z = 3 are horizontal planes that lie 1, 2 and 3 units above the x-y plane.
- The intersection of a quadric surface with one of these planes constitutes a 'horizontal slice' of the surface. By considering how the horizontal slices change as the z coordinate is increased or decreased, we can begin to form a picture of the surface.
- Every horizontal slice will either be a conic section, or will be 'empty' in the sense described below.
- To get the equation of the surface in the plane z =
1, just substitute z = 1 into the equation of the quadric surface, and you
will get either an equation of a conic section, or an equation that has no
solution. In the former case, just graph the conic section and you
will see the shape of the horizontal slice.
In the case where the equation has no solution, it means that the surface does not intersect the z = 1 plane (this could happen, for example, if the graph was a sphere or an ellipsoid that didn't extend as far as the z = 1 plane; it could happen if the graph was a paraboloid with a vertical axis of symmetry; you will recall that a parabola reaches a maximum or minimum at its vertex); it could happen in a number of other situations).
- To get the equation in the planes z = 2, z = 3, etc., just substitute each value in turn into the equation, see what conic section you get, and plot it. If the equation has no solution, then that particular plane does not intersect the surface.
- You can and should look at planes like z = -1, z = -2, etc..
- Then you should look plug in z = c, where c is regarded as a general constant, and consider how the value of c affects the parameters of the intersection (e.g., if the intersections are ellipses, consider how value of c influences the major and minor axes). Think about what happens when c increases, when it decreases, when it is positive, when it is negative, etc..
- The plane x = 0 is just the y-z coordinate plane. Plug x = 0 into the equation of the quadric surface, and you get the equation of the conic section in the y-z plane. Sketch this conic section in the y-z plane of your x-y-z coordinate system.
- The plane y = 0 is the x-z coordinate plane. Plug y = 0 into the equation of the quadric surface, find the conic section, then sketch this in the x-z plane of your 3-dimensional system.
- The planes x = 1, x = 2, x = -1, x = -2, etc., and the general plane x = c, are just vertical planes parallel to the y-z plane. By considering what happens to the conic section--how it changes in size with different values of c, or shrinks to a point, or ceases to exist, you get additional evidence about the surface. Sketching these shapes in the relevant planes enhances your understanding of the surface.
- The planes y = 1, y = 2, y = -1, y = -2, etc., and the general plane x = c, are just vertical planes parallel to the x-z plane. By considering what happens to the conic section--how it changes in size with different values of c, or shrinks to a point, or ceases to exist, you get additional evidence about the surface.
- More generally, you could intersect the surface with any plane. You would get a curve in 3-dimensional space, which you could represent parametrically. We will discuss this if and when the question comes up, but for now you should concentrate the idea of intersecting the surface with the various coordinate planes, and sketching the overall shape of the surface.
You might want to work through the problems below and see how they illustrate the ideas given above.
Consider the equation x^2 / 25 + y^2 / 4 - z^2 = 0.
Question: `q001. If z = 1, then what is the resulting equation in y and z? Put this equation into the standard form of a conic section, identify that conic section and sketch it.
Your solution:
Confidence rating:
Given Solution:
If z = 1 then the equation is x^2 / 25 + y^2 / 4 - 1 = 0,
which can be written
x^2 / 25 + y^2 / 4 = 1.
This is of the form x^2 / a^2 + y^2 / b^2 = 1, with a = 5 and b = 2.
This is an ellipse centered at the origin, with semi-major axis 5 in the x direction and semi-minor axis 2 in the y direction.
Its graph looks like this:
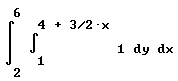
Self-critique (if necessary):
Self-critique rating:
Question: `q002. Answer the same for z = 2. Compare your sketch to your sketch for the first question.
Your solution:
Confidence rating:
Given Solution:
If z = 2 we get
x^2 / 25 + y^2 / 4 - 2^2 = 0, or
x^2 / 25 + y^2 / 4 = 4
which is put into standard form (which requires 1 on the right-hand side) by dividing both sides by 4. We obtain
x^2 / 100 + y^2 / 16 = 1,
which is an ellipse with semi-axes 10 and 4.
Its graph, and the graph of the ellipse from the preceding problem, looks like this:
The first ellipse is at z = 1, which is the plane parallel to the xy plane, lying 1 unit above the xy plane.
The second ellipse is at z = 2, which is the plane parallel to the xy plane, lying 2 units above the xy plane.
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Answer the same for z = 3, and make the same comparison.
Your solution:
Confidence rating:
Given Solution:
You will find that for z = 3 we get the ellipse
x^2 / 225 + y^2 / 36 = 1
with semi-axes 15 and 6.
A sketch of all three ellipses will show the ellipses growing linearly with the value of z, and you should visualize and attempt to sketch the ellipses on their respective planes z = 1, z = 2 and z = 3.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. If your sketches for the preceding three questions were made on transparent material and stacked, with their centers in a vertical line and the first being 1 unit above the tabletop, the second being 2 units above, and the third three units above, what 3-dimensional shape would they suggest?
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: `q005. What would the intersection of this 3-dimensional shape with the x-z plane look like?
Your solution:
Confidence rating:
Given Solution:
The plot would be a 3-dimensional surface consisting of a series of 'stacked' ellipses.
Plotted along with the plane z = 1 inside the rectangular region indicated below, in which x and y vary from -5 to 5 and z from 0 to 3, we see the elliptical z = 1 intersection.

Adding the z = 2 plane to the figure, we see part of the ellipse as it intersects that plane:

From the 'front' the figure looks like this:
From the 'side' the lower part looks like this:
Self-critique (if necessary):
Self-critique rating:
Question: `q006. What would the intersection of this 3-dimensional shape with the x-y plane look like?
Your solution:
Confidence rating:
Given Solution:
In the x-y plane our x and y values are both zero so our equation becomes jus
-z^2 = 0
with solution z = 0.
Thus when restricted to the x-y plane the surface consists of just the one point (0, 0, 0), the origin.
Self-critique (if necessary):
Self-critique rating:
Question: `q007. The plane x = 1 is parallel to the y-z plane, but passes through the x axis at x coordinate 1. What would the intersection of this plane with the surface look like?
Your solution:
Confidence rating:
Given Solution:
If x = 1 the surface becomes
1^2 / 25 + y^2 / 4 - z^2 = 0
so that
y^2 / 4 - z^2 = -1/25
or
z^2 - y^2 / 4 = 1/25.
This is a hyperbola which is asymptotic to the two lines z = y/2 and z = -y/2.
The vertices of this hyperbola are at the points
(0, 1/25) and (0, -1/25)
of the yz plane.
Self-critique (if necessary):
Self-critique rating:
Question: `q008. If y = 2, then what is the resulting equation in x and z? Put this equation into the standard form of a conic section, identify that conic section and sketch it.
Your solution:
Confidence rating:
Given Solution:
If y = 2 we get
x^2 / 25 + 2^2 / 4 - z^2 = 0
so that
x^2 / 25 - z^2 = -1
and
-x^2 / 25 + z^2 = 1.
This is a hyperbola with vertices at (0, 1) and (0, -1) in the x-z plane, asymptotic to the lines z = x / 5 and z = -x / 5 (the lines with slope 1/5 and -1/5, through the origin).
The figure below shows the upper half of the hyperbola:

Self-critique (if necessary):
Self-critique rating:
Question: `q009. Repeat the above for y = 4, then for y = 6.
Your solution:
Confidence rating:
Given Solution:
If y = 4 we get
x^2 / 25 - z^2 = -4
which rearranges to standard form
z^2 / 4 - x^2 / 100 = 1.
The vertices are at (0, 2) and (0, -2), and the asymptotes are still the lines z = 1/5 x and z -1/5 x.
For y = 6 the asymptotes are still the same, with vertices (0, 3) and (0, -3).
Self-critique (if necessary):
Self-critique rating:
Question: `q010. Your last three sketches describe the intersection of the surface x^2 / 25 + y^2 / 4 - z^2 = 0 with the planes y = 2, y = 4 and y = 6, each plane being parallel to the x-z plane and passing through the y axis at the indicated coordinate. Explain how your sketches are consistent with the surface as you described it, based on the three stacked graphs.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:
Question: `q011. Explain how the answers to the preceding questions would differ if the equation was x^2 / 25 + y^2 / 4 - z^2 = 2 instead of x^2 / 25 + y^2 / 4 - z^2 = 0.
Your solution:
Confidence rating:
Given Solution:
Self-critique (if necessary):
Self-critique rating:

