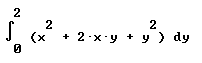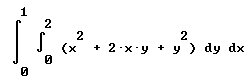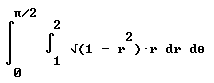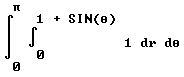• A dot B = a_1 b_1 + a_2 b_2 + a_3 b_3
• A dot B = || A || * || B || cos(theta).

cos(theta) = A dot B / || A || || B || so that

theta = arcCos( A dot B / || A || || B || ).

Two vectors are perpendicular to one another if the angle between them is 90 degrees.  The cosine of 90 degrees is zero, and if the cosine of an angle between 0 and 180 degrees is zero the angle is 90 degrees.  So two vectors are perpendicular if, and only if, their dot product is zero. 

If the dot product of two vectors is zero we say that the vectors are orthogonal.  In two or three dimensions, that means that the angle between the two vectors is 90 degrees.

Section 9.3

If you have worked through the recommended qa's on vectors, from Precalculus I, you should have little trouble with the following query questions:

1) Find v dot u when v =<1,-5,0> u =<0,-4,2>.

2) Find  v dot w when v = 4i + j and w =3i + 2k.

3) Determine whether v = 5i - 5j + 5k and w = 8i - 10j -2k are orthogonal.

4) Let v = 4i - 2j + k and w = -2i + j - k. Evaluate (v dot w) * w.

5) Find the angle between v = 2i +3 k and w = -j + 4k.

6) Find the scalar and vector projections of v = i - 2j onto w = j - 2k.

7) Find two distinct unit vectors orthogonal to both v = i + 2j -2k and w = i + j - 2k.

8) Find x so that v = 2i - xj + 3k and w = -2i + j + xk are orthogonal.

9) Give the direction cosines and direction angles of v = i - 4j.

10)  Let v = i - j + 4k and w = -i + 3j + 2k. Find cos(theta). Find s such that v is orthogonal to sv - w. Also find t such that v - tw is orthogonal to w

11) Find the work performed when a force F = (6/11)i - (2/11)j + (6/11)k is applied to an object moving along the line from P(3,5,-4) to Q(-4,-9,-11).

=====

Section 9.4

1) Find v X w when v = 10i - 2j + 4k and w =-i -(1/2)j - 3k. (Where X denotes the cross product)

2) Find v X w when v = sin(theta)i + cos(theta)j and w = -cos(theta)i + sin(theta)j  (theta is any angle).

3) Find sin(theta) where theta is the angle between v = -i + j and w = -i + j + 2k.

4) Find a unit vector which is orthogonal to both v = -i + 3j and w = i - j - k

5) Find a unit vector which is orthogonal to both v = 2i - j and w = 2j - k.

6) Find the area of the parallelogram determined by the vectors v = 4i + k and w = 4j - k.

7) Find the area of the triangle with vertices P(2,0,0), Q(1,1,-1), R(3,1,2).

8) Determine if each of the following products is a vector, scalar, or not defined at all. Explain why.  u X (v X w) , u dot (v dot w), (u X v) dot (w X r). 

9) Find the volume of the parallelepiped determined by u = i - j, v = i - 2k, and w = 4k

10) Find a number t such that the vectors -i - j, i - (1/2) j + (1/2)k and -2i -2j - 2tk all lie in the same plane.

11) u = 2i + 2j, v= i-(1/2)j+ (1/2)k, w = i. Compute (u X v) X w and u X (v X w). What does this say about the associativity of the cross product?

=====

Section 9.5

`q001.  Suppose x = 5 t and y = 3 t^2 - 6.  Solve x = 5 t for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

`q002.  Suppose x = 5 t^2 and y = 3 t^4 - 6.  Solve x = 5 t^2 for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

`q003.  Suppose x = 5 e^t and y = 3 e^(4t) - 6.  Solve x = e^t for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

Let `w = 2 `i - 4 `j + 3 `k, `v = 5 `i + 4 `j - 2 `k.  Let `r(t) = `w + t * `u.  Answer the following questions:

`q004.  Let P_0 be the terminal point of the `r vector when t = 0, and let P_2 be the terminal point when t = 2.  What is the vector from P_0 to P_2, and what is the unit vector in this direction?  What is the unit vector in the direction of `u?

`q005.  How does the solution to the preceding problem support the contention that all of the points 'traced out' by the tip of the `r(t) vector lie along a single straight line?

`q006.  What are the x, y and z coordinates of the tip of the `r(t) vector?  Write in the form x = ..., y = ..., z = ... where you fill in the expressions for ... .  Solve the resulting equation for t in terms of x.

`q007.  Plug the expression you got when you solved for t into the equation for y.  What do you get?  Do the same for the equation for z.  Using your results find the coordinates of the point (x, y, z) when x = 3.

`q008.  Solve each of the three equations (for x, y and z) for t.  Set the three expressions equal.  What set of equations do you get?

This ends the sequence of questions related to `w = 2 `i - 4 `j + 3 `k, `v = 5 `i + 4 `j - 2 `k.

`q009.  Suppose (x - 4) / 3 = (y + 2) / 6 = (z - 2) / 9.  What values of x, y and z make these three expressions all equal to zero?  If it is known that x = 7, what values of y and z make the other two equations true?

`q010.  Your solution to the preceding gives you the coordinates of two points.  If `w is the vector from the origin to the first, and `v the vector from the first point to the second, express `w and `u in terms of their `i, `j and `k components.

`q011.  If `w = x0 `i + y0 `j + z0 `k and `v = a `i + b `j + c `k, then what, in terms of x0, y0, z0, t, a, b and c, is the expression for the vector `w + t `v?  What are the expressions for the x, y and z components of this vector? 

`q012.  What do you get when you solve the three expressions each for t?  What do you get when you set the three expressions equal?

`q013.  Identify the `w and `v vectors for which the equations (x + 3) / 4 = (y - 2) / 5 = (z + 1) / 3 represent the line `w + s `v.

`q014.  Suppose one straight line is represented by parametric equations x(t) = 3 - 5 t, y(t) = 2 + 4 t and z(t) = -6 - 7 t, while another is represented by the equations x(s) = 2 - 3 s, y(s) = 3 + 6 s and z(s) = -3 - 2 s. 

If the two lines intersect, it means that for some value of t and some value of x, x(t) = x(s), while for the same values y(t) = y(s) and z(t) = z(s). 

• Show that if t = 1 and s = 2, it isn't so. 

Express the three given conditions as three simultaneous equations. 

• Do you expect the three equations to have a simultaneous solution?  Why or why not?

`q015.  If the three simultaneous equations in the preceding problem have a solution, find it.  If they don't, prove that they don't.

`q001.  Suppose x = 5 t and y = 3 t^2 - 6.  Solve x = 5 t for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

`q002.  Suppose x = 5 t^2 and y = 3 t^4 - 6.  Solve x = 5 t^2 for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

`q003.  Suppose x = 5 e^t and y = 3 e^(4t) - 6.  Solve x = e^t for t, then plug this expression in for t in the second equation.  Simplify the result.  What is your resulting formula for y in terms of x?

Let `s = 2 `i - 4 `j + 3 `k, `u = 5 `i + 4 `j - 2 `k.  Let `r(t) = `s + t * `u.  Answer the following questions:

`q004.  Let P_0 be the terminal point of the `r vector when t = 0, and let P_2 be the terminal point when t = 2.  What is the vector from P_0 to P_2, and what is the unit vector in this direction?  What is the unit vector in the direction of `u?

`q005.  How does the solution to the preceding problem support the contention that all of the points 'traced out' by the tip of the `r(t) vector lie along a single straight line?

`q006.  What are the x, y and z coordinates of the tip of the `r(t) vector?  Write in the form x = ..., y = ..., z = ... where you fill in the expressions for ... .  Solve the resulting equation for t in terms of x.

`q007.  Plug the expression you got when you solved for t into the equation for y.  What do you get?  Do the same for the equation for z.  Using your results find the coordinates of the point (x, y, z) when x = 3.

`q008.  Solve each of the three equations (for x, y and z) for t.  Set the three expressions equal.  What set of equations do you get?

`q009.  Suppose (x - 4) / 3 = (y + 2) / 6 = (z - 2) / 9.  What values of x, y and z make these three expressions all equal to zero?  If it is known that x = 7, what values of y and z make the other two equations true?

`q010.  Your solution to the preceding gives you the coordinates of two point

1) Find an explicit relationship between x and y by eliminating the parameter in the following equations: x = t, y = 2 - 3t. Sketch the corresponding curve for 0 <= t <= 1.

2) Find an explicit relationship between x and y by eliminating the parameter in the following equations: x = t^6, y = t^4 -3. Sketch the corresponding curve for -1 <= t <= sqrt(2).

3) Find an explicit relationship between x and y by eliminating the parameter in the following equations: x = e^-t, y = e^t. Sketch the corresponding curve for -inf <= t <= inf. (inf stands for infinity).

4) Find the parametric and symmetric equations for the line passing through the points (1,3,-2) and (-1,2,-1).

5) Find the parametric and symmetric equations for the line passing through the point (-1,-1,0) and parallel to the line (x-3)/4 = (y-1)/3 = (z+3)/2

6) Find the parametric form of the equation of the line passing through (-3,1,1) parallel to both the xz- and yz-planes.

7) Find the intersection of the line (x-1)/3 = (y+5)/2 = (z+6)/3 with each of the coordinate planes.

8) Find the intersection of the line represented by the parametric equations x = 3t + 4, y = 1 - 3t, z = 2t - 7 with each of the coordinate planes (or if it doesn't intersect one, specify which one).

9) Show whether the line represented by the parametric equations x = 2-t, y = 3t , z = 3 - 2t and the line represented by x = 5-t, y = -1-3t, z = -3 +4t intersect, are parallel, or if they are skew. If they intersect, give the point of intersection.

10) Show whether the line represented by the equation (x-1)/2 = (y-1)/-1 = (z-2)/1 and the line represented by (x+2)/3 = (y+3)/-1 = (z-4)/1 intersect, are parallel, or if they are skew. If they intersect, give the point of intersection.

11) Find a parametric equation of a circle of radius 4, centered at the origin, and oriented clockwise.

12) Determine whether the vector v = -(7/3)i - (4/3)j - k is orthogonal to the line passing through the points P(-2,2,7) and Q(1/2,-1/2,9/2).

13) What can be said about the lines (x-x0)/a1 = (y-y0)/b1 = (z-z0)/c1 and (x-x0)/a2 = (y-y0)/b2 = (z-z0)/c2 if  a1a2 + b1b2 + c1c2 = 0? 

=====

Section 9.6

Let P_0 = (2, 4, 5), P_1 = (4, 7, -2) and P_2 = (8, 1, -1).  Let `u be the vector from P_0 to P_1 and `w the vector from P_0 to P_2.

`q001.  Sketch the three points and the two vectors.

`q002.  Find the angle between `u and `w.  Does the angle make sense in terms of your sketch?

`q003.  Find a vector perpendicular to both `u and `w.  Call this vector the normal vector and denote it `n.

`q004.  Show that this vector `n is also perpendicular to the vector from P_1 to P_2. 

`q005.  Let P = (x, y, z) be the coordinates of a point in space.  What are the components of the vector from P_0 to P?

`q006.  Write the condition that the vector from P_0 to P be perpendicular to `n.  Express this condition as an equation.

`q007.  Show that the coordinates of P_0 satisfy this equation, and also that the coordinates of P_1, as well as the coordinates of P_2, also satisfy this equation.

`q008.  If you have had linear algebra, show the condition that (x, y, z) satisfies your equation is equivalent to the condition that the vector from P_0 to P = (x, y, z) is in the span of the vectors `u and `v.  This is also equivalent to the condition that `u and `v form a basis for the space of all such vectors.

`q009.  Write down the condition that the vector from (x0, y0, z0) to (x, y, z) is perpendicular to the vector `n = a `i + b `j + c `k, and simplify your condition into an equation.

`q010.  Find the coordinates of a point (x, y, z) which satisfy the condition that 2 x + 3 y - 5 z = 30. ...

1) Write the equation of the plane 3(x-2) - 2(y-1) - 3(z-5) = 0 in standard form.

2) Find the equation of the plane containing the point P(-1,3,2) and having normal vector N = 3j - 1k.

3) Find the equation of the plane containing the point P(0,0,0) and having normal vector N = i.

4) Find two unit vectors perpendicular to the plane x + 3y - 4z = 2.

5) Find the distance between the point P(-1,1,-1) and the plane 2x - 3y + z = 4.

6) Find the distance between the point (-1,2,1) and the plane which passes through the points (0,0,0) , (2,4,8) and (2,1,-1).

7) Find the distance between the point (-1,2,1) and the plane which contains the point (3,3,-2) and is normal to the vector N = -2i + j + 3k.

8) Find the distance between the point P(1,1,1) and the line (x-2)/3 = (y-1)/2 = (z-3)/4.

9) Find the distance between the lines (x+1)/-2 = (y+2)-2 = (z+1)/-1 and (x-4)/5 = (y+1)/2 = (z-1)/3

10) Find the equation of the sphere with center C(-2,7,1) and tangent the the plane x + 4y - 2z = 10.

11) Find an equation for the plane that contains the point (1,1,-2) and is orthogonal to the line (x-3)/2 = (y+1)/4 = (z-3)/2.

12) The angle between two planes is defined to be the acute angle between the normal vectors of the planes. Find the angle between the planes x - y + 3z = 2 and 2x + y - z = -2. Round the angle to the nearest degree.

13) Show that the angle between the planes (A1)x + (B1)y + (C1)z + D1 = 0 and (A2)x + (B2)y + (C2)z + D2 = 0 is pi/2 if and only if (A1)A2+ (B1)B2 + (C1)C2 = 0. (In case you don't remember, proving an "if and only if" statement means start with the statement on the left and get to the one on the right and then start with the one on the right and get to the left.)

=====

Section 9.7

In the x-y plane:

An ellipse has form (x - h)^2 / a^2 + (y - k)^2 / b^2 = 1.

• This equation describes the ellipse inscribed in the rectangle centered at (h, k) with dimensions 2 a by 2 b, the former in the x direction and the latter in the y direction.
• The general form a^2 x^2 + c x + b^2 y^2 + d y + e = 0 can be converted to the given form by completing the squares on x and y.

A hyperbola has form (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1, or -(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1.

• Either equation describes a hyperbola asymptotic to the diagonals of the rectangle centered at (h, k) with dimensions 2 a by 2 b, the former in the x direction and the latter in the y direction.
• The vertices of the hyperbola are located on the rectangle, at either the points (h + a, k) and (h - a, k) or the points (h, k + b) and (h, k - b).  Common sense (knowing that the negative of a square can't equal 1) determines which.
• The general forms are a^2 x^2 + c x - b^2 y^2 + d y + e = 0 and -a^2 x^2 + c x + b^2 y^2 + d y + e = 0.  Either can be converted to the given form by completing the squares on x and y.

A parabola has basic form (y - k) = 1 / (4 p) * (x - h)^2 or (x - h) = 1 / (4 p) * ( y - k )^2.

• In either form, p is the displacement between vertex and focus, or between directrix and vertex.
• The former form has axis of symmetry parallel to the y axis, the latter has axis of symmetry parallel to the x axis.
• The general quadratic form is a x^2 + b x + c x^2 + d y + e = 0.  If exactly one of a or d is zero the form yields a parabola and can be put into one of the given forms by completing the square.

There is much more to the properties of conic sections, which should have been covered thoroughly in Precalculus II, but the above will be sufficient for the most basic understanding of quadric surfaces. 

A quadric surface is a three-dimensional surface, as defined in your text.  The most important property of these surfaces for present applications is that the intersection of any quadric surface with a plane parallel to a given coordinate plane is a conic section, and the intersections of all planes parallel to the given coordinate plane are all conic sections of the same type.

When presented with a quadric surface, you need to first identify it. 

A good first step is to identify the intersections of the surface with various planes.  The following ideas will be useful:

• The x-y plane is just the plane z = 0. 
• If you substitute z = 0 into the equation of a quadric surface, the resulting equation will be a conic section (either a parabola, a hyperbola or an ellipse) in the x-y plane.

• The planes z = 1, z = 2, z = 3, etc. are parallel to the x-y plane.  If the x-y plane is regarded as horizontal and the z coordinate of a point represents how far that point is above or below the x-y plane, then the planes z = 1, z = 2 and z = 3 are horizontal planes that lie 1, 2 and 3 units above the x-y plane.
• The intersection of a quadric surface with one of these planes constitutes a 'horizontal slice' of the surface.  By considering how the horizontal slices change as the z coordinate is increased or decreased, we can begin to form a picture of the surface.
• Every horizontal slice will either be a conic section, or will be 'empty' in the sense described below.

• To get the equation of the surface in the plane z = 1, just substitute z = 1 into the equation of the quadric surface, and you will get either an equation of a conic section, or an equation that has no solution.  In the former case, just graph the conic section and you will see the shape of the horizontal slice. 

  In the case where the equation has no solution, it means that the surface does not intersect the z = 1 plane (this could happen, for example, if the graph was a sphere or an ellipsoid that didn't extend as far as the z = 1 plane; it could happen if the graph was a paraboloid with a vertical axis of symmetry; you will recall that a parabola reaches a maximum or minimum at its vertex); it could happen in a number of other situations). 

• To get the equation in the planes z = 2, z = 3, etc., just substitute each value in turn into the equation, see what conic section you get, and plot it.  If the equation has no solution, then that particular plane does not intersect the surface.
• You can and should look at planes like z = -1, z = -2, etc..

• Then you should look plug in z = c, where c is regarded as a general constant, and consider how the value of c affects the parameters of the intersection (e.g., if the intersections are ellipses, consider how value of c influences the major and minor axes).  Think about what happens when c increases, when it decreases, when it is positive, when it is negative, etc..

• The plane x = 0 is just the y-z coordinate plane.  Plug x = 0 into the equation of the quadric surface, and you get the equation of the conic section in the y-z plane.  Sketch this conic section in the y-z plane of your x-y-z coordinate system.
• The plane y = 0 is the x-z coordinate plane.  Plug y = 0 into the equation of the quadric surface, find the conic section, then sketch this in the x-z plane of your 3-dimensional system.

• The planes x = 1, x = 2, x = -1, x = -2, etc., and the general plane x = c, are just vertical planes parallel to the y-z plane.  By considering what happens to the conic section--how it changes in size with different values of c, or shrinks to a point, or ceases to exist, you get additional evidence about the surface.  Sketching these shapes in the relevant planes enhances your understanding of the surface.
•  The planes y = 1, y = 2, y = -1, y = -2, etc., and the general plane x = c, are just vertical planes parallel to the x-z plane.  By considering what happens to the conic section--how it changes in size with different values of c, or shrinks to a point, or ceases to exist, you get additional evidence about the surface.

• More generally, you could intersect the surface with any plane.  You would get a curve in 3-dimensional space, which you could represent parametrically.  We will discuss this if and when the question comes up, but for now you should concentrate the idea of intersecting the surface with the various coordinate planes, and sketching the overall shape of the surface.

You might want to work through the problems below and see how they illustrate the ideas given above.

Consider the equation x^2 / 25 + y^2 / 4 - z^2 = 0. 

`q001.  If z = 1, then what is the resulting equation in y and z?  Put this equation into the standard form of a conic section, identify that conic section and sketch it.

`q002.  Answer the same for z = 2.  Compare your sketch to your sketch for the first question.

`q003.  Answer the same for z = 3, and make the same comparison.

`q004.  If your sketches for the preceding three questions were made on transparent material and stacked, with their centers in a vertical line and the first being 1 unit above the tabletop, the second being 2 units above, and the third three units above, what 3-dimensional shape would they suggest?

`q005.  What would the intersection of this 3-dimensional shape with the x-z plane look like?

`q006.  What would the intersection of this 3-dimensional shape with the x-y plane look like?

`q007.  The plane x = 1 is parallel to the y-z plane, but passes through the x axis at x coordinate 1.  What would the intersection of this plane with the surface look like?

`q008.  If y = 2, then what is the resulting equation in x and z?    Put this equation into the standard form of a conic section, identify that conic section and sketch it.

`q009.  Repeat the above for y = 4, then for y = 6. 

`q010.  Your last three sketches describe the intersection of the surface x^2 / 25 + y^2 / 4 - z^2 = 0 with the planes y = 2, y = 4 and y = 6, each plane being parallel to the x-z plane and passing through the y axis at the indicated coordinate.  Explain how your sketches are consistent with the surface as you described it, based on the three stacked graphs.

`q011.  Explain how the answers to the preceding questions would differ if the equation was x^2 / 25 + y^2 / 4 - z^2 = 2 instead of x^2 / 25 + y^2 / 4 - z^2 = 0.

1) Identify the quadric surface (x^2)/16 + (y^2)/1 = (z^2)/9

2) Identify the quadric surface 4y = (z^2)/4 - (x^2)/9.

3) Identify the quadric surface given by the equation (x^2)/9 - (y^2)/4 - (z^2)/4 = 1. Describe the traces in planes parallel to the coordinate planes (and sketch the graph).

4) Identify the quadric surface given by the equation 8z^2 = (1/8) + (x^2)/9 + (y^2). Describe the traces in planes parallel to the coordinate planes (and sketch the graph).

5) For the surface given by the equation y^2 - 4x^2 + 16z^2 = 16. Give the axis of symmetry (either x- or y-axis) and identify the surface (and sketch the surface).

6) Describe the quadric surface given by the equation 4z = (2x + 4 )^2 + ((2y -1)^2)/9 + 3.

7) Describe the quadric surface given by the equation ((x-3)^2)/2 - ((y-1)^2)/4 - (z^2-2)/9 = 4.

8) Describe the curve intersection of the two quadric surfaces 4z = (y^2)/9 - (x^2)/16 and (x^2)/4 + 2(y^2) - 4(z^2)/3 = 1.

9) What is the intersection of the surfaces z = x^2 + y^2 and y = x?

10) The line (x = 1 + t , y = 2 - t , z = (1/3)t ) intersects the hyperboloid 4z^2/9 - 4x^2 + y^2/4 =4 at two points. Find the distance between these two points.

=====

Section 10.1

1) Find the domain of the vector function F(t) =  (sin t)i +(tan t)j - (sec t)k

2) Find the domain of F(t) X G(t) when F(t) = t^2 i - (t+2)j + (t-1)k and G(t) = (1/(t+2))i + (t-5)j + sqrt(t) k.

3) Describe the graph of G(t) = (e^t) i + (t^2) k in R^3

4) Describe the graph of G(t) = (sin t)i + (cos t)j + (4/3)k

5) Given F(t)= ti - 5tj +(t^2)k and H(t) = (cos (1-t))i + (e^t)k, find t^2( F(t)) - 3H(t).

6) Given F(t)= ti - 3tj +(2t^2)k and H(t) = (tan t)i + (e^-t)j, find F(t) X G(t)

7) Given F(t)= (t)i - 5(e^t)j +(t^3)k, G(t) = ti - (1/t)k and H(t) = (t*sin t)i + (e^-t)j, find H(t) dot [G(t) X F(t)]

8) Find a vector function F whose graph is the curve given by the equation x/5 = (y-3)/6 = (z+2)/4.

9) Find parametric equations for the curve of the intersection (or show that the surfaces do not intersect) for the elliptical cylinder x^2 + 3y^2 =9 and the parabolic cylinder 4z = 2x^2 - 1.

10) Find the limit as t -> 2 of ((t^4-2)/(t-2))i + ((t^2-4)/(t^2-2t))j + ((t^2 + 3)e^(t-2))k.

11) Determine all values of t for which G(t) = u/(||u||) is defined, where u = (t^2)i + sqrt(-t)j.

12) How many revolutions are made by the circular helix R(t) = (sin t)i + (cos t)j + (3/4)tk in a vertical distance of 12 units.

13) Define `dH = H(t + `dt) - H(t) where `dt is a small change in the parameter t. Show that `d(F X G)(t) = F(t + `dt) X `dG(t) + `dF(t) X G(t). (`d stands for the capital Greek letter Delta. If you need help look at the hint in the book for this problem, it will give you a very good start.)

=====

Section 10.2

The velocity vector corresponding to position vector `R(t) = x(t) `i + y(t) `j + z(t) `k is the derivative `v(t) = `R ' (t) = x ' (t) `i + y ' (t) `j + z ' (t) `k, and the acceleration vector is `a(t) = `v ' (t)  = `R '' (t) = x '' (t) `i + y ''(t) `j + z '' (t) `k.

The unit tangent vector is the vector function `T(t), equal at every instant to the unit vector in the direction of the velocity `v(t).

The acceleration vector has components `a_T(t) in the direction of the unit tangent vector, and `a_N(t) = `a(t) - `a_T(t) in the direction perpendicular to the unit tangent vector. 

The unit normal vector is the unit vector in the direction of `a_N(t), and is perpendicular to the unit tangent vector.

The direction of the derivative `T ' (t) of the unit tangent vector is the same as that of the unit normal vector.

The unit binormal vector `B(t) is the cross product of the unit tangent and unit normal vectors.

Note that ` in front of a symbol indicates that the symbol is a vector.  The only exception: `d means 'Delta'.  I will eventually search-replace the document to convert the notation to boldface.

If `R(t) = sin(t) `i + cos(`t) j + t `k then:

`q001.  What are the associated velocity and acceleration vectors?

Given Solution:

`v(t) = `R ' (t) = -cos(t) `i + sin(t) `j + `k

`a(t) = `v ' (t) = `r '' (t) = sin(t) `i + cos(t) `j

`q002.  What is the function describing the unit tangent vector?

Divide `v(t) by || `v(t) || and simplify

`q003.  What is the component of the acceleration vector in the direction of the unit tangent vector?

The component is denoted `a_T (t) .  The desired component is the projection of `a(t) on `T(t).

`q004.  What is the component of the acceleration vector in the direction perpendicular to the unit tangent vector?

Subtract the component `a_T(t) from `a(t).

`q005.  What is the normal component of the acceleration?

This is the component perpendicular to the unit tangent vector.

`q006.  Show that the normal component of the acceleration is perpendicular to the tangential component.

Two vectors are perpendicular if their dot product is zero.

`q007.  Show that the direction of the derivative of the unit tangent vector is the same as that of the unit normal vector.

Two vectors are parallel if the cosine of the angle between them is zero.  How therefore can to test to see if the vectors are parallel?  What further test allows us to determine if they are in the same direction, vs. in the opposite directions.

`q008.  Find the unit normal vector.

You have at least one vector in the normal direction (in fact in the preceding questions you have found two).  Use either to find the unit normal.

`q009.  Find the unit binormal vector.

You should have the unit normal and unit tangent.  Use them to easily find the unit binormal.  How do you know that your result is a unit vector?

`q009.  What difference would it make in the above results if the function was `R(t) = sin(t^2) `i + cos(t^2) `j + t `k?

`q010.  What difference would it make in the above results if the function was `R(t) = sin(t^2) `i + cos(t^2) `j + t^2 `k?

1) Find F' for F(s) = ((s+1)i + (s^3)j - (s^2)k) + ((s^2)i + sj + (3s+3)k).

2) Find F' for F(t) = (cos t)(3i + (tan t)j + 3(sec t)k)

3) Find both F' and F'' for F(t) = (4sin^2 t)i + (9cos^2 t)j + tk

4) Differentiate g(x) = <sin x, (1/x) ,-x> dot <csc x, -(x^2), 3x> with respect to x.

5) Given the position vector of a particle R(t) = (cos t)i + tj + (4 sin t)k, find the particle's velocity and acceleration vectors and then find the speed and direction of the particle at t = pi/2.

6) Find the tangent vector to the graph of F(t) = (-ti + (t^2)j - (t^3)k)/(1- t) at t = 0 and at t =2.

7) Find parametric equations for the tangent line to the graph of the vector function F(t) = <cos t, sin t, e^t> at the point corresponding to t = pi.

8) Find Int(<sin t, cos t, t^2> dt) (Where Int( f(t) dt) is the integral of f with respect to t)

9) Find Int((e^t)*<t,4t^2,sin t> dt)

10) Find the position vector R(t) given the velocity vector v(t) = 3(t^2)i + (e^t)j + sqrt(t/2)k and the initial position R(0) = 3i - 2j - k.

11) Find the velocity and position vectors given the acceleration vector `A(t) = 4(t^2)i - 2 sqrt(t) j + 5(e^3t)k, initial position R(0) = 2i + j -3k and initial velocity v(0) = 4i + j + 2k.

12) Find a value of a such that the following equality holds.

• Int( (t(sqrt(1+t^2)) i + (1/(1+t^2))j dt, 0, a) = (2sqrt(2) - 1)i - pi/4 j.

Notation:  The expression (Int(f(t) dt, a, b) represents the integral of f(t) with respect to t from a to b).

13) F(t) = e^(-kt)i + e^(kt)k. Show that F and F'' are parallel.

14) If G = F dot (F' X F'') then what is G' and what does it mean?

=====

Section 10.3

If the velocity function for a projectile is `v(t) = 10 `i + (20 - 9.8 t) `j, then:

`q001.  What is its position function `R(t), and what is its acceleration function `a(t)?

Velocity is the derivative of position, so you need an antiderivative.

`q002.  What is its position function if its t = 0 position is `R(0) = 0 `i + 10 `j?

Your antiderivatives contain integration constants.  From the given conditions you can evaluate those constants.

`q003.  At what instant is the `j component of the position function equal to 20?

`q004.  At what instant is the `i component of the position equal to 20, and at that instant what is the `j component of its position?

`q005.  At what instant is the `j component of its position maximized?

A function is maximized or minimized at a critical point.  A first- or second-derivative test can check whether a critical point gives us a max or a min, or perhaps an inflection point.

`q006.  At what instant is the `j component of its position zero, and at that instant what is the `i component of its position?

The quadratic formula might be useful.

`q007.  At what instant is the angle between `R(t) and the `i vector equal to 70 degrees? Does this occur at only one instant?

Use the dot product to get an expression for the angle.

`q008.  Give a set of parametric equations x = x(t) and y = y(t) that describe the position of the projectile.  Eliminate the variable t, and solve for y in terms of x.  What kind of equation do you get?  Describe its graph.

The position is x(t) `i + y(t) `j.  You figured out the position function in the second problem.

You eliminate the variable by solving for either x or y in terms of t, then substituting in the equation for y or x (depending on whether you solve the x or the y equation for t).

We now consider the representation of position and velocity in polar coordinates:

At any instant a moving carries along with it its unit tangent, unit normal and unit binormal vectors, giving it sort of a moving and changing coordinate system.

At any point P of the plane, we can define a different coordinate system, not related to the motion of the object.  This system consists of two perpendicular unit vectors `u_r and `u_theta, where `u_r is the unit vector in the direction of the `r vector (the vector from the origin to the point P), and `u_theta is the unit vector perpendicular to `u_r which is oriented in the direction of increasing theta.

If the polar coordinates of the point P are (r, theta), then the `r vector can be expressed in rectangular coordinates as `r = r cos(theta) `i + r sin(theta) `j.  The unit vector in the direction of `r is therefore `u_r = `r / || `r || =  (r cos(theta) `i + r sin(theta) `j) / r = cos(theta) `i + sin(theta) `j.  The unit vector perpendicular to `u_r is either sin(theta) `i - cos(theta)`j or -sin(theta) `i + cos(`theta) `j.  The latter is in the direction of increasing theta.

Thus `u_r = cos(theta) `i + sin(theta) `j, and `u_theta = -sin(theta) `i + cos(theta) `j.

Now if the polar coordinate r is changing at rate dr/dt, it follows that the component of the velocity vector in the direction of `u_r is just dr/dt.

If the angle theta changes, the corresponding change in the position of the point depends on how far it is from the pole.  The change in position resulting from a change `dTheta in the angle theta, at a point r units from the pole, is easily seen to be r * `dTheta. 

Thus if the polar coordinate theta is changing at rate dTheta / dt, the component of the change in position in the direction of `u_Theta is r * (dTheta / dt).

If r is changing at rate dr/dt, and theta is changing at rate dTheta/dt, then the rate at which position changes is therefore

rate of change of position with respect to t = d`r /dt = `v(t) = r dr/dt `u_r + r * dTheta/dt `u_theta.

`q009.  Sketch the point whose rectangular coordinates are (3, 4).  Sketch the vector `r from the origin to this point.  Without calculating anything sketch the unit vectors `u_r (in the direction of `r) and `u_theta (perpendicular to `r and in the direction of increasing theta), using (3, 4) as the initial point of both.  Sketch the x and y components of  `u_r and of `u_theta.  Estimate those components.

What are the polar coordinates of the point whose rectangular coordinates are (3, 4)?  What therefore are the rectangular coordinates of the vector `u_r?  What are the rectangular coordinates of the vector `u_theta?  How do your calculated components compare?

`q010.  If the polar coordinates of a moving point are r = t / 3 and theta = 2 pi t, then what is the corresponding velocity vector function `v(t), in terms of the unit vectors `u_r and `u_theta?

1) Find the time of flight t_f (to the nearest tenth of a second) and the range Rf (to the nearest unit) of a projectile fired (in a vaccum) from ground level at `alpha = 60 degrees and v0 = 75 ft/s. Assume that g = 32 ft/s^2.

2) Find the time of flight Tf (to the nearest tenth of a second) and the range Rf (to the nearest unit) of a projectile fired (in a vaccum) from ground level at `alpha = 65.54 degrees and v0 = 19.07 m/s. Assume that g = 9.8 m/s^2.

3) An object is moving along the curve x = -cos t , y = sin t in the plane. Find its velocity and acceleration in terms of the unit polar vectors u_r and u_theta.

4) An object is moving along the curve r = 1/(1 - sin(theta)), theta = t - pi/2.  Find its velocity and acceleration in terms of the unit polar vectors u_r and u_theta.

5) A baseball hit at a 35 degree angle from 3.5ft above the ground just goes over the 8ft-fence 400ft from home plate. How fast was the ball travelling, and how long did it take the ball to reach the wall?

6) If a shotputter throws a shot from a height of 5.5t and an angle of 53 degrees with initial speed 28 ft/s. What is the horizontal distance of the throw?

7) A .25lb paddleball attached to a string is swung in a circular path with a 1.5ft radius. If the string will break under a force of 3lb, find the maximum speed the ball can attain withouth breaking the string

8) A child running along level ground at the top of a 40ft high vertical cliff at a speed of 15ft/s, throws a rock over the cliff into the sea below. If the rock is released 10 ft from the edge and at an angle of 45degrees, how long does it take the rock to hit the water and how far away from the base of the cliff does it hit?

9) A particle moves along the polar path (r, theta) where r(t) = 4 - 2cost and theta(t) = t^2. Find V(t) and A(t) in terms of u_r and u_theta.

10) **A gun is fired with muzzle speed 700ft/s at an angle of 20degrees. It overshoots the target by 60 ft. If the target is moving away from the fun at a constant speed of 15ft/s and the gunner takes 30 seconds to reload, at what angle should the second shot be fired with the same muzzle speed?

=====

The unit tangent vector is the unit vector in the direction of the velocity.

The tangential component of the acceleration is the projection of the acceleration vector on the unit tangent vector.

The normal component of the acceleration is the acceleration, minus its component in the direction of the unit tangent vector. 

The unit normal vector is the unit vector in the direction of the normal component of the acceleration vector.  A vector parallel to the normal vector can also be obtained by taking the derivative of the unit tangent vector.

The unit binormal vector is the cross product of the unit tangent and unit normal vectors.

The speed of a point whose position function is R(t) is the magnitude of the velocity vector.

Section 10.4

... A point moves around a circle of radius A at constant speed v.  If the radial line vector from the center of the circle to the point

The position vector of a moving point is `R(t) = A cos(omega * t) `i + A sin(omega * t) `j.  For this position function:

`q001.  Sketch the path of the point.

`q002.  What are the corresponding velocity and acceleration vectors?

`q003.  What is the speed of the point and what is the magnitude of the acceleration?  Does either change with respect to t?

`q004.  What is the angle between `R(t) and the velocity vector, and what is the angle between the velocity vector and the acceleration vector? 

`q005.  Sketch the position vector, the velocity vector and the acceleration vector at the instant when omega * t = pi / 6.

`q006.  Let v be the speed of the point and r the radius of the circle.  What is the expression for the magnitude of the acceleration in terms of v and r?

`q007.  If another point is moving around a different circle at a different constant speed v, then if the magnitude of the acceleration of that point is a_cent, what is the radius of the circle?

The position vector of a moving point is `R(t) = A cos(omega * t^2) `i + A sin(omega * t^2) `j. 

`q008.  Sketch the path of the point.

`q009.  Find the acceleration and velocity vectors, and the magnitudes of both.  Does either change with respect to t?

`q010.  Find the components of the acceleration in the direction of the velocity, and perpendicular to the direction of the velocity.  Find the magnitudes of both components of the acceleration.

`q011.  If an object was moving around a circle with constant speed equal to that of this particle, with acceleration toward the center of the circle equal in magnitude to the perpendicular component of the acceleration, what would be the expression for the radius of that circle?  Of course we know that the circle in this example has radius A, but don't use that knowledge in your solution. 

`q012.  For any position function `R(t), we can follow the same procedure to find the radius of a hypothetical circle.

At any t, we can sketch the osculating circle, which is a circle whose radius is given by the expression found in the preceding question, subject to the condition that the direction of the radial vector (i.e., the vector from the center of that circle to the moving point) is in the direction opposite the unit normal.  This is easily understood from a sketch.  The center and radius of the osculating circle. The path of the particle at The curvature of the path at that instant is equal to the reciprocal of the radius of the osculating circle. 

The osculating circle is the circle of the radius you found in the preceding, whose center

`q013.  The curvature of the path of the particle is equal to the reciprocal of the radius of the osculating circle.

1) Find T(t) and N(t) when R(t) =( t^2 cost) i + (t^2 sint) j.

2) Find T(t) and N(t) when R(t) = (e^-2t cost)i + (e^-2t sint )j + e^-2t.

3) Find the length of R(t) = (7/3)t^3i + 2t^3j + 4t^3k on the interval [0,1].

4) Find the curvature of the plane curve y = sin (-3x) at x = pi/2.

5) Express R(t)= <sin2t, cos2t> in terms of the arc length parameter s measured from the point t = 0 in the direction of increasing t.

6) Let u and v be constant nonzero vectors. Show that the line given by R(t) = u + tv has curvature 0 at each point.

7) Let C be the curve given by R(t) = (1-cos t)i + (t-sin t)j + (4sin(t/2))k

• Find the unit tangent vector T(t) to C
• Find dT/ds and the curvature k(t)

8) Find the maximum curvature for the curve y = e^3x.

9) Find the curvature of R(t) = (3t-3sin t)i + (cost)j + 3k using both cross derivative form and two derivatives form.

10) Find the curvature of r = 1 + sin(theta) for theta in [0,2pi] using the polar form.

11) Let C be a smooth curve in R^2 described by the parametric equations x = x(t) and y = y(t).

• **Derive the parametric form of the curvature using a form which has already been proven in the text. (Hint: How else can you think of parametric equations for a function?)
• Find the curvature of the curve described by x = 1 - sin t, y = 7 + cos t.

12)** If T and N are the unit tangent and normal vectors on the trajectory of a moving body, we can define B = T X N to be the unit binormal vector. A coordinate system with three planes can be made at each point with these vectors since they are mutually orthogonal.

• Show that T is orthogonal to dB/ds (Hint: Differentiate B dot T)
• Show that B is orthogonal to dB/ds (Hint: Differentiate B dot B)
• Show that dB/ds = -(tau)N for some constant tau. (We call the constant tau the torsion of the trajectory)
• **Prove the Frenet-Serret formulas: (dT/ds = kN, dN/ds = -kT + tauB, dB/ds = -tauN). Where k is the curvature and tau = tau(s) is a scalar function.

=====

Section 10.5

1) Find the tangential and normal components of an object's acceleration given its position vector R(t) = <2 cos t, 5 sin t>.

2) Find the tangential and normal components of an object's acceleration which has the position vector R(t) = <3/5 cos t, 4/5(1+sin t), cos t>.

3) If V(0) = -2i - 3j and A(0) = 2i + 3j, what is A_T and A_N at t = 0?

4) If V(0) = <5,-2,4> and A(0) = <1,3,-9>, what is A_T and A_N at t = 0?

5) ||V|| = sqrt(e^-t + t^4). What is A_T at t = 0?

6) Where on the trajectory of R(t) = <2t^2 - 5t, 5t + 2, 4t^2> is the speed maximized and minimized?

7) An object moves with a constant angular velocity omega around the circle x^2 + y^2 = r^2 in the xy-plane.

• Find a parameterization for the circle.
• Compute the tangential and normal acceleration for the object.

8) A car which weighs 3,000lbs moves along the elliptic path 1600x^2 + 100y^2 = 1, where x and y are measured in miles. If the car travels at the constant speed of 30mi/hr, how much frictional force is required to keep it from skidding as it turns at (1/40,0)? What about at (0,1/10)?

9) ** Consider the vector function R(t) = <3 sin t, 4t, 3 cos t>.

• Evaluate V(t) = R'(t), N(t), and A(t) = R''(t) when t = 1.
• Find the vector projection of A(1) onto V(1). Denote this proj_V(1) (A(1)).
• Find the vector projection of A(1) onto N(1). Denote this proj_N(1) (A(1)).
• What is the sum of proj_V(1) (A(1)) and proj_N(1) (A(1)).
• How does proj_V(1) (A(1)) relate to A_T when t = 1.
• How does proj_N(1) (A(1)) relate to A_N when t = 1.

10) ** Use the method described in the previous problem to find A_T and A_N for R(t) = <cos t, sin t>.

11) ** Let B = T X N when T and N are the unit tangent and normal vectors to a curve C with position vector R. Show that dB/ds = T X (dN/ds).

12) An object connected to a string of length r is spun counterclockwise in a circular path in a horizontal plane. Let omega be the constant angular velocity of the object.

• Show that the position vector of the object is R(t) = (r cos omega t) i + (r sin omega t) j.
• Find the normal component of the object's acceleration.
• If omega is doubled, what is the effect on the normal component of acceleration?
• What is the effect on A if omega is unchanged but the length of the string is doubled?
• What happens to A if omega is doubled but r is halved?

=====

Section 11.1

`q001.  If f(x, y) = x^2 / 4 - y^2 / 25, then what curve do you get for each of the following?

• f(x, y) = 0?
• f(x, y) = 1?
• f(x, y) = 4?
• f(x, y) = 9?

`q002.  Plot each of the curves obtained in the preceding.

`q003.  If f(x, y, z) = x^2 / 4 + y^2 / 25 - z^2 / 16, then what equation corresponds to the condition f(x, y, z) = 9?  What would the plot of this equation look like in 3-dimensional space?

`q004.  If f(x, y) = x * y then what curve do you get for each of the following?  Sketch each curve.

• f(x, y) = 0?
• f(x, y) = 1?
• f(x, y) = 4?
• f(x, y) = 9?

`q005.  If f(x, y, z) = x * y / z then what equation expresses the condition f(x, y, z) = 36?  What would the plot of this equation look like in 3-dimensional space?

`q006.  Find the x and y partial derivatives of the following functions:

f(x, y) = x^2 sqrt(y)
f(x, y) = cos(x y)
f(x, y) = e^-(x^2 + y^2)
f(x, y) = sqrt(x) * e^y
f(x, y) = cos(x y) + e^(x^2 y)
f(x, y) = x y / (x^2 + y^2)
f(x, y) = sqrt(x^2 / 4 - y^2 / 9)
f(x, y) = y e^(-k x^2) + x y cos(x + y)

1) Let f(x,y,z) = x^2*y*e^(3x) + (x - y + z)^2. Find the following expressions.

• f(0,0,0)
• f(1,-1,1)
• f(-1,1,-1)
• d/dx(f(x,x,x))
• d/dy(f(1,y,1))
• d/dz(f(1,1,z^2))

2) Find the domain and range of the function f(x,y) = x / sqrt(x- y^2).

3) Find the domain and range of the function f(u,v) = sqrt(u cos v).

4) Find the domain and range of the function f(x,y) = e^((x+1)/(y-3)).

5) Sketch and describe the level curves f(x,y) = C for C >= 0 for f(x,y) = y/x.

6) Sketch and describe the level surface f(x,y,z) = 1 when f(x,y,z) = 2x^2 + 2z^2 - y.

7) Sketch and describe the traces of the quadric surface z = x^2/25 - y^2/9.

8) Sketch and describe the graph of the function f(x,y) = y - 3.

9) Sketch and describe the graph of the function f(x,y) = -sqrt(1 - x^2 - y^2).

10) According to the ideal gas law, PV = kT where P is pressure, V is volume, T is temperature, and k is some constant. Suppose a tank contains 3500in^3 of some gas at a pressure of 24lb/in^2 when the temperature is 270K.

• Determine k for this gas.
• Express T as a function of P and V using the k found in the previous step and describe the isotherms.

=====

Section 11.2

1) Find the limit as (x,y) -> (0,0) of (5x^2 - 2xy + 3y^2 -9) or explain why the limit does not exist.

2) Find the limit as (x,y) -> (e,0) of (ln(x^2 + y^2)) or explain why the limit does not exist.

3) Find the limit as (x,y) -> (0,0) of (x^2y^2/(x^2 + y^2)) or explain why the limit does not exist.

4) Find the limit as (x,y) -> (a,a) of ((x^4-y^4)/(x^2 - y^2)) where a is some constant, or explain why the limit does not exist.

5) Find the limit as (x,y) -> (0,0) of (y - x)/sqrt(x^2 + y^2) or explain why the limit does not exist.

6) Find the limit as (x,y) -> (0,0) of [1 - (sin(x^2 + y^2)/(x^2 + y^2)] or explain why the limit does not exist.

7) Explain why the limit as (x,y) -> (0,0) of f(x,y) = (x^2 + y)/(x^2 + y^2) does not exist.

8) Let f(x,y) = (y^2 - x^2)/(x^2 + y^2) for all x and y such that (x,y) isn't (0,0)

• Find the limit as (x,y) -> (2,1) of f(x,y).
• Show that f(x,y) does not have a limit at (0,0).

9) **Let f(x,y) = cos(x^2 + y^2)/(x^2 + y^2) when (x,y) is not (0,0). Using polar coordinates to see for what value of f(0,0) is f(x,y) continuous at (0,0).

10) **Either show that the following statement is true or give a counterexample: If the limit as y -> 0 of f(0,y) is 0, then lim (x,y) -> (0,0) of f(x,y) is also 0.

=====

Section 11.3

Suppose f(x, y) = x^2 * sqrt(y). 

`q001.  What is the function f(x, 4)?

Sketch the graph of this function.

What is the derivative of this function, and what is the value of this derivative when x = 1?

What is the equation of the line tangent to your graph at the x = 1 point?

In terms of the `i, `j and `k vectors, what is a vector in the direction of your tangent line?

`q002.  What is the function f(1, y)?

Sketch the graph of this function.

What is the derivative of this function, and what is the value of this derivative when y = 4?

What is the equation of the line tangent to your graph at the y = 4 point?

In terms of the `i, `j and `k vectors, what is a vector in the direction of your tangent line?

`q003.  Using a single set of coordinate axes, sketch the following:

The point (1, 4, 0)

The point (1, 4, f(1, 4)).

The plane y = 4, and in this plane also sketch the graph of the function f(x, 4).

A vector tangent to your graph at the point (1, 4, f(1, 4)).

In terms of `i, `j and `k, what is the vector you just sketched?

`q004.  Using a single set of coordinate axes, sketch the following:

The point (1, 4, 0)

The point (1, 4, f(1, 4)).

The plane x = 1, and in this plane also sketch the graph of the function f(1, y).

A vector tangent to your graph at the point (1, 4, f(1, 4)).

In terms of `i, `j and `k, what is the vector you just sketched?

`q005.  Sketch the 2 x 2 x 2 cube whose 'bottom' face rests on the x axis, which 'back' face is in the plane x = 1, and whose 'left-side' fact is in the plane y = 4.

Sketch the part of the graph of f(1, y) that lies along the 'back' face of your cube.

Sketch the part of the graph of f(x, 4) that lies along the 'left' face of your cube.

Sketch the vectors tangent to your graph at the point (1, 4, 2).

`q006.  Treating y as a constant, what is the derivative of f(x, y), with respect to x?

For y = 4, what is the value of this derivative?

Have you seen this result before?

For x = 1 and y = 4, what is the value of your derivative?

What does this value have to do with your picture?

`q007.  Treating x as a constant, what is the derivative of f(x, y), with respect to y?

For x = 1, what is the value of this derivative?

Have you seen this result before?

For x = 1 and y = 4, what is the value of your derivative?

What does this value have to do with your picture?

`q008.  You have just calculated the derivatives f_y (x, y) and f_x (x, y).  Specifically

f(x, y) = x^2 * sqrt(y).

f_y (x, y) treats x^2 as a constant.  The derivative with respect to y of sqrt(y) is 1 / (2 sqrt(y)).  So f_y (x, y) = x^2 * 1 / (2 sqrt(y), which simplifies to x^2 / (2 sqrt(y)).

f_x (x, y) treats sqrt(y) as a constant, and yields derivative (2 x) * sqrt(y).

Find f_x (x, y) and f_y ( x, y) for each of the following functions:

• f(x, y) = sqrt(x) y^3
• f(x, y) = e^(2 x) * y^2 + 1 / sqrt(x) * y

`q008.  For the function f(x, y) = x^2 sqrt(y):

Find the x derivative of f_x (x, y).

Find the y derivative of f_y (x, y).

Find the x derivative of f_y (x, y).

Find the y derivative of f_x (x, y).

We call these derivatives, respectively, f_xx, f_yy, f_yx and f_xy.

1) Find f_x, f_y, f_xx, and f_yx when f(x,y) = (x + xy + y)^4. (f_x is the first partial with respect to x, f_yx is the partial with respect to y first and then x)

2) Find f_x and f_y when f(x,y) = xy^4*arctan(y).

3) Find f_x and f_y when f(x,y) = arccos(xy)*e^(x+y).

4) Find f_x, f_y, and f_z when f(x,y,z) = xz*e^y.

5) Find f_x, f_y, and f_z when f(x,y,z) = cos(yz + x).

6) Determine z_x and z_y by differentiating the expression 4x^2 + 2y^2 + 3z^2 = 9 implicitly.

7) Let f(x,y) = (x^2 + y^2)/(xy), P = (2, -1, -5/2)

• Find the slope of the tangent line of the graph of f parallel to the xz-plane at the point P.
• Find the slope of the tangent line of the graph of f parallel to the yz-plane at the point P.

8) Let f(x,y) = x*ln(x+y^2), P = (e, 0 ,e)

• Find the slope of the tangent line of the graph of f parallel to the xz-plane at the point P.
• Find the slope of the tangent line of the graph of f parallel to the yz-plane at the point P.

9)** Determine f_x and f_y for f(x,y) = Int( (e^t + 3t) dt, x^2, 2y). (Remember the second fundamental theorem of calculus.)

10) A function is said to be harmonic on the open set S if f_xx + f_yy = 0 for all (x,y) in S. Show that the following functions are harmonic for the given S.

• f(x,y) = 2ln(x^2 + y^2). S = xy-plane with point (0,0) removed.
• f(x,y) = e^y*cos(x). S = xy-plane.

11) For the two following functions, show that f_xy = f_yx.

• f(x,y) = cos(yx^2).
• f(x,y) = (cos^2(x))*(cos y).

12) In physics the wave equation is given by z_tt = c^2 * z_xx and the heat equation is given by z_t = c^2 * z_xx. In the two following cases, see if z satisfies the wave equation, the heat equation, or neither.

• z = sin(2t)*sin(2 c x).
• z = (e^(-t))(sin (x/c) + cos(x/c).

13) The Cauchy-Riemann equations are u_x = v_y and u_y = -v_x. Do the equations u = e^x*cos y and v = e^x* sin y satisfy the Cauchy-Riemann equations?

14) **Given the central conic p(x,y) = ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0 with ab - h^2 not equal to 0. Show that the center is the intersection of the lines f_x = 0 and f_y = 0.

=====

Section 11.4

`q001.  The surface described by the graph z = f(x, y) = 16 - 4 x^2 + y^2 includes the point (2, 3, 9). 

• If the surface is 'sliced' by the plane x = 2, what is the resulting z vs. y function, and what is its slope at the y = 3 point?
• What is a vector in the x = 2 plane which is tangent to the surface at the given point? 
• If the surface is 'sliced' by the plane y = 3, what is the resulting z vs. x function, and what is its slope at the x = 2 point?
• What is a vector in the x = 2 plane which is tangent to the surface at the given point?
• What is a vector perpendicular to both of the tangent vectors?
• What therefore is the equation of the tangent plane?
• What are the coordinates of the graph point above the point (2.1, 3.2) in the xy plane?
• What are the coordinates of the point on the tangent plane that lies directly above the point (2.1, 3.2) in the xy plane?
• How far is it from the graph to the tangent plane, directly above the point (2.1, 3.2) in the xy plane?
• What do the derivatives f_xx, f_xy and f_yy have to do with how accurately the tangent plane approximates the actual graph in the vicinity of the point (2, 3, 9)?

`q002.  The surface described by the graph z = f(x, y) = 16 - 4 x^2 + y^2 includes the point (2, 1, 1).  Show how to use the derivatives f_x and f_y at this point to find the equation of the tangent plane.  What are the values of f_xx, f_xy and f_yy at this point, and what do they tell you about how the graph 'pulls away' from the tangent plane as you move in various directions.

`q003.  If x is the length and y the width of a rectangle, then

• If the length changes by `dx, by how much does the area change?
• If the width changes by `dy, by how much does the area change?
• If the length changes by `dx and the width by `dy, by how much does the area change?
• If `dx is 3% of x, and `dy is 2% of y, then what fraction of the area change is represented by the product `dx * `dy?
• How accurate is it to therefore say that `d ( x y ) = x * `dy + y * `dx?

`q004.  If z = f(x, y) = x * y, where x and y are both functions of t, then what is the expression for dz / dt?  What therefore is the expression for dz?

`q005.  If w = f(x,y, z) = x^2 * cos(y) * e^z, where x, y and z are all functions of t, then what is the expression for dw/dt?  What therefore is the expression for `dw?

`q006.  It is easy to verify that when x = 3 and y = 4, the value of the function f(x, y) = x^2 * sqrt(y) is 6.  It is also easy to verify that df =  2x sqrt(y) dx + x^2 / (2 sqrt(y)) dy. 

• If x = 3 and y = 4, with dx = .1 and dy = .2, then what is the value of df?
• What therefore would you predict to be the value of f(3.1, 4.2), without actually evaluating the function at (3, 4)?
• Go ahead and evaluate the function at  x = 3.1 and y = 4.2, and compare with your predicted value.
• Use the same type of analysis to predict f(2.2, 8.9), and compare the prediction with the actual value of the function.

1) Give the standard form equation for the tangent plane to the surface z(x,y) = 5 - x^2 -y^2 at the point P_0 = (1,1,3).

2) Give the standard form equation for the tangent plane to the surface z(x,y) = ln(x^2 + y^2) at the point P_0 = (e,0,2).

3) Find the total differential of f(x,y) = 7xy + 3x^2*y + 18x + 9y + 2.

4) Find the total differential of f(x,y,z) = 2xzy^3*cos(xy)*sin(z).

5)** Show that the function f(x,y) = e^(2x + y^2) is differentiable for all (x,y) in R^2.

6) Use an incremental approximation to estimate the function f(x,y) = 2x^3 + 4y^2 at f(1,01, 2.03).

7) Use an incremental approximation to estimate the function f(x,y) = cos(xy) for f(sqrt(pi) + .01, sqrt(pi) - .01).

8) Find the equation of all horizontal tangent planes to the surface z = 4 - x^2 - y^2 + 6x.

9)** Show that if x and y are sufficiently close to zero and f is differentiable at (0,0), then f(x,y) ~= f(0,0) + x*f_x(0,0) + y*f_y(0,0).

• Use the formula in the previous part to show that 1/(1+x-y) ~= 1-x+y for small x and y.
• If x and y are sufficiently close to zero, what is the approximate value of the expression 1/((x+1)^2 + (y+1)^2).

10) It is know that the period T of a simple pendulum with small oscillations is modeled by T = 2*pi*sqrt(L/g) where L is the length of the pendulum and g is the acceleration due to gravity. For a certain pendulum it is known that L = 3.01ft and g = 32.2ft/s^2. What is the approximate error in calculating T by using L = 3ft and g = 32ft/s^2?

11) A football has the shape of an ellipsoid x^2/9 + y^2/36 + z^2/9 = 1 with dimensions in inches. If you know that the leather shell is 1/8in thick, use differentials to estimate the volume of the leather shell. The volume of an ellipsoid with formula x^2/(a^2) + y^2/(b^2) + z^2/(c^2) = 1 is 4/3*pi*abc.

12) Compute the total differentials of x/(x-y) and y/(y-x). Why are these two differentials equal?

=====

Section 11.5

`q001.  If f(x, y) = x^2 sqrt(y), and if x(t) = 2 t^3 while y(t) = t^2, then

• Find the expression for df/dt by using the chain rule df/dt = df/dx * dx/dt + df/dy * dy/dt (note that the 'd' symbols in df/dx and df/dy should be partial-derivative symbols.  The partial derivative symbol is a rounded-off 'd' that looks sort of like a backward '6').
• Evaluate your expression for t = 1.
• Substitute the expressions for x(t) and y(t) into the expression x^2 sqrt(y), to get f as a function of t only. 
• Find the derivative of this function.
• Evaluate your derivative at t = 1.

`q002.  If f(x, y) = x^2 sqrt(y), and if x = u^2 - v^2 while y = u * v, then we know that df = 2 x sqrt(y) dx + x^2 / (2 sqrt(y)) dy.

• What is the expression for dx, in terms of u, v, du and dv?
• What is the expression for dy, in terms of u, v, du and dv?
• Substitute these expressions into df = 2 x sqrt(y) dx + x^2 / (2 sqrt(y)) dy to get an expression for df in terms of x, y, u, v, du and dv.
• Substitute the expressions for x and y directly into the expression x^2 sqrt(y), obtaining an expression in just the variables u and v.
• Find the differential of your expression.
• Show that your differential is the same as the expression you obtained previously for df.

`q003.  Suppose that at a certain clock time t, the quantities x and y take values 2 and 5.  Suppose also that a change of .01 in the value of t causes x to change by .04 and y to change by .07.  Suppose that suppose that the temperature in the immediate neighborhood of the (x, y) point (2, 5) on a thin sheet of metal changes by 60 degrees for every unit of displacement in the x direction, and by 20 degrees for every unit of displacement in the y direction. 

• By how many degrees does x change when t changes by .025?
• By how many degrees does y change when t changes by .025?
• By how many degrees does the temperature change due to the change in x?
• By how many degrees does the temperature change due to the change in y?
• What is the rate of change of x with respect to t?
• What is the rate of change of y with respect to t?
• What is the rate of change of temperature with respect to x?
• What is the rate of change of temperature with respect to y?
• What is the rate of change of temperature with respect to t?
• Write out the symbolic chain-rule expression for dT/dt, where T stands for temperature, in terms of T_x, T_y, dx/dt and dy/dt.  Explain how your expression symbolizes the process by which you answered the preceding questions.

1) Let z = f(x,y) = 2xy + x^2 where x = 3t^2 and y = -4t.

• Find dz/dt after finding z explicitly in terms of t.
• Use the chain rule for one parameter to find dz/dt.

2) Let z = f(x,y) = xy + 1 where x = cos 3t and y = cot 3t.

• Find dz/dt after finding z explicitly in terms of t.
• Use the chain rule for one parameter to find dz/dt.

3) Let F(x,y) = x^2 + y^2 where x(u,v) = u cos(v) and y(u,v) = u + v^2. Let z = F(x(u,v),y(u,v)). Find z_u and z_v in the following ways.

• Expressing z explicitly in terms of u and v.
• Apply the chain rule for two independent parameters.

4) Let F(x,y) = ln(xy) where x(u,v) = e^(uv) and y(u,v) = e^(uv + 1). Let z = F(x(u,v),y(u,v)). Find z_u and z_v in the following ways.

• Expressing z explicitly in terms of u and v.
• Apply the chain rule for two independent parameters.

5) Write out the chain rule for the function w = f(x,y) where x = x(s,t,u,v) and y = y(s,t,u,v).

6) Find dw/dt, where w = xe^(yz^2) and x = cos t, y = sin t, z = tan t.

7) Find w_r where w = e^(x - y + 3z^2) and x = r + t - s, y = 3r - 2t, z = sin(rst).

8) Find dy/dx when  x cos y + y sin x = x.

9) Let x sin z = x + 2y. Find z_xy, z_xx, and z_yy.

10) Let f(x,y) be a differentiable function of x and y and let x = r cos(theta) and y = r sin(theta) for r > 0 and 0 < theta < 2pi.

• If z = f(x(r,theta) , y(r,theta)), find z_r and z_theta.
• **Show that (z_r)^2 + 1/r^2(z_theta)^2 = z_x^2 + z_y^2.

11) The dimensions of a rectangular box are linear functions with respect to time: l(t), w(t), and h(t). The length and width are increasing at 3 in/sec and the height is decreasing at 2 in/sec.

• Find the rate at which the volume V and the surface area S are changing with respect to time.
• If l(0) = 10 ,w(0) = 8, and h(0) = 20, is V increasing or decreasing when t = 5. What about S?

12) The combined resistance of three resistors R is given by the formula 1/R = 1/(R1) + 1/(R2) + 1/(R3). Suppose that at a certain instant R1 = 150 ohm, R2 = 300 ohm, and R3 = 450 ohm. R1 and R3 are decreasing at a rate of 3 ohm/sec and R2 is increasing at a rate of 4 ohm/sec. How fast is R changing at this instant and is it increasing or decreasing?

13) Find z''(theta) where z is a twice differentiable function of theta and z can be written as z = f(cos(theta), sin(theta)). (Hint: What substitution do you make to go from rectangular coordinates to polar coordinates?)

14)** The Cauchy-Riemann equations are u_x = v_y and u_y = -v_x. Show that if x and y are expressed in terms of polar coordinates, the Cauchy-Riemann equations become u_r = 1/r*v_theta and v_r = -1/r*u_theta.

=====

Section 11.6

The upside-down Delta symbol is called 'del', and will by typed accordingly.  This symbol stands for the 'del' operator, which takes the partial derivative with respect to each variable, and multiplies it by the unit vector in the direction of that variable.

Thus for example if we have f(x, y), a function of the 2 variables x and y:

• its x derivative can be denoted f_x, and the unit vector in the x direction is i, giving us f_x i
• its y derivative can be denoted f_y, and the unit vector in the y directionis j, giving us f_y j
• del f is therefore equal to f_x i + f_y j.
• note that since the 'del' operator gives us a vector, it is denoted in boldface type.  We write

del = f_x i + f_y j.

For a function of three or more variables, we must apply a similar process for each variable.  For example if we have the function g(x, y, z) we would get

del g = f_x i + f_y j + f_z k.

The expression del f is called the 'gradient' of f.  The gradient has a number of very useful properties:

• The gradient of a function, evaluated at a given point, gives us a vector in the direction of maximum increase of the function at that point.  Its magnitude is the maximum rate at which the function changes.
• If we take the dot product of the gradient, evaluated at a point, with any unit vector, we get the rate at which the function changes as we move in the direction of that unit vector.
• The equation f(x, y) = c describes a curve in the xy plane.  If (x, y) is a point on that curve, then the gradient, evaluated at that point, is normal to the curve ((i.e., perpendicular to the tangent line at that point).
• The equation f(x, y, z) = c describes a surface in xyz space.  If (x, y, z) is a point on that surface, then the gradient, evaluated at that point, is normal to the surface ((i.e., perpendicular to the tangent plane at that point).

`q001.  Let f(x, y) = x^2 y^3.  Find del f.

`q002.  Let f(x, y, z) = x^2 + x cos y + e^(yz).  Find del f.

`q003.  Find the directional derivative of f(x, y) = x^2 y^3, at the point (2, 1) in the direction of the unit vector u = .6 i + .8 j. 

• If you move .01 unit in the direction of that vector by how much does your directional derivative indicate that the value of f(x, y) will change? 
• What will be your x and y coordinates after the move?
• What is the value of f(x, y) at the point (2, 1)?
• What is the value of f(x, y) at the new point?
• Did the function change by the amount you predicted?

`q004.  The ellipse x^2 / 4 + y^2 / 9 = 1 can be expressed as the curve f(x, y) = 1, with f(x, y) = x^2 / 4 + y^2 / 9.  The point (1, 3 sqrt(3) / 2) lies on the curve.  Find a vector in the direction normal to the curve at that point.

1) Find grad(f) when f(x,y) = ln(x^2 + y). (grad(f) is the gradient of f).

2) Find grad(f) when f(x,y,z) = e^(x+y+z).

3) Find grad(f) when f(x,y,z) = (xz-1)/(y -x).

4) Find the directional derivative of f(x,y) = x^2 + xy at the point (1, -1) in the direction of the vector v = i - j.

5) Find a unit vector which is normal to the surface given by the equation 2 = x^3 + 2xy^2 + 3y - z at the point P = (1,1,1). Also find the equation of the tangent plane at this point using this information.

6) Find a unit vector which is normal to the surface x^2 + y^2 + z^2 = 1 at the point P = (a,b,c). Find the equation of the tangent plane at this point.

7) Find the direction from the point P = (1,e,-1) which the function f(x,y,z) = z ln (y/x) increases the most rapidly and compute the magnitude of the greatest rate of increase.

8) Find the direction from the point P = (a,b) in which the function f(x,y) = ax + by + c increases the most rapidly and compute the magnitude of the greatest rate of increase.

9) Find a unit vector which is normal to the point P = (x0,y0) for the hyperbola x^2/a^2 - y^2/b^2 = 1.

10) Find the directional derivative of f(x,y) = x^2 - 2xy + y^2 at the point P = (1,-1) in the direction toward the origin.

11) Let f have continuous partial derivatives, and assume the maximal directional derivative of f at (0,0) is equal to 100 and attained in the direction of (-4/5, 3/5). Find grad(f) at (0,0).

12)** Let T(x,y) = 1 - x^2 - 2y^2 be the temperature at each point in a metal sheet. A heat-loving bug is placed in the plane at the point P = (-1,1). Find the path that the bug should take to be as warm as possible. Assume at each point on the path, the tangent line will point in the direction at which T increases most rapidly.

13) A particle P1 with mass m1 is located at the origin, and a particle P2 with mass 1 unit is located at the point (x,y,z). According to Newton's law of universal gravitation, the force P1 exerts on P2 is modeled by F = -G(m1(xi + yj + zk))/r^3 where r is the distance between P1 and P2 and G is the gravitational constant.

• Starting from the fact that r^2 = x^2 + y^2 + z^2, show that d/dx*(1/r) = -x/r^3, d/dy*(1/r) = -y/r^3 and d/dz(1/r) = -z/r^3. (Here d/dx denotes partial with respect to x)
• The function V = -G*m1/r is called the potential energy function for the system. Show tha F = -grad(V).

14)** Suppose that u and v are unit vectors and that f has continuous partial derivatives. Show that D_(u+v)(f) = 1/||u+v|| * D_u(f) + D_v(f). (D_u(f) is the directional derivative of f in the direction of u).

=====

Section 11.7

A critical point of a function y = f(x) is a point at which f ' (x) = 0.  If at the critical point  f ''(x) < 0, the derivative is decreasing and the critical point is a maximum; if f ''(x) > 0 the derivative is increasing and the critical point is a maximum.  If f '' (x) = 0, then the test is inconclusive and additional analysis is necessary.

At a point (x0, y0) the function z = f(x, y) yields two functions, z = f(x, y0) and z = f(x0, y).  The first is a function of x and the second is a function of y. 

It is possible that both the x and y functions have a maximum at (x0, y0), in which case we would tend to expect that f(x, y) has a maximum at this point, or that both have minima at (x0, y0),  in which case we would tend to expect that f(x, y) has a minimum.  As we will see, though, it's not quite that simple.

It is also possible that one function has a maximum, while the other has a minimum.  In this case we expect that f(x, y) has a 'saddle point' at (x0, y0).

A saddle point can also occur even if the x and y functions match, in that both have maxima, or both have minima.  This is because the x and y second derivatives indicate the behavior only in the x and y directions.  They don't tell us, for example, what happens if we move in a direction at 45 degrees relative to the x and y directions.  It is entirely possible that, for example, our x and y functions are each have a minimum at a point, with the graph rising if we move from our point in either the x or the y direction, but that the graph falls as we move in a direction at 45 degrees.

The test for max or min of a function of two variables is as follows:

• f_x and f_y are the derivatives in the x and y directions.  If we do have a relative max or a relative min, both f_x and f_y must be zero.  We therefore find the critical points of f(x, y) by solving the equations f_x (x, y) = 0, and f_y (x, y) = 0.
• We then test the second derivatives f_xx and f_yy, which indicate the concavity of our graph in the x and y directions, at each of our critical points.  If the concavity at a critical point is the same in both directions, then it is possible but not certain that our function f(x, y) has a relative max or min at that critical point.
• Note that the concavity is the same in both x and y directions if f_xx and f_yy have the same sign (and neither is zero).  If we multiply two numbers of the same sign, we know that their product is positive.  So the requirement that both have the same sign, with neither being zero, is equivalent to saying that f_xx * f_yy > 0.
• To see whether we do have a max or a min, we also have to test the behavior of the function in the 45-degree direction.  We do this for a critical point by finding the 'mixed partial derivative' f_xy.
• If f_xx * f_yy - f_xy ^2 is still greater than zero, then we can be sure that the 45-degree direction doesn't mess thing up.  In this case we don't have a saddle point, and we have a relative max or relative min, depending on whether f_xx and f_yy are both negative (giving us a relative max) or both positive (giving us a relative min).

`q001.  Let (x0, y0) = (2, 3), and let f(x, y) = 2 x^2 - 7 xy + 4 y^2 - 8.  The given point (x0, y0) is not a critical point for the function, as you will demonstrate:

• What is the function z = f(x, y0)?
• This function f(x, y0) represents the intersection of the graph of f(x, y) with the plane y = y0.  You should sketch its graph.  What is the derivative of this function with respect to x?  What are the critical points of this function?  Does the function f(x, y0) have a max, a min or an inflection point at your critical point(s)?

• What is the function z = f(x0, 0)?
• This function f(x0, y) represents the intersection of the graph of f(x, y) with the plane x = x0.  You should sketch its graph.  What is the derivative of this function with respect to y?  What are the critical points of this function?  Does the function f(x0, y) have a max, a min or an inflection point at your critical point(s)?

• Do the critical points of f(x, y0) coincide with the critical points of f(x0, y)?  Do you therefore conclude that (x0, y0) is or is not a critical point of the function f(x, y)?

`q002.  Find f_x and f_y for the function f(x, y) = 2 x^2 - 7 xy + 4 y^2 - 8.  Set both of your expressions equal to zero.  This will give you two simultaneous equations in x and y. 

• Solve the two equations to find the critical point(s).

Find f_xx, f_yy and f_xy.

At each of your critical points, determine whether f_xx is positive or negative (or zero), and determine the same for f_yy.  Let each critical point in turn be (x0, y0).

• Do your results indicate that the x function f(x, y0) has a max or a min?  If so, which is it?
• Do your results indicate that the y function f(x0, y) has a max or a min?  If so, which is it?

At each of your critical points find the value of f_xy, the value of f_xx * f_yy and the value of f_xx * f_yy - f_xy ^2.

• Using your values conclude whether the function has a max, a min or a saddle point at the critical point.

1) Consider f(x,y) = 3x^2 - 5xy + y^2 + 3. Find the critical points, and classify each point as either a relative maximum, relative minimum, or saddle point.

2) Consider f(x,y) = e^(-y) cos(x). Find the critical points, and classify each point as either a relative maximum, relative minimum, or saddle point.

3) Consider f(x,y) = e^(-(x^2 + y^2)). Find the critical points, and classify each point as either a relative maximum, relative minimum, or saddle point.

4) Consider f(x,y) = x^2 - y^2 + xy/16. Find the critical points, and classify each point as either a relative maximum, relative minimum, or saddle point.

5) Consider f(x,y) = x^2 +  2xy + y^2. Find the absolute extrema on the closed bounded set S = {(x,y) | x^2 + y^2 <= 1}.

6) Consider f(x,y) = x^3 - 2xy + y^2 + 3x. Find the absolute extreme on the closed bounded set S = {(x,y) | 0 <= x,y <= 2}.

7) Find the least squares regression line for the set of points {(4,-2), (3,-1), (0,0), (-1,3), (-2,1), (-3,2)}.

8) Find three positive numbers whose sum is 38 and whose product is as large as possible.

9) A particle of mass m in a rectangular box with dimensions x,y,z has ground state energy E(x,y,z) = k^2/(8m) * (1/x^2 + 1/y^2 + 1/z^2) where k is a physical constant. Find the values of x,y,z that minimize the ground state energy in the following cases.

• If the volume of the box is 30 and x = y.
• If the volume of the box is 45.
• If the volume of the box is V.

10)** We can use the exponential and logarithm to help us to linearize data that does not tend to change linearly. The following problems will demonstrate this.

• Suppose we have y = kx^m. Show that by taking the natural logarithm of this equation we obtain a linear relationship Y = K + mX. Explain these new variables and the constant K.
• The data that follows relates the periods of revolution, t (in days), of the six inner planets and to their semimajor axes a (in 10^6 km). Kepler conjectured that the relationship is t = ka^m for some k and m. Transform the data as in the first part and find k and m.

t-data : (87.97, 224.7, 365.26, 686.98, 4332.59, 10759.2) 

a-data : (58, 108, 149, 228, 778, 1426).

11) Consider these following functions, at each of which D = 0 at a critical point. Show whether each of the following is true or false:

• f(x,y) = x^4 - y^4 has a saddle point at (0,0).
• g(x,y) = x^2*y^2 as a relative minimum at (0,0).
• h(x,y) = x^3 + y^3 as a relative maximum at (0,0).

12)** Consider the function f(x,y) = (x - y^2)(x - 2y^2). Discuss the behavior of this function at (0,0).

13)** Prove the second partials test. As a start compute the second directional derivative of f in the direction of the unit vector u = hi + kj and complete the square.

=====

Section 11.8

1) Maximize the function f(x,y) = x^2 + y^2 subject to the constraint x + y = 12.

2) Maximize the function f(x,y) = e^(xy) subject to the constraint x^2 + y^2 = 1.

3) Maximize the function f(x,y,z) = xyz subject to the constraint x + 2y + 3z = 12.

4) Maximize the function f(x,y,z) = x^2 + y^2 + z^2 subject to the constaint x^2 + 2y^2 + 4z^2 = 4.

5) Find the minimum and maximum values of f(x,y,z) = x + 2y - z on the sphere x^2 + y^2 + z^2 = 100.

6) Find the minimum and maximum distance from the origin to the ellipse 5x^2 -6xy + 5y^2 = 4.

7) Post office regulations specify that a box can be mailed parcel post only if the sum of its length and girth (if dimensions are x,y,z, girth is 2x + 2y and z is length) does not exceed 108 in. Find the maximum volume of such a package.

8)** Heron's formula says that the area of a triangle with sides length a,b,c is given by sqrt(s(s-a)(s-b)(s-c)) where s = 1/2*(a+b+c). Show that given a fixed parameter P, the equilateral triangle has the largest area.

9) Find the maximum of f(x,y,z) = xyz subject to the constraints x^2 + y^2 = 3 and y = 2x.

10)** A farmer wants to build a metal silo in the shape of a right circular cylinder with a right circular cone on top. The bottom of the silo will be a concrete slab. What is the least amount of metal that can be use if the silo is to have a fixed volume V0.

11) Use Lagrange multipliers to optimize f(x,y) = 2x + 2y subject to the constrain xy = 1/4. In this case you will recieve two candidates for an extremum. Explain.

12) Show that the cost function C(x,y) = px + qy is minimized subject to the fixed construction level Ax^(alpha)*y^(beta) = k with alpha + beta = 1 when x = k/A(alpha*q/(beta*p)^(beta), y = k/A(beta*p/(alpha*q))^(alpha).

=====

Section 12.1

`q001.  Evaluate the integral of x^2 y^3 with respect to y, treating x as a constant, between the limits y = -1 and y = 2.

Then integrate the resulting expression from x = 0 to x = 2.

`q002.  In the preceding integral we integrated with respect to y over the interval from y = -1 to y = 2, then we integrated the result with respect to x over the interval from x = -1 to x = 1.

If at every point of the x interval [-1, 1] we sketch a line segment from y = -1 to y = 2, we 'fill in' a region of the xy plane.  Sketch this region.  Describe the region you have sketched.

`q003.  Evaluate the integral of x^2 y^3 with respect to x, between the limits x = -1 and x = 1.  Then integrate the resulting expression with respect to y, from y = -1 to y = 2.  Compare with your solution to the first problem.

If at every point of the y interval [-1, 2] we sketch the line segment from x = -1 to x = 1, we fill in a region of the xy plane.  Sketch and describe this region. 

Explain how the description of the region you have sketched here compares with the description of the region you sketched in the preceding problem.

`q004.  Evaluate the integral of x^2 y^3 with respect to y, treating x as a constant, between the limits y = 0 and y = x.

Then integrate the resulting expression from x = 0 to x = 2.

`q005.  In the preceding integral we integrated with respect to y over the interval from y = 0 to y = x, then we integrated the result with respect to x over the interval from x = -1 to x = 1.

If at every point of the x interval [-1, 1] we sketch a line segment from y = 0 to y = x, we 'fill in' a region of the xy plane.  Sketch this region.  Describe the region you have sketched.

`q006.  Now integrate x^2 y^3 with respect to y from y = 0 to y = sqrt(x), and integrate the resulting expression from x = 0 to x = 4. 

Then sketch the corresponding region, where x varies from 0 to 4 and for every x the value of y varies from 0 to x^2.

Describe your region.

`q007.  Over what x interval does the line y = 1 intersect the region you sketched in the preceding?

Over what interval does the line y = 1/2 intersect the same region?

Over what interval does the line y = 3/2 intersect the region?

Over what interval does the line y = c intersect the region?

What is the maximum value of c for which the line y = c has a nonempty intersection with the region?  What is the minimum such value of c?

Call these values y_0 and y_f.  What are the valuees of y_0 and y_f?

What is the significance of the interval [y_0, y_f] of the y axis?

`q008.  We could describe the region as follows:

At every point of the y interval [0, 2], we sketch the line segment from x = __ to x = 4.

What expression should we use to fill in the blank?

`q009.  Integrate x^2 y^3 with respect to x, from x = y^2 to x = 4.  Then integrate the result with respect to y from y = 0 to y = 2.

Sketch the region of integration, and explain in detail how you constructed your sketch

`q010.  Consider the region 0 <= x <= 4, x^2 <= y <= 2.

If we partition the x interval from 0 to 4 into a number of small subintervals, then what part of our region corresponds to the typical subinterval, whose length we denote by `dx and which contains a sample point x_hat?

`q011.  Continuing the preceding, if we partition y interval of the 'strip' corresponding to our previous x subinterval (the 'strip' runs from x = 0 to about y = sqrt( x_hat )) into small subintervals, what will be the shape and dimensions of the typical subinterval whose length is `dy and which contains the sample point y_hat?  What will be its area?

`q012.  Continuing the preceding, if the density at the point (x, y) of the region is x^2 y^3, then what is the mass corresponding to the region of dimensions `dx by `dy, provided we regard the density at the point (x_hat, y_hat) to be the average density of that region?

... limit as 'small' approaches 'infinitesimal'

Find the area of the region you described in ... .

... partition ...

... interpret as mass, find centroid, center of mass, moment of inertia, etc.

1) Evaluate the iterated integral

Int( Int(( x^2 + 2xy + y^2 ) dy,0,2) dx, 0, 1)

Explanation of notatation:  The notation Int(( x^2 + 2xy + y^2 )dy,0,2) means 'the integral of x^2 + 2 x y + y^2 with respect to y, between the limits y = 0 and y = 2'.  That integral would be written in standard form as

The notation

Int( Int(( x^2 + 2xy + y^2 ) dy,0,2) dx, 0, 1)

contains the above integral on the 'inside', then the integral of this result evaluated with respect to x from x = 0 to x = 1.  The resulting double integral looks like this:

2) Evaluate the iterated integral Int ( Int( 1/(x+y)^3 dy, -1, 2) dx), 2,3).

The inner integral, followed by the complete integral, are written as follows:

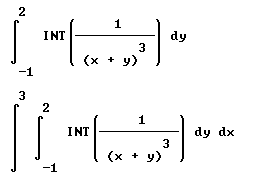
3) Evaluate the double integral over R with respect to A of 7  where R: 2 <= x <= 4, 1 <= y <= 5.

4) Evaluate the double integral over R with respect to A of x/4  where R: 1 <= x <= 8, -2 <= y <= 0.

5) Compute the double integral over R with respect to A of (1 + x^2)/(4 + y^2)  where R: 0<= x <= 1, 0 <= y <= 1.

6) Compute the double integral over R with respect to A of cos(x+y)  where R: 0 <= x <= pi/2, 0 <= y <= pi/2.

7) Find the volume of the solid bounded above by the graph of z = f(x,y) and below by the xy-plane when f(x,y) = ye^(xy) and R: 0 <= x <= ln2, 0 <= y <= 1.

8) Let R be a rectangular region within the boundary of a certain city defined by R: -2 <= x <= 3, -1 <= y <= 1. The units are in miles and (0,0) is the city center. Assume the population density is 13*e^(-0.08)r thousand people per square mile and r = sqrt(x^2 + y^2). Give the double integral which will model the total population of this region.  Do not, however, solve the integral.

9) Compute the double integral over R with respect to A of ln(sqrt(x))/xy  when R is the rectangle 1 <= x <= e, 1 <= y <= 4.

10) Use a grid with 16 cells to approximate the volume under the surface of 4 - x^2 - y^2, above the rectangle R: 0 <= x <=1, 0 <= y <= 1.

11) **Let f be a function with continuous second partial derivatives over a rectangular region R with vertices (x1,y1), (x1,y2), (x2,y1) and (x2,y2) where x1 < x2 and y1 < y2. Show that the double integral over R with respect to A of f_xy is equal to f(x1,y1) - f(x2,y1) + f(x2,y2) - f(x1,y2) using the Fundamental Theorem of Calculus.

12) **Let f(x,y) = (y-x)/(x + y)^3 and define R: 0 <= x,y <= 1. Find the double integral of f(x,y) over R with respect to A using both orders of differentiation. Why is it that the two integrals have different answers and why do they not violate Fubini's theorem.

=====

Section 12.2

1) Evaluate the double integral Int( Int( dy, x^2, 4x)) dx, 0, 4]).

2) Evaluate the double integral Int( Int((2x + 3y) dy), -1, x) dx, -1, 1).

3) Evaluate the double integral Int( Int((x^2* e^xy) dy), 0, x) dx, 0 , 1).

4) Evaluate the double integral Int( Int(sqrt(1 + sin^2(x)) * sin x arccos y dx), 0, pi/2) dy, 0, 1).

 5) Integrate 4x over D with respect to A using a double integral where D is the region bounded by 4 - x^2, y = 3x, and x = 0.

6) Integrate 1/(y^2 + 1) over D with respect to A using a double integral where D is the triangle bounded by x = 2y, y = -x, and y = 2.

7) Compute the following integral with the given order of integration and with the order changed: Int[ Int(4x^3 dy, 0, sqrt(x)) dx, 0, 4].

8) Give an equivalent integral with the order of integration reversed. Int[ Int( f(x,y) dy, arctan x, pi/4) dx, 0, 1]

9)** Set up a double integral for the solid remianing when a square hole with side 3 is drilled through a sphere with radius 2.

10) Give two different ways to set up the integral of the area of the region D where D is the region in the first quadrant of the xy-plane bounded by y = 6/x^2 and y = 5 - x^2. Evaluate one of these integrals.

11) Reverse the order of integration in Int[ Int( f(x,y) dy, x, x^3) dx, 1,2] + Int[ Int(f(x,y) dy, x, 8) dx, 1,2].

12)** Let f(x,y) be continuous on a region D and m <= f(x,y) <= M for all (x,y) in D.

• Show that mA <= Double integral over D of f(x,y) with respect to A <= MA, where A is the area of D.
• Use the previous step to estimate the value of the double integral of e^(x cos y) over D with respect to A where D is the triangle with vertices (0,-1),(0,2),(1,0).

=====

Section 12.3

1) Evaluate the double integral Int( Int(sqrt(1-r^2)*r dr), 1,2) dtheta, 0, pi/2). Sketch and describe the region of integration.

In standard notation:

2) Evaluate the double integral Int( Int(dr, 0, 1 + sin(theta)) dθ), 0 , pi). Sketch and describe the region of integration.

In standard notation the integral looks like this:

3) Use a double integral to find the area of the region described by 0 <= r <= 3 cos(5theta).

4) Use a double integral to find the area of the region described by 1 <= r <= 3 sin(θ).

5) Use a double integral to find the area bounded by the parabola r = 5/(1 + cosθ) and the lines θ = 0, θ = π/3 and r = 5/2* secθ.

6) Use polar coordinates to find the double integral of f(x,y) = x^2 + y^2 over D with respect to A where D is the circular disk defined by x^2 + y^2 <= a^2 for some a > 0.

7) Use polar coordinates to find the double integral of f(x,y) = ln( a^2 + x^2 + y^2) over D with respect to A where D is the circular disk defined by x^2 + y^2 <= a^2 for some a > 0.

8) Use polar coordinates to find the double integral of f(x,y) = sqrt(x^2 + y^2) over D with respect to A where D is the region inside the circle x^2 + (y-1)^2 = 1 in the fourth quadrant.

9) Use polar coordinates to find the double integral of f(x,y) = 1/ sqrt(9 - x^2 - y^2) over D with respect to A where D is the region inside the circle x^2 + y^2 = 4 in the first quadrant.

10) Find the volume of the solid bounded above by the sphere x^2 + y^2 + z^2 = 20 and below by the parabola z = x^2 + y^2.

11) Use polar coordinates to find to integrate x^2 + y^2 over the region D which the upper part of a "washer"-shaped region (annulus) with inner radius 1 and outer radius 4.

12) **Let I = Int(e^(-x^2) dx, -inf, inf). Show that I = sqrt(pi). Note that Int(e^(-x^2) dx, -inf, inf) * Int(e^(-y^2) dy, -inf, inf) = Int[ Int(e^-(x^2 + y^2) dx, -inf, inf) dy, -inf, inf].

=====

Section 12.4

1) Find the surface area of the portion of the plane 4x + y + x = 9 that lies in the first octant.

2) Find the surface area of the portion of the surface z = y^2 that lies over the triangular region in the plane with vertices (0,0,0), (1,0,0) and (0,1,0).

3) Find the surface area of the portion of the sphere x^2 + y^2 + z^2 = 36 that lies above the plane z = 4.

4) Find the surface area of the portion of the parabola z = 9 - x^2 - y^2 that lies above the xy-plane.

5) Find the surface area of the portion of the cylinder x^2 + y^2 = 16 that lies within the cylinder x^2 + z^2 = 16 .

6) Find a formula for the surface area of the frustrum of the cone z = 9sqrt(x^2 + y^2) between the planes z = h1 and z = h2 where h1 > h2.

7) Find the surface area of the portion of the cylinder x^2 + z^2 = 9 which lies above the triangle with vertices (0,0,0), (1,1,0), (1,0,0).

8) Set up (but do no solve) the double integral for the surface area of the surface given by e^(-x)*cos y over the disk  x^2 + y^2 <= r^2

9) Compute the magnitude of the fundamental cross product for the surface parametrically described by R(u,v) =(2u sin v)i + (2u cos v)j + (u^2 sin2v)k.

10) Consider the surface S which is a sphere of radius a.

• Find a parameterization for S.
• Using this parameterization find the fundamental cross product and its magnitude.
• Find the surface area for S, does it match up with the familiar formula for surface area of a sphere?

11) Find the surface area of the torus which is parametrically described as R(u,v) = (a + b cos v)cos u i + (a + b cos v)sin u j + vk. Where 0 < b < a, 0 <= u,v <= 2pi.

12)** Let S be the surface defined by f(x,y,z) = C, and let R be the projection of S onto a plane. Show that the surface area of S can be computed by the double integral of (||grad(f)||/(|grad(f) dot u|) with respect to A where u is a unit vector normal to the plane containing R and grad(f) dot u is non-zero.

=====

Section 12.5

1) Compute the iterated triple integral Int( Int( Int(dx,4,5) dy,-2,1) dz,1,3)

2) Compute the iterated triple integral Int( Int( Int(x^2*y sin(xyz) dz, 0,1) dy,0,1) dx,0, pi)

3) Evaluate the triple integral of xz + 2yx over D with respect to V where D is the box 2<= x <= 4, 1 <= y <= 3, -1 <= z <= 1.

4) Evaluate the triple integral of  x^2*y over D with respect to V where D is the tetrahedron with vertices (0,0,0), (3,0,0), (0,2,0), (0,0,1).

5) Evaluate the triple integral of xy over D with respect to V where D is the solid in the first octant bound by the hemisphere sqrt(4-x^2 - y^2) and the coordinate planes.

6) Use a triple integral to find the volume of the solid bounded by y = 4 - x^2, z = 0, and z = y.

7) Use a triple integral to find the volume of the solid bounded by x^2 + y^2 + z^3 = 8 and z = 1.

8) Use a triple integral to find the volume of the solid bounded by the cylinders y = z^2 and y = 2 - z^2 and the planes x = 1 and x = -2.

9) Change the order of integration of the triple integral Int(Int(Int(f(x,y,z) dz, 0, 1-2x) dy, 0, 1-4x^2) dx, 0, 1/2) to dy dx dz.

10) Find the volume of the region between the two elliptic paraboloids z = x^2/4 + y^2 - 9 and z = -x^2/4 - y^2 + 9.

11) Use triple integration to find the volume of the following solids.

• A sphere of radius r.
• An ellipsoid with equation x^2/a^2 + y^2/b^2 + z^2/c^2 = 1 (a,b,c > 0).

12)** Do the folowing steps to help to solve the integral I = Int[Int[Int(sin((pi - z)^3) dz) dy] dx] over V where D is the region bounded below by the xy-plane, above by the plane x = z, and laterally by the planes x = y and y = pi.

• Change the order of integration to show that Int[Int (f(u) du,0,v) dv, 0, x] = Int( (x-u)*f(u) du, 0, x).
• Change the order of integration to show that Int[Int[Int(f(w) dw, 0, u) du, 0, v] dv, 0, x] = 1/2*Int( (x-w)^2*f(w) dw, 0, x).
• Use the two above steps to evalutate I.

13) Evaluate the 4-tuple (quadruple) integral of e^(x +2y - z - w) with respect to w, z, y, x in that order over H. H is the four-dimensional region bounded by the hyperplane x + y + z + w = 4 and the coordinate spaces x =0, y = 0, z = 0 and w = 0 where x,y,z,w >= 0.

=====

Section 12.6

1) Find the centroid for a lamina with delta = 4 over the region bounded by the curve y = sqrt(x) and the line x = 9 in the first quadrant.

2) Find the center of mass of the part of the spherical solid with density delta = 2 described by x^2 + y^2 + z^2 <= 9, x,y,z >= 0.

3) Use double integration to find the center of mass when delta(x,y) = k*(x^2 + y^2) over the region x^2 + y^2 <= a^2, y >= 0.

4) Use double integration to find the center of mass when delta(x,y) = y over the region y = e^-x, x = 0, x = 3, y = 0.

5) Find I_x, the moment of inertia about the x-axis, of the lamina that covers the region bounded by the graph of y = 3 - x^2 and the x-axis, and with density delta(x,y) = x^2*y^2.

6) Find the center of mass of the cardioid r =1 + sin(theta) if the density at each point (r,theta) is delta(r,theta) = r.

7) Show that a homogenous lamina of mass m that covers the circular region x^2 + y^2 = a^2 will have moment of inertia ma^2/4 with respect to both the x- and y-axes. What is the moment of inertia with respect to the z-axis?

8) Find the center of mass of the tetrahedrom in the first octant bounded by the plane x/a + y/b + z/c where a,b,c > 0. Assume delta = x.

9) Suppose the joint probability density function for the random variables X and Y is f(x,y) = {4e^(-2x)*e^(-y) if x,y >= 0, 0 otherwise.} Find the probability that X + Y <= 1.

10) Suppose X measures the time (in minutes) that a person stands in line at a certain bank and Y, the duration (in minutes) of a routine transaction at the teller's window. You arrive at the bank to deposit a check. If the joint probability function for X and Y is modeled by f(x,y) = { 1/16*e^(-x/4)*e^(-y/2) if x,y >= 0, 0 otherwise} Find the probability that you complete your business at the bank within 10 minutes.

11) Find the average value of the function f(x,y,z) = x + 2y + 3z over the solid region S bounded by the tetrahedron with vertices (0,0,0), (1,0,0), (0,1,0), (0,0,1).

12) The radius of gyration for revolving a region R ,with mass m, about an axis of rotation ,with moment of inertia I, is d = sqrt(I/m). Find the radius of gyration about the x-axis of the semicircular region x^2 + y^2 <= a, y >= 0 given that the density at (x,y) is directly proportional to the distance of the point from the x-axis.

13) A solid has the shape of a rectangular parallelepiped given by -a <= x <= a, -b <= y <= b, -c <= z <= c and its density is delta(x,y,z) = x^2 * y^2 * z^2.

• Guess the location of the center of mass and the value of the moment of inertia about the z-axis.
• Check your guess by direct computation.

14)** Prove the following area theorem of Pappus: Let C be a curve of length L in the plane. The the surface obtained by rotating C about the axis L in the plane has area 2pi*Lh, where h is the distance from the centroid of C to the axis of rotation.

=====

Section 12.7

1) Convert the point (sqrt(2), 2, -sqrt(3)) from rectangular coordinates to both cylindrical and spherical coordinates.

2) Convert the point (-3, 2pi/3, 3) from cylindrical coordinates to both rectangular and spherical coordinates.

3) Convert the point (pi,pi,pi) from spherical coordinates to both rectangular and cylindrical coordinates.

4) Convert the equation z = x^2 + y^2 to cylindrical coordinates.

5) Convert the equation 3x^2 + 3y^2 + 3z^2 = 1 to spherical coordinates.

6) Convert the equation rho = sin(theta)*cos(phi) to rectangular coordinates.

7) Evaluate the iterated integral Int( Int( Int(rho^2*sin(phi) d(rho), 0, cos(phi)) d(theta),0, pi/4) d(phi), 0, pi/2).

8) Evaluate the iterated integral Int( Int( Int( r dz, 0, 4cos(theta)) dr, 0, sin(theta)) d(theta), 0, pi/2).

9) Use cylindrical coordinates to compute the triple integral of z(x^2 + y^2)^(-1/2) with respect to V over D where D is the solid bounded by the plane z = 2 and below by the surface 4z = x^2 + y^2.

10) Evaluate the triple integral of sqrt(x^2 + y^2 + z^2) with respect to V over R where R is the region defined by x^2 + y^2 + z^2 <= 5.

11) Find the volume of the region D where D is the region defined by the paraboloid z = 1 - 9(x^2 + y^2) and the xy-plane.

12) Find the volume of the region D where D is the region defined as the intersection of the solid sphere x^2 + y^2 + z^2 <= 16 and the solid cylinder x^2 + y^2 <= 4.

13) Let D be a homogenous solid (with density delta) that has the shape of a right circular cylinder with height and radius r. Use cylindrical coordinates to find the moment of inertia of S about its axis of symmetry.

=====

Section 12.8

1) Find the Jacobian d(x,y)/d(u,v) (For this section, d denotes the partial symbol) when x = 2u - v and y = 4u - 3v.

2) Find the Jacobian d(x,y,z)/d(u,v,w)  when x = 2u - v, y = 2v + 2w, z = v - w.

3) Find the Jacobian d(x,y)/d(u,v)  when u = 3x + y and v = -x + y.

4) Find the Jacobian d(x,y)/d(u,v) when u = x/(x^2 + y^2) and v = y/(x^2 + y^2).

5) Let R be the parallelogram with vertices (0,0), (1,4), (4,6), (4,2). Sketch and decribe the corresponding region after the transformation u = x^2, v = x+ y.

6) Suppose the uv-plane is mapped onto the xy-plane by the equations x = 2uv, y = u^2 - v^2. Express dx dy in terms of du dv.

7) The region R bounded by the parabolas y = x^2, y = 4x^2, y = sqrt(x), and y = 1/2sqrt(x).

8) Let D be the region in the xy-plane which is bounded by the coordinate axes and the line x + y = 1. Use the change of variables u = x + y and v = x - y to compute the double integral of (x-y)*e^(x^2 + y^2) over D with respect to A

9) Under the transformation u = 1/5(2x + y) and v = 1/5(x - 2y) the region D which is a square in the xy-plane with vertices (0,0), (1,-2) is mapped onto a square in the uv-plane. Use this information to find the integral of cos(2x + y)*sin(x - 2y) with respect to V over D.

10) Under the change of variables x = s^2 - t^2, y = 2st, the quarter circular in the st-plane given by s^2 + t^2 <= 1, s >= 0, t >= 0 is mapped onto a certain region D* of the xy-plane. Find the integral of 1/(sqrt(x^2 + y^2) over D* with respect to V.

11)** Use a change of variables to find the moment of inertia about the z-axis of the solid ellipsoid with density 1 and equation x^2/a^2 + y^2/b^2 + z^2/c^2 = 1.

12) A rotation of the xy-plane through the fixed angle theta is given by x = u cos(theta) - v sin(theta), y = u sin(theta) + v cos(theta).

• Compute the Jacobian of this transformation.
• Let E denote the ellipse x^2 + xy + y^2 = 9. Use a rotation of pi/4 to obtain an integral which is equivalent to the double integral of y with respect to V over E.
• Evaluate the integral found in the previous step.

13) Find the Jacobian of the cylindrical coordinate transformation x = r cos(theta), y = r sin(theta), z = z.

14)** Let T: x = x(u,v), y = y(u,v) be a one-to-one transformation on a set D so that T^-1 has the form u = u(x,y), v = (x,y). Use the multiplicative property of determinants along with the chain rule, to show that d(x,y)/d(u,v) * d(u,v)/d(x,y) = 1. You may assume that all needed partial derivatives exist.

=====

Section 13.1

The del operation can be notated as d_x i + d_y j, where d_x means 'take the partial derivative with respect to x' and d_y means 'take the partial derivative with respect to y'.  Thus for example d_x f means 'take the partial derivative with respect to x of f', so that using f_x for the derivative with respect to x we have d_x f = f_x.

The del operator has already been seen in connection with the gradient.

The del operator is used to define gradient, divergence, and curl.  Chapter 13 explores the implications of these definitions.  In Section 13.1 we simply learn to perform the operations, and learn a few basic properties.

If f is a scalar function then del f = (d_x i + d_y j ) f = d_x f i + d_y f j =  f_x i + f_y j..  This is the gradient of f.

If F(x, y) = F_1(x, y) i + F_2(x, y) j, then the divergence of the function F is del dot F = (d_x i + d_y j ) dot (F_1 i + F_2 j ) = d_x F_1 + d_y F_2 = F_1_x + F_2_y.

The divergence and gradient can be defined for functions of 2 variables.

The 'curl' can be defined only for a function of 3 variables. 

If F(x, y) = F_1(x, y) i + F_2(x, y) j + F_3(x, y) k then the curl of F is

curl F = del X F = (d_x i + d_y j + d_z k) X (F_1 i + F_2 j + F_3 k) = (F_3_y - F_2_z) i - (F_3_x - F_1_z) j + (F_2_x - F_1_y) k

(this is easier to see in determinant notation).

* 1) Find div F and curl F when F(x,y) = x y i + (x^2 + y^2)j.

* 2) Find div F and curl F when F(x,y) = (sin x)i + (cos x)j + k at the point P = (pi, pi/4, 0).

* 3) Find div F and curl F when F(x,y) = (e^y cos x)i + (e^y sin x)j + k at the point P = (3,-1,-2).

* 4) Find div F and curl F when F = xi - yj.

* 5) Find div F and curl F when F = axi + byj + czk, where a,b,c are real numbers.

* 6) Find div F and curl F when F = (xi + yj + zk)/sqrt(x^2 + y^2 + z^2).

7) Is the function r(x,y,z) = xyz harmonic?

* 8) Find div F, given that F = grad(f), where f(x,y,z) = x^2*y^3*z.

9) If F(x,y,z) = i + 3xj + 2yk and G(x,y,z) = 2xi - 3yk +5 zk, then find div(F X G).

10) If F(x,y) = u(x,y)i + v(x,y)j, show that curl F = 0 if and only if du/dy = dv/dx (Here d denotes the partial symbol).

11) Which (if any) of the following is the same as div(F X G) for all vector fields F and G.

•  (div F)(div G)
• (curl F) dot G - F dot (curl G)
• F(div G) + (div F)G
• (curl F) dot G + F dot (curl G)

12) Prove that the curl of the gradient of a function is always 0.

13) Let R = <x,y,z> and r = ||R|| = sqrt(x^2 + y^2 + z^2). If curl R = 0 then what is div R?

14)** Let F = <x^2y, yz^2, zy^2>. Either find a vector field G such that F = curl G, or show that no such G exists.

=====

If x(t) and y(t) are smooth continuous functions, then the parametric equations x = x(t), y = y(t) define a curve in the x-y plane.  We can call this curve C.  Between clock times t = t1 and t = t2, the distance we travel along the curve C is given by the line integral

integral ( sqrt( x ' (t)^2 + y ' (t)^2) dt, as shown in more detail below:

If t is interpreted as time, then the vector x ' (t) i + y ' (t) j is interpreted as the velocity vector v(t).  If we multiply the velocity vector by a short time interval `dt, we get the approximate displacement vector `ds = v(t) `dt.  Summarizing the situation at clock time t:

• At clock time t, we are at the point (x(t), y(t)) of the curve C, our velocity at that instant is v(t) and our displacement between t and t + `dt is approximately equal to `ds = v(t) `dt.= (x ' (t) i + y ' (t) j) * `dt

Our actual points on the curve C are (x(t), y(t)) and (x(t + `dt), y(t + `dt)).

• If we move from point (x(t), y(t)) to point (x(t + `dt), y(t + `dt)) then our vector displacement between these two instants is very close to x ' (t) `dt i + y ' (t) `dt j, and we therefore move a distance very close to sqrt( (x ' (t) `dt)^2 + (y ' (t) `dt)^2)
• We can simplify this expression to sqrt (x ' (t))^2 + ( y ' (t) )^2 ) `dt, abbreviated simply sqrt( x ' ^2 + y ' ^2) `dt.

If we want to know how far we move during a longer interval between t = t1 and t = t2, during which our speed and/or our direction might change significantly, we begin by partitioning the t interval into shorter intervals. 

The typical subinterval is characterized by duration `dt_i and sample point t_hat_i. 

Evaluating x ' and y ' at our sample point, our approximate displacement during the interval is x ' (t_hat_i) `dt_i i + y ' (t_hat_i) `dt_i `j and our distance is sqrt( x ' ^ 2 + y ' ^2) `dt_i, where is is understood that x ' and y ' are evaluated at t = t_hat_i.

If we sum our distances over all subintervals and take the limit as interval size shrinks to 0, we get the integral int( sqrt( x ' ^2 + y ' ^2) dt ), which is called a line integral.  This particular line integral simply evaluates the distance we travel along our path.

`q001.  Sketch and describe the path defined by x(t) = cos(t) and y(t) = 2 sin(t), 0 <= t <= pi/2.

This path is our curve C.  Find, but do not evaluate, the integral for the distance traveled along this path. 

Solution:  The integral is integral( x ' (t)^2 + y ' (t)^2 ) dt, t from 0 to pi/2. 

x ' (t) = sin(t) and y ' (t) = 2 cos(t), so the integral becomes

integral ( sqrt(sin^2(t) + 4 cos^2(t) ) dt, t from 0 to pi / 2.

Suppose now that our curve C represents the shape of a thin object (think of a wire) whose density is given by some function f(x, y), in the sense that the average density is multiplied by the length to get the mass.

Again considering the i_th subinterval of our partition:

The length of the subinterval is again sqrt( x ' ^2 + y ' ^2 ) `dt_i, where x ' and y ' are evaluted at the sample point t_hat_i.

The approximate average density on the subinterval will be taken to be f(x(t_hat_i), y(t_hat_i)).

So the mass of the subinterval is approximate

`dm_i = f(x, y) sqrt(x ' ^ 2 + y ' ^2) `dt_i, where again x, y, x ' and y ' are evaluted at sample point t_hat_i.

Summing up our masses and taking the limit as partition mesh approaches zero, we find that the total mass is

integral ( f(x, y) sqrt( x ' ^2 + y ' ^2) dt, t from 0 to pi/2).

Effectively we have simply inserted the density function f(x, y) into the arc length integral.

`q002.  If the curve in the first question represents a curved wire whose density at point (x, y) is f(x, y) =  4 + x^2 + y^2, then what is the total mass of the wire?

Solution:  Our arc length increment is represented by sqrt( x ' ^2 + y ' ^2 ) dt, our density by our function f(x, y), so our mass increment is density * length

• dm = f(x, y) sqrt(x ' ^2 + y ' ^ 2 ) dt.

Our total mass is therefore

integral ( f(x, y) sqrt( x ' ^2 + y ' ^2 ) dt, t from 0 to pi / 2)

= integral ( (4 + x^2 + y^2) sqrt( x ' ^2 + y ' ^2 ) dt, t from 0 to pi / 2)

= integral ( (4 + cos^2(t) + 4 sin^2(t) ) sqrt( sin^2(t) + 4 cos^2(t) ), t from 0 to pi / 2).

Now suppose we want to find the work done by a force field F ( x, y ) = F_1(x, y) i + F_2(x, y) j as we move along this path. 

• On our typical subinterval our displacement is x ' (t_hat_i) `dt_i i + y ' (t_hat_i) `dt_i `j and the force is F_1(x, y) i + F_2(x, y) j , where F_1 and F_2 are evaluated at x(t_hat_i), y(t_hat_i)). 
• The work on this interval is the dot product of the force and the displacement:

  `dW_i = F dot `ds_i

  = F(x, y) dot ( x ' (t_hat_i) `dt_i i + y ' (t_hat_i) `dt_i `j )  

  = ( F_1(x, y) i + F_2(x, y) j ) dot (x ' i + y ' j ) `dt_i

  = (F_1 * x ' + F_2 * y ') `dt_i.

  Again all quantities are evaluted at the sample point t_hat_i in our i_th time subinterval, so in detail the above quantity is

  (F_1 (x_hat_i, y_hat_j) * x ' (x_hat_i, y_hat_j)  + F_2 (x_hat_i, y_hat_j) * y ' (x_hat_i, y_hat_j) ) `dt_i

  It's easier to look at the expression

  (F_1 * x ' + F_2 * y ') `dt_i,

  but the preceding line indicates exactly what this expression means

   

• When we sum the contributions over the various subintervals and take limits we obtain an integral which we can evaluate.  Specifically the integral is

  integral ( F_1 * x ' + F_2 * y ' ) dt, t from t1 to t2.

`q003.  Find, but don't evaluate, the integral for the work done by the force function F(x, y) = x^2 y i + x y^2 j over the path C of question `q001.

Solution: 

The path is defined by x(t) = cos(t) and y(t) = 2 sin(t), 0 <= t <= pi/2.

The force function on this path, at clock time t, is therefore

F (x(t), y(t) ) = x(t)^2 y(t) i + x(t) y(t)^2 j = cos^2(t) * 2 sin(t) i + cos(t) * (2 sin(t) )^2 j = 2 cos^2(t) sin(t) i + 4 cos(t) sin^2(t) j

and our displacement increment is

ds = v (t) dt =  (x ' (t) i + y ' (t) j ) dt = (-sin(t) i + 2 cos(t) j ) dt,

so our integral is

integral ( F dot `ds )

= integral ( ( 2 cos^2(t) sin(t) i + 4 cos(t) sin^2(t) j ) dot ((-sin(t) i + 2 cos(t) j ) dt), t from 0 to pi/2)

= integral ( ( -2 cos^2(t) sin^2(t) + 8 cos^2(t) sin^2(t) ) dt, t from 0 to pi/2)

= integral ( (6 cos^2(t) sin^2(t)) dt, t from 0 to pi / 2).

Section 13.2

* 1) Evaluate Int[ (2x - 3y) ds, C] where C is defined by x = sin t, y = cos t, 0 <= t <= pi. ( Int[ f(x,y) ds, C] is the line integral of f(x,y) over C).

* 2) Evaluate Int[-y dx + 3y dy, C] where C is defined by y^2 = x from the point (1,1) to the point (9,3).

* 3) Evaluate Int[ (y-x) dx + (x^2*y) dy, C] where C is the quarter-circle x^2 + y^2 = 4 from (0,2) to (2,0).

4) Consider Int[(y^2 - x^2) dx - x dy, C]. Evaluate this integral for the following curves C:

• C is the arc of the parabola y = x^2 from (0,0) to (2,4).
• C is the segment of the line y = 2x for 0 <= x <= 2.

* 5) Evaluate Int[(x^2 - y^2)dx + x dy, C] where C is the circular path given by x = 2 cos(theta), y = 2sin(theta), 0 <= theta <= 2pi.

6) Evaluate Int[ F dot dR, C] where F = (5x + y)i + x j and C is the vertical line from (0,0) to (0,2) followed by the horizontal line from (0,2) to (2,2)

* 7) Consider Int[ -y dx + x dy + xz dz, C]. Evaluate this integral for the following curves C:

• C is the helix defined by x = cos t, y = sin t, z = t for 0 <= t <= 2pi.
• C is the unit circle x^2 + y^2 = 1, z = 0, traversed once counterclockwise as viewed from above.

* 8) Evaluate Int[F dot dR, C], where F = (y - 2z) i + xj - 2xyk and C is the path given by R(t) = ti + t^2j - k for 1 <= t <= 2.

9) Evaluate Int[ye^(xz) ds, C], where C is the line segment from (0,0,0) to (2,1,3).

10) Evaluate Int[F dot T ds] where F = -3yi + 3xj + 3xk and C is the straight line segment from (0,0,1) to (1,1,1).

11) Evaluate Int[ (x^2 + xy + y^2)/z^2 ds, C], where C is the path given by R(t) = (cos t)i + (sin t)j - k.

12) Evaluate Int[ (dx + dy)/(|x| + |y|), C] where C is the square |x| + |y| = 1, traversed once clockwise.

13) A force acting on a point mass located at (x,y) is given by F = yi + 2xj. Find the work done by this force as the point mass moves along a straight line from (1,0) to (0,1).

14)** Find the center of mass of a wire in the shape of the helix x = 3 sin t,  y = 3 cos t, z = 2t for 0 <= t <= pi and the density delta(x,y,z) as follows:

• delta(x,y,z) = z
• delta(x,y,z) = x

=====

Section 13.3

If our F function is the divergence del f of some function f(x, y), our work integral over a path C will be just a function of the initial point (x(t1), y(t1)) and the final point (x(t2), y(t2)).  We call f a potential function and our line integral is the potential difference of the function f between the points. 

It is easy to prove that the curl of a conservative field is 0.  Since a conservative field F is the gradient of a potential function f, we need only prove that del X del f = 0.  Using determinant notation and the fact that del f = f_x i + f_y j + f_z k, this is only a matter of writing out the determinant, evaluating it and showing that the result is zero.

It takes a little more work to prove that if the curl of a vector field F is always zero, then the field is the gradient of some function f, and is therefore conservative.

`q001.  Find F ( x, y ) =  del f, if f(x, y) = x^3 y^2 - x sqrt(y).  Then find del X F(x, y).

Solution: 

del f = (x^3 y^2)_x i - (x sqrt(y) )_y j = 3 x^2 y^2 i - x / (2 sqrt(y)) j. 

If we know that the field F( x, y ) = F_1(x, y) i + F_2(x, y) j is conservative then the potential function f(x, y) has the following characteristics:

• F_1(x, y) = f_x (x, y)
• F_2(x, y) = f_y (x, y).

Thus if we integrate f_x (x, y) = F_1 (x, y) with respect to x (treating y as constant) we should get our function f(x, y).  The integration constant can be a function of y, since y is treated as a constant.

If we integrate f_y (x, y) = F_2 (x, y) with respect to y (treating x as constant) we should also get our function f(x, y).  This integration also has an integration constant which, since x is treated as constant, can be a function of x.

`q002.  If F(x, y) = F_1(x, y) i + F_2(x, y) j =  (3 x^2 y^2 - sqrt(y)) i + (2 x^3 y - x / (2 sqrt(y) + 2 y) j, then

• What is the general integral of F_1(x, y) with respect to x? 
• What is the general integral of F_2(x, y) with respect to y?
• Is it possible to reconcile the two general integrals?

Solution:

Integrating F_1 ( x, y) = 3 x^2 y^2 - sqrt(y) with respect to x, we treat y as a constant. 

Our general antiderivative is x^3 y^2 - x sqrt(y) + c, where c is an integration constant.

Since y is treated as a constant, c can be any function of y only.  So we can write our general antiderivative as

f(x, y) = x^3 y^2 - x sqrt(y) + g(y),

where g(y) is any function of y.

Integrating F_2 (x, y) = 2 x^3 y - x / (2 sqrt(y)) + 2 y with respect to y, we treat x as a constant.

Our general antiderivative is x^3 y^2 - x sqrt(y) + y^2 + c, where c is an integration constant.

Since x is treated as a constant, c can be any function of x only.  So we can write our general antiderivative as

f(x, y) = x^3 y^2 - x sqrt(y) + y^2 + h(x),

where h(x) is any function of x.

Thus we have

• f(x, y) = x^3 y^2 - x sqrt(y) + g(y)

and also

• f(x, y) = x^3 y^2 - x sqrt(y) + y^2 + h(x).

These two expressions for f(x, y) appear to be different, but they do agree on the first two terms x^3 y^2 - x sqrt(y).

If the remaining expressions g(y) from the first and y^2 + h(x) in the second can be reconciled, then the two expressions can be the same.

Thus if we can find functions g(y) and h(x) with the property that

g(y) = y^2 + h(x),

we will have a solution.  In fact this works out easily, if we just let g(y) = y^2 and h(x) = 0.  Our first expression for the function becomes

• f(x, y) = x^3 y^2 - x sqrt(y) + g(y) = x^3 y^2 - x sqrt(y) + y^2

and our second becomes

• f(x, y) = x^3 y^2 - x sqrt(y) + y^2 + h(x) = x^3 y^2 - x sqrt(y) + y^2

It is easy to verify that for this function, del (f(x, y) ) is equal to our function F ( x, y ).

Our function x^3 y^2 - x sqrt(y) + y^2 is called a scalar potential for F ( x, y ).

It is worth noting that adding a constant number k doesn't affect this result.  The function x^3 y^2 - x sqrt(y) + y^2 + k, where k is a constant number, is also a scalar potential for our function.

If a vector field F(x, y) has a scalar potential f(x, y), then if A = (x1, y1) and B = (x2, y2) are any two points of the x-y plane, then the integral F (x, y) dot `ds is path-independent for all paths connecting A and B, in the following sense:

If C is any path starting at A and ending at B, then the integral of F (x, y) dot `ds over the path is equal to f(x2, y2) - f(x1, y1).

It follows that if C1 and C2 are both paths both starting at A and ending at B, the integral of F (x, y) dot `ds over the path C2 is equal to integral of F (x, y) dot `ds over the path C1.

`q003.  For the function F(x, y) =  (3 x^2 y^2 - sqrt(y)) i + (2 x^3 y - x / (2 sqrt(y) + 2 y) j of the preceding problem, find the line integral of F dot `ds for the straight line connecting the points (0, 0) and (2, 1), and also the line integral of F dot ds for the path defined by x = 2 t, y = t^2, 0 <= t <= 1.

Solution:

The 'cheap' solution is as follows:

• The second path connects the t = 0 point (2 * 0, 0^2) = (0, 0) to the point (2 * 1, 1^2) = (2, 1).
• So does the first path.

The scalar potential f(x, y) corresponding to the given function F (x, y) was found in the preceding problem to be f(x, y) = x^3 y^2 - x sqrt(y) + y^2.

The integral along any path connecting (0, 0) and (2, 1) is therefore

• integral = f(2, 1) - f(0, 0) = 2^3 * 1^2 - 2 sqrt(1) + 1^2 = 8 - 2 + 1 = 7.

We can detail the solution for either path:

For the second path, dx/dt = 2 and  dy/dt = 2 t, so dx = 2 dt and dy = 2 t dt so `ds = ( 2 i + 2 t j ) `dt.

It is straightforward to calculate F dot `ds and verify that the integral does indeed come out to be 7.

For the first path we can use the parameterization x = 2 t, y = t and obtain the same result.

* 1) Determine if the vector field F= (xe^(xy) sin y) i + (e^(xy)cos xy + y) j is conservative, and if it is then find a scalar potential.

* 2) Determine if the vector field F = (y- x^2)i + (2x + y^2)j is conservative, and if it is find a scalar potential

* 3) Consider the integral Int[ 2x^2y dx + x^3 dy, C]. Evaluate it on each of the following curves C:

• The semicircle x = sqrt(1-y) from -1 <= y <= 1.
• The line segment from (0,-1) to (1,1) and then the line segment from (1,1) to (0,1).
• The square with vertices (1,1), (-1,1), (-1,-1), (1,-1) traversed once clockwise.

* 4) Show that F = e^-yi - xe^-yj is conservative and find a scalar potential f for F. Evaluate the line integral  Int[ F dot dR, C], where C is any smooth path connecting (0,0) and (1,1).

5) Show that the vector field F = (y sin z)i + (x sin z + 2y)j + (xy cos z)k is a conservative vector field and find the scalar potential f for F.

6) Show that the vector field F= <3x^2*y^2*z, 2x^3*yz, x^3*y^2 - e^-z> is conservative and evaluate Int[ F dot dR, C], where C is any smooth path connecting (1,0,-1) to (0,-1,1).

7) Show that the vector field F = <2xz^3 - e^(-xy)y sin z, -xe^(-xy) sin z, 3x^2*z^2 + e^(-xy)cos z> is conservative and evaluate Int[ F fot dR, C], where C is any smooth path connecting (1,0,-1) to (0,-1,1).

* 8) Verify that the integral Int[(xy cos (xy) + sin (xy))dx + (x^2 cos(xy)) dy, C] is independent of path and evaluate it where C is any path from (0, pi/18) to (1, pi/6).

9) Evaluate the line integral Int[ (xy^2 i + x^2yj) dot dR, C] Where C is any path from (4,1) to (0,0).

10)** Find a function g so that g(x)F(x,y) is conservative where F(x,y) = (x^2 + y^2 + x)i + xyj.

11) Consider the line integral I = Int[(-y/x^2 + 1/x)dx + (1/x)dy, C].

• ** Over what region in the xy-plane will the line integral I be independent of path?
• Evaluate the line integral I if C is defined by R(t) = (cos^3(t))i + (sin 3t)j for 0 <= t <= pi/3.

12) Let F(x,y) = (-yi + xj)/(x^2 + y^2).

• Compute Int[F dot dR, C1] where C1 is the upper semicircle y = sqrt(1-x^2) traversed counterclockwise.
• Compute Int[F dot dR, C2] where C2 is the lower semicircle y = -sqrt(1-x^2) traversed counterclockwise.
• **Show that if F = Mi + Nj then d/dy(-y/(x^2 + y^2)) = d/dx(x/(x^2 + y^2)) but that F is not conservative on the unit circle x^2 + y^2 = 1. (d denotes the partial symbol here)

13) Show that if the vector field F(x,y,z) = M(x,y,z)i + N(x,y,z)j + P(x,y,z)k is conservative then dP/dy = dN/dz, dM/dz = dP/dz, dN/dx = dM/dy. (here d denotes the partial derivative)

14) Let f and g be differentiable functions of one variable. Show that the vector field F = [f(x) + y]i + [g(y) + x]j is conservative and find the corresponding potential function.

=====

Section 13.4

In the context of a function F(x, y) = F_1 (x, y) i + F_2 (x, y) j we find that the line integral of F dot `ds around a rectangle with sides of length `dx and `dy parallel to the coordinate axes, in the vicinity of the point (x, y), is close to the value of the area integral of (-F_1_y + F_2_x), taken over the entire rectangle.

In the notation of the text, F_1(x, y) is the function M(x, y) and F_2 (x, y) is the function N(x, y), so that F(x, y) = M i + N j.  The line integral of F dot `ds around a closed curve C is just the integral

integral( M dx + N dy, integrated around the curve C).

If the functions M and N are reasonably well-behaved and the curve C isn't too pathological, then the result for the original small rectangle can be extended to the entire curve and the integral is equal to the area integral (which will be expressed as a double integral):

integral ( (N_x - M_y) dA, integrated over the region inside the curve).

This is a fairly remarkable result, indicating that the behavior of a vector function inside a region can be predicted by its behavior just on the boundary of the region (and vice versa).  This result and its extensions (Stokes' Theorem and the Divergence Theorem) are of wide applicability in the theory of electromagnetism, thermal energy flows and hydrodynamics, to mention only a few of the many applications.

`q001.  Identify the functions M and N in the following: 

integral( 3 x^2 y dx + 5 x e^sqrt(x^2 + y^2) dy, integrated along the arc of a circle of radius 1 centered at the origin).

integral( sqrt( x y) dy - x y / (x^2 + y^2) dx, integrated around boundary of the rectangle 1 <= x <= 3, 1 <= y <= 2)

Solution:

M is the coefficient of dx, N the coefficient of dy. 

So for the first integral, M(x, y) = 3 x^2 y  and N(x, y) = 5 x e^sqrt(x^2 + y^2)

For the second integral, N(x, y) =  sqrt( x y) and M(x, y) = - x y / (x^2 + y^2).

`q002.  What is the integrand for the area integral corresponding to each of the integrals in the preceding?  Those integrals are

integral( 3 x^2 y dx + 5 x e^sqrt(x^2 + y^2) dy, integrated along the arc of a circle of radius 1 centered at the origin).

and

integral( sqrt( x y) dy - x y / (x^2 + y^2) dx, integrated around boundary of the rectangle 1 <= x <= 3, 1 <= y <= 2).

Solution:

The area integral has integrand N_x - M_y . 

For the first integral , M(x, y) = 3 x^2 y and N(x, y) = 5 x e^sqrt(x^2 + y^2).  So M_y = 3 x^2, and N_x = 5 e^sqrt(x^2 + y^2) + 10 x y e^sqrt(x^2 + y^2).

The integrand is therefore 3 x^2 - (5 e^sqrt(x^2 + y^2) + 10 x y e^sqrt(x^2 + y^2)).

For the second integral, N(x, y) =  sqrt( x y) and M(x, y) = - x y / (x^2 + y^2).  The integrand is N_x  - M_y  = y / (2 sqrt( x y ) ) - ( -x / (x^2 + y^2) + 2 x y^2 / (x^2 + y^2)^2).

`q003.  Parameterize the curves and set up the integrals given in the first question.

The integrals are

integral( 3 x^2 y dx + 5 x e^sqrt(x^2 + y^2) dy, integrated along the arc of a circle of radius 1 centered at the origin).

integral( sqrt( x y) dy - x y / (x^2 + y^2) dx, integrated around boundary of the rectangle 1 <= x <= 3, 1 <= y <= 2)

Solution: 

The circle of the first integral can be parameterized by x(t) = cos(t), y(t) = sin(t), 0 <= t M= 2 pi.  Note that this parameterization takes use in the positive (i.e., counterclockwise) direction around the circle.  With this parameterization out integral is

integral ( 3 cos^2(t) sin(t) * (-sin(t) dt) + 5 cos(t) e^sqrt(cos^2(t) + sin^2(t)) * cos(t) dt, t from 0 to 2 pi)

= integral ( -3 cos^2(t) sin^2(t) + 5 cos^2(t), t from 0 to 2 pi).

This integral is perfectly feasible using standard methods.

The rectangle of the second integral can be parameterized on each of its four sides. 

The first side runs from x = 1 to x = 3, with y = 1, so that dy = 0, yielding integral(  -x * 1 / (x^2 + 1^2) dx, x from 1 to 3) .  The integrand simplifies to -x / (1 + x^2).

The second side runs from y = 1 to y = 2, with x = 3, so that dx = 0, yielding integral (sqrt(3 y) dy, y from 2 to 3).

The third side runs from x = 3 to x = 1 with y = 2 and dy = 0, yielding integral( -2 x / (x^2 + 4) dx, x from 3 to 1).

The fourth side yields integral ( sqrt(y) dy, y from 2 to 1).

All these integrals are straightforward (the first and third use substitution u = 1 + x^2 and u = 4 + x^2, respectively).

`q004.  Set up the area integrals corresponding to the line integrals of the preceding.

Solution:

As we found in the second question, the integrand for the first area integral is 3 x^2 - (5 e^sqrt(x^2 + y^2) + 10 x y e^sqrt(x^2 + y^2)).

The region is the circle of radius 1 centered at the origin, which can be described by -1 <= x <= 1, -sqrt(1 - x^2) <= y <= sqrt(1 - x^2).

Our integral is therefore

int( int( 3 x^2 - (5 e^sqrt(x^2 + y^2) + 10 x y e^sqrt(x^2 + y^2)) dy, -sqrt(1-x^2), sqrt(1 - x^2)), dx, -1, 1).

The exponential of the first part cannot be integrated in closed form.  Our only hope for evaluating this integral is to do the line integral we found in the preceding solution.  Fortunately, if the present integral is important, this appears to be straightforward.

The integrand corresponding to our second line integral is y / (2 sqrt( x y ) ) + x / (x^2 + y^2) - 2 x y^2 / (x^2 + y^2)^2.  The region is straightforward, and our area integral is

int(int(y / (2 sqrt( x y ) ) + x / (x^2 + y^2) - 2 x y^2 / (x^2 + y^2)^2) dx, 1, 3) dy, 1, 2).

The integration is possible using methods of first-year calculus, and the result should agree with the line integral of the preceding question.  Doesn't look like it does, but it should.  If it doesn't, then see if you can find the error(s) in these solutions.

* 1) Use Green's Theorem to evaluate Int[ y^3 dx - x^3 dy, C] where C is parameterized by x = cos(theta), y = sin(theta) and 0 <= theta <= 2pi. Check your answer by computing the line integral without Green's Theorem.

* 2) Use Green's Theorem to evaluate Int[4y dx - 3x dy, C] where C is the ellipse 2x^2 + y^2 = 4. Parameterize C to find the value of the integral without using Green's Theorem to check your answer.

3) Use Green's Theorem to evaluate Int[ e^x dx - sin x dy, C] where C is the square with vertices (0,0), (1,0), (1,1), (0,1) traversed counterclockwise.

4) Use Green's Theorem to evaluate the integral Int[ (x + y)dx - (3x - 2y)dy, C] where C is the trapezoid with vertices (0,0), (0,4), (2,4), (3,0) traversed clockwise.

* 5) Use Green's Theorem to evaluate the integral Int[2x arctan(y) dx - x^2*y^2.(1 + y^2) dy, C] where C is the square with vertices (0,0), (3,0), (3,3), (0,3) traversed clockwise.

* 6) Find the work done when an object moves in the force field F(x,y) - 2y^2i + 3x^2j counterclockwise around the circular path x^2 + y^2 = 4.

* 7) Using a line integral, find the area enclosed in the triangle with vertices (0,0), (1,2), (0,3). Check your answer using a geometric formula.

8) Using a line integral, find the area enclosed in the semicircle y = sqrt(9 - x^2). Check your answer using a geometric formula.

9) Evaluate the integral Int[ -2y dx + 3x dy, C] where C is the cardioid r = 1 + sin(theta) traversed counterclockwise.

10)** Using a line integral and polar transformation formulas, show that the area formula in polar coordinates is A = 1/2 Int[ r^2 d(theta), (theta1), (theta2)] = 1/2 Int[(g(theta))^2 d(theta), (theta1), (theta2)].

11) Evaluate Int[ (x dx + y dy)/(x^2 + y^2), C] where C is any smooth Jordan curve...

• ... not enclosing the origin traversed counterclockwise.
• ...enclosing the origin traversed counterclockwise.

12) Evaluate Int[ dz/dn ds, C] where z(x,y) = 2x^2 + 3y^2, and C is the circular path x^2 + y^2 = 16 traversed counterclockwise. (Here d denotes the partial symbol).

13) Evaluate Int[ x*dx/dn ds, C] where C is the bounday of the unit square 0 <= x,y <= 1 traversed counterclockwise. (Here d denotes the partial symbol)

14)** Suppose f is a harmonic function over D and D is a simply connected region enclosed by the Jordan curve C, show that the double integral of (f_x^2 + f_y^2) over D is equal to Int[ f*df/dn ds, C]. (Here d denotes the partial symbol.)

=====

Section 13.5

To evaluate integral ( f(x, y)  ) dS, where S is the surface lying above a region of the xy plane, we simply integrate sqrt( 1 + f_x^2 + f_y^2) over the plane region. 

You should understand why, based on your understanding of the 'multiplier' sqrt( 1 + f ' ^2) for an arc length integral of a function f(x) of one variable, and in terms of a normal vector at a point of the surface z = f(x, y) as the cross product of the vectors i + f_x k and j + f_y k.  However, whether you fully understand this or not, the formula will work for basic problems.

* 1) Evaluate the surface integral Int[Int[2xy dS, S]] where S is the surface described by z = 10, and x^2 / 4 + y^2 <= 1.

* 2) Evaluate the surface integral Int[Int[(x^2 + y^2) dS, S]] where S is the surface described by z = 4 - x, 0 <= x,y <= 2.

* 3) Write out but do not evaluate the surface integral Int[Int[(x^2 + y^2) dS, S]] where S is the surface described by z = xy, x^2 + y^2 <= 4, x > 0, y >= 0.

4) Let S be the hemisphere x^2 + y^2 + z^2 = 4 with z >= 0. Evaluate Int[Int[(z^2) dS,S]].

* 5) Let S be the hemisphere x^2 + y^2 + z^2 = 4 with z >= 0. Evaluate Int[Int[(x^2 + y^2) dS,S]].

6) Let S be the portion of the paraboloid z = x^2 + y^2 where z <= 4. Evaluate Int[Int[1/sqrt(1 + 4z) dS, S]].

* 7) Evaluate Int[Int[ F dot N dS, S]], where F = xi + 2yj + zk, S is the surface of the cube bounded by the planes x = 0, x = 1, y = 0, y = 1, z = 0, z = 1. N is the outward directed normal field.

8) Evaluate Int[Int[ F dot N dS, S]], where F = 2xi - 3yj, and S is the part of the hemisphere given by x^2 + y^2 + z^2 = 5 for z >= 1., N is the outward directed normal field.

* 9) Evaluate Int[Int[ (3x - y + 2z) dS,S]], where S is given by the parameterization R(u,v) = ui + uj - vk, 0 <= u <= 1, 1 <= v <= 2.

10) Evaluate Int[Int[ (arctan x + y - z^2) dS, S]] where S is given by the parameterization R(u,v) = ui + v^2j - vk.

11) Evaluate Int[Int[F dot N dS, S]], where F = xi + yj + z^4k and S is the parametric surface x = u cos v, y = u sin v, z =u for 0<= u <= 2, 0 <= v <= 2pi.

* 12) Find the mass of the homogenous lamina that has the shape of S where S is the surface z = 1 - x^2 - y^2, with z >= 0 and delta = x^2 + y^2 + z^2.

13)** Show that the moment of inertia of a conical shell about its axis is 1/2ma^2 where m is the mas and a is the radius of the cone. Assume delta(x,y,z) = 1.

===== =====

Section 13.6

* 1) Verify Stokes' theorem given F = 2xyi + z^2k, and the surface S being the portion of the paraboloid y = x^2 + z^2 with y <= 4.

* 2) Use Stokes' theorem to evaluate the line integral Int[x^3y^2 dx + dy + z^2 dz,C] where C is the circle x^2 + y^2 = 1 in the plane z = 1 traversed counterclockwise when viewed from the top.

3) Use Stokes' theorem to evaluate the line integral Int[y dx - 2x dy + z dz, C] where C is the intersection of the surface z = x^2 + y^2 and the plane x + y + z = 1 considered counterclockwise when viewed from above the origin.

* 4) Use Stokes' theorem to evaluate the line integral Int[y dx + z dy + y dz, C] where C is the intersection of the sphere x^2 + y^2 + z^2 = 4 and the plane x + y + z = 0, traversed counterclockwise when viewed from above the origin.

* 5) Evaluate Int[ F dot dR, C] where F = <x - z, y - x, z - y> and C is the boundary of the triangular region with vertices (12,0,0), (0,3,0), (0,0,12) traversed counterclockwise as viewed from above.

* 6) Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS,S]] where F = yi + zj + xk and S is the part of the plane x + y + z = 1 that lies in the first octant.

* 7) Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS,S]] where F = <x arctan(e^-x), y ln(1 + y^(3/2)), ze^(-1/z)> and S is the part of the sphere x ^2 + y^2 + z^2 = 9 that lies inside of the cone z = sqrt(2x^2 + 2y^2).

8) Use Stokes' theorem to evaluate the line integral Int[ (1 + y)z dx + (1 + z)x dy + (1 + x)y dz, C] for any closed path C in the plane 2x - 3y + z = 1.

9) The vector field V represents the velocity of a fluid flow, find the circulation Int[V dot dR, C] assuming a counterclockwise orientation when viewed from above where V = yi + ln(x^2 + y^2)j + (x + y)k, and C is the triangle with vertices (0,0,0), (1,0,0), (0,1,0).

10)** Let F = zi + xj + yk and suppose S is a smooth surface in R^3 whose boundary is given by x = 2 cos(theta), y = 3 sin(theta) and z = sin(theta) where 0 <= theta <= 2pi. Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS, S]].

11)** Faraday's law of electromagnetism says that if E is the electric intensity vector in a system, then Int[ E dot dR, C] = -d(phi)/dt (Here d denotes the partial symbol) around any closed curve C, where t is time and phi is the total magnetic flux directed outward through any surface S bounded by C. Given that phi = Int[Int[B dot N dS,S]] where B is the magnetic flux density show that curl E = -dB/dt. Note that it can be shown that d/dt*Int[Int[B dot N dS,S]] = Int[Int[dB/dt dot N dS,S].

12)**Suppose f and g are functions of x,y,z with continuous first- and second-order partial derivatives and C is a closed curve bounding the surface S. Use Stokes' Theorem to verify that Int[ f*grad(g) dot dR, C] = Int[Int[ grad(f) X grad(g)) dot N dS, S]].

===== =====

Section 13.7

* 1) Verify the divergence theorem for F = xzi + y^2j + 2zk where D is the ball x^2 + y^2 + z^2 <= 4. Assume N is the unit normal vector field pointing away from the origin.

* 2) Use the divergence theorem to evaluate the surface integral Int[Int[ F dot  N dS, S]] where F = xyzj, S is the cylinder x^2 + y^2 = 9 for 0 <= z <= 5 and N is the outward unit normal vector field.

3) Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS,S]] where F = 2yi - zj + 3xk, S is the surface comprised of the five faces of the unit cube 0 <= x,y,z <= 1 where z = 0 is missing and N is the outward unit normal vector field.

* 4) Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS,S]] where F = curl(yi + xj - zk), S is the hemisphere z = sqrt(4 - x^2 - y^2) together with the disk x^2 + y^2 <= 4 in the xy-plane and N is the outward unit normal vector field.

5) Use Stokes' theorem to evaluate Int[Int[ curl F dot N dS,S]] where F= xy^2i + yz^2j + x^2zk; S is the surface bounded above by the sphere rho = 2 and below by the cone phi = pi/4 (in spherical coordinates) and N is the outward unit normal vector field.

6) Suppose that S is a solid surface which encloses a solid region D. Let N be an outward unit normal vector to S

• **Show that the volume of D is given by V(D) = 1/3 Int[Int[(xi + yj + zk) dot N dS, S]].
•  Use the formula to find the volume of the hemisphere z = sqrt(R^2 - x^2 - y^2).

* 7) The moment of inertia about the z-axis of a solid D of constant density delta = a is given by Iz = Int[Int[Int a(x^2 + y^2) dV, T]]]. Express this integral as a surface integral over the surface S that bounds D.

8) Show that if g is harmonic in the region D, then Int[ Int[ dg/dn dS, S]] = 0 where the closed surface S is the boundary of D. (Here d denotes the partial symbol).

* 9) An electric change q located at the origin produces the electric field E = qR/(4*pi*epsilon*||R||^3). Where R = xi + yj + zk and epsilon is a physical constant called the electric permittivity.

• Show that Int[Int[E dot N dS, S]] = 0 if the closed surface does not enclose the origin. This is called Gauss's law.
• Show that Int[Int[E dot N dS, S]] = q/epsilon when the surface does enclose the origin, note that the divergence theorem does not apply directly to this case.

=====

=====

173-related sequence of questions:

dy/dx = x^2 * y gives the rate at which y changes with respect to x at the point (x, y).

Plot the point (4, 2) and label its coordinates.

What is the rate at which y changes with respect to x when x = 4 and y = 2?  (just plug in)

If x then changes by .2 units, by how many units does y change?

At what point do you therefore end up?

Plot this point and label its coordinates.

Plug this back into the same equation dy/dx = x^2 * y to find the rate at which the function changes at the new point.

If x changes by another .2 units, by how many units does y change?

At what point do you therefore end up?

Plot this point at label its coordinates.

Plug this back into the same equation dy/dx = x^2 * y to find the rate at which the function changes at the new point.

Continue the process for two more steps.

From precalculus you should remember than b ^ x = e^(x ln(b) ).  Apply the chain rule to find the derivative of this function.

What therefore is the equation of the tangent line to T(t) = .87 * 1.14 ^ t, at t = 5?  It's completely legitimate, of course, to use your calculator to evaluate 1.14 ^ 5.

What therefore is the differential approximation to T (5.001), based on your value of T(5)?

Find the derivative of sin ( 1 / x).  Show the details, write down the appropriate rule(s), and apply them carefully.

Find the derivative of (1.5 x + 7) / (2 x^2 + 3.25).  Show the details, write down the appropriate rule(s), and apply them carefully.

With your calculator in radian mode, as it must be for any calculation involving derivatives and integrals of trig functions, evaluate 4 sin^2 ( .3 x ) / x for six equally spaced points between x = 1.2 and x = 3.3 (the six points include these two points).  Give the six points and your corresponding values below:

Into how many subintervals do your six x values divide the given interval?

Sketch the trapezoidal approximation to this graph and find the slope on each subinterval.  Give your results below, and explain one of your calculations in detail:

Find the area of each trapezoid.  Give your results below, and explain one of your calculations in detail:

Now find the areas of the rectangles formed, and the total of these areas, if you use the left-hand endpoint of each interval as the 'altitude'.  Give your results below, and explain one of your calculations in detail:

Find the areas of the rectangles formed, and the total of these areas, if you use the right-hand endpoint of each interval as the 'altitude'.  Give your results below, and explain one of your calculations in detail:

What is the difference between your left- and right-hand approximations?

What is the difference between the x = 1.2 value of the function and the x = 3.3 value of the function?  What do you get if you multiply this difference by the width of one of the subintervals?

The volume of an sandpile isV = .8 h^3.  h is the altitude of the pile, and h is a function of t. 

What is dV/dh?

What is the expression for dV/dt?

If h is changing at rate 24, then at what rate is V changing?

What does the graph of a function look like at a point where each of the following applies:

the derivative goes from negative to zero to positive,

the derivative from positive to zero to negative

the derivative from positive to zero to positive

the derivative from negative to zero to negative.

What can you say about the behavior of the second derivative in each of the following situations:

the derivative goes from negative to zero to positive,

the derivative from positive to zero to negative

the derivative from positive to zero to positive

the derivative from negative to zero to negative.

Find the first derivative of e^(-3 x^2), where k is a constant positive number.  List the rules you use and show the details of every step.

Find the second derivative of e^(-3 x^2).  List the rules you use and show the details of every step.

In terms of the graph of this function:

What does it mean for the first derivative to be positive at a point? 

What does it mean for the first derivative to be negative? 

What does it mean for the first derivative to be zero? 

What does it mean for the derivative to go from positive to zero to negative, or from negative to zero to positive?

At what point(s) is the derivative of this function zero?  At each such point, determine whether the derivative goes from negative to zero to positive, from positive to zero to negative, or from positive to zero to positive, or from negative to zero to negative, and describe the graph at the point.

At each point where the derivative is zero, what is the value of the second derivative, and what does this tell you about the graph?

At what value(s) of x is the second derivative equal to zero? 

At each point where the second derivative is zero, what is the value of the original function and what is the value of its first derivative?  What does this information tell you about the graph of the function at this point?

At point where the second derivative is zero, does the second derivative go from negative to zero to positive, from positive to zero to negative, from negative to zero to negative or from positive to zero to positive?  What does this information tell you about the graph of the function at this point?

Based on the information you have from the function, its first derivative and its second derivative, describe the graph of the function.

In detail, how would each answer you gave above change, and how would the graph change, if the function was e^(- 2 x^2)?