Class 091104

Things you need to know for the test, with some advice:

Here is an overview of things you really need to understand for the upcoming test, as on Class Notes for 091102, with some added advice:

• Definitions of rate, velocity, acceleration.
• Equations of uniformly accelerated motion

Ideally you know how to derive the equations from the definitions of velocity and acceleration, which give you the first two equations, and by eliminating vf from the first two equations to get the third, and eliminating `dt from the first two equations to get the fourth.

You need to know how to identify intervals, and how to identify the quantities v0, vf, a, `dt, and `ds on an interval.

You need apply the algebra of units in all calculations.

• Newton's three laws.
• Definitions of work/energy, KE, impulse, momentum.

Ideally you know how substituting a = F_net / m into the second and fourth equations of uniformly accelerated motion yield the work-KE theorem and the impulse-momentum theorem.

• Work-KE theorem, definition of PE, work-energy theorem

`dPE of a system is defined to be equal and opposite to the work done ON the system by conservative forces

On an interval, you need to be able to identify `dW_NC_ON, `dW_net, `dPE, `dKE, KE_0, KE_f. 

You should know that

`dW_NET_ON = `dKE and

`dW_NC_ON = `dKE + `dPE.

You should be able to use those quantities which are known to make inferences about those which are unknown (e.g., if you've been able to find `dPE and `dKE, you should be able to use these quantities to find `dW_NC_ON).

• Impulse-momentum theorem, conservation of momentum.

On an interval you should be able to identify `dt, F_net, F_net_ave, m v0, m vf, pf, p0, `dp = `d( m v) = m `dv (provided m constant), F_net * `dt or F_net_ave * `dt.

You should be able to relate these quantities using the impulse-momentum theorem

F_net_ave * `dt =  m `dv.

• Vector components from magnitude and angle; magnitude and angle from vector components.

You should know that, provided theta is measured from the positive x axis in the counterclockwise direction:

• R_x = R cos(theta)
• R_y = R sin(theta)
• R = sqrt( R_x^2 + R_y^2)
• theta = arctan(R_y / R_x) (plus 180 deg if R_x is negative)

You should know that a set of vectors is added by adding all the x components to get R_x, adding all the y components to get R_y, and using these components to determine the magnitude R and angle theta of the resultant.

Newton's Law of Universal Gravitation

If point masses m1 and m2 are separated by distance r, then they exert equal and opposite gravitational forces on one another.  The magnitude of the gravitational force is

• F_grav = G * m1 * m2 / r^2,

where G = 6.67 * 10^-11 N m^2 / kg^2.

• The gravitational force on each mass is in the direction of the other.

The above is called Newton's Law of Universal Gravitation.

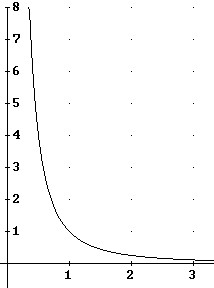
The graph below depicts the curve y = 1 / r^2; you can easily verify the values of y for r = 1/2, 1 and 2, and thereby verify that the curve is correct.

-

This graph can be easily relabeled to represent the force vs. separation curve for any two given masses (e.g., you and the Earth, the Earth and the Moon, the Earth and the Sun, a bowling ball and a baseball, etc.).

Among other things, we can use the above to figure out the orbital velocity of a satellite, in a circular orbit.  To do so requires another general fact about motion in a circle:

If an object moves at constant velocity v around a circle of radius r, its acceleration is

• a_cent = v^2 / r, directed toward the center of the circle.

This is called the centripetal acceleration of the object.

`q001.  The mass of the Earth is about 6 * 10^24 kg.  You should know your own mass (if you want to use your ideal mass, that's OK).  You are about 6400 km from the center of the Earth.

Using Newton's Law of Universal gravitation, find the force exerted by gravity on your mass.

Convert this force to pounds to see if it makes sense.

`q002.  If you were 10% further from the center of the Earth than you are right now, how far would you be?  What force would gravity be exerting on you at that distance?  If you were in free fall at this distance, what would be your acceleration?  What average force do you think gravity would exert on you if you climbed from the surface of the Earth to that distance?  How much would your gravitational PE change during the climb?  Where would you get the energy to manage this?

`q003.  If you doubled your mass, what would happen to the gravitational force exerted on you by Earth's mass?  What would happen to this force if your mass remained unchanged, but Earth's mass doubled?  What would happen if both your mass and that of the Earth doubled?  What would happen if your mass, the Earth's mass and your distance from the center of the Earth doubled?

`q004.  If you drive at 30 mph around a circle of radius 100 feet, what is your centripetal acceleration?  Using your mass, calculate the corresponding centripetal force.

Advice for Test 1

If an object is on an incline:

• Immediately sketch the appropriate force diagram, obtaining the components of its weight parallel and perpendicular to the incline (i.e., mg_x and mg_y, respectively). 
• Note where the parallel component is in the positive or negative x direction. 
• If no other y forces are present, the normal force is equal and opposite to the perpendicular component of the weight, and you should note this.
• If the object moves along the incline, the work done by gravity is done only by the component of the gravitational force which is parallel to the incline (i.e., by mg_x).  Be sure to consider whether the displacement is in the positive or negative x direction, so this result will have the correct sign.  The change in gravitational PE is equal and opposite to the work done on the object by gravity.

A constant-velocity ramp is one on which an object given a velocity down the ramp moves with unchanging velocity.

• Unchanging velocity implies zero acceleration.
• The net force on the object when moving down this ramp is zero, since its acceleration is zero.
• The frictional force and the parallel component of the gravitational force are therefore equal and opposite.  You should draw a force diagram depicting this fact.
• If given a velocity up the ramp, the object will slow.  The frictional force will be down the ramp, still equal in magnitude to the parallel component of the gravitational force.  The magnitude of the net force on the object will therefore be double the magnitude of the force of friction.

Suppose a cart moving down a constant-velocity ramp is accelerated by the weight of a single paper clip, attached to the cart by a string and suspended over a pulley (the string between cart and pulley is parallel to the ramp).  The acceleration of this system is 5 cm/s^2.

• We first do 'ballpark reasoning':  The acceleration of gravity is about 1000 cm/s^2, and the acceleration due to the mass of a single clip is about 5 cm/s^2.  So the cart must be a lot more massive than the clip.  In fact, it's about 1000 / 5 = 200 times more massive.

We then proceed to a more detailed analysis:

• The mass of the system is (m_cart + m_clip). 
• Gravitational and frictional forces on the cart are equal and opposite, so they contribute nothing to the net force.
• The net force is on the system is just the force of gravity on the clip, F_net = m_clip * g = m_clip * 980 cm/s^2.
• The net force on the system is F_net = mass * acceleration = (m_cart + m_clip) * (5 cm/s^2).
• Thus

m_clip * 980 cm/s^2 = (m_cart + m_clip) * (5 cm/s^2), so

(m_cart + m_clip) = m_clip * 980 cm/s^2 / (5 cm/s^2) = 196 * m_clip, and

m_cart = 196 * m_clip - m_clip = 195 * m_clip,

i.e., the mass of the cart is equivalent to the mass of 195 clips.

• If we assume that m_clip is negligible compared to m_cart, our result will be slightly different:

m_cart = m_clip * 980 cm/s^2 / (5 cm/s^2) = 196 m_clip,

i.e., we conclude that the mass of the cart is equivalent to that of 196 clips, rather than 195 clips.

For most purposes we would consider the difference in the two results to be insignificant, and would therefore accept the simpler solution, where the cart has 196 times the mass of a clip.

We might be asked to find the acceleration of this system under various circumstances:

• If we replace the single clip by 7 clips, the net force becomes 7 times as great.  If we regard the mass of 7 clips as insignificant, we conclude that since about the same mass is being accelerated by 7 times the force, the acceleration must be about 7 times as great.  So the acceleration would be 7 * 5 cm/s^2 = 35 cm/s^2.
• If we are asked for the effect of a single clip on a cart of twice the mass, we conclude that the same net force on double the mass will result in half the acceleration, so the acceleration is 1/2 * 5 cm/s^2 = 2.5 cm/s^2.
• If asked about the effect of, say, 3 additional clips on a system with 4 times the mass, we first reason that 3 additional clips on the same mass results in three times the acceleration, or 3 * 5 cm/s^2 = 15 cm/s^2.   If the cart is then given 4 times the mass, we get 1/4 the acceleration, or 1/4 * 15 cm/s^2 = 3.75 cm/s^2.
• If asked what would happen if the mass of the clips was equal to the mass of the cart, it should be clear that we can no longer neglect the contribution of the mass of the clips to the mass of the system.  The mass of the system is double the original mass of the cart, gravity contributes a net force equal to the weight of the cart, and the acceleration of the system is therefore half the acceleration of gravity. 

`q005.  A ball rolls with unchanging velocity down a constant-velocity ramp.  When given a velocity up the ramp its acceleration is -20 cm/s^2.  What is the coefficient of rolling friction between ball and ramp?  What would be the acceleration of the ball if the ramp was perfectly level?  (Apply the advice given previously to these situations). 

`q006.  What would be `dPE, `dKE and `dW_NC_ON for a 100 gram ball as it rolls 40 cm down the constant-velocity ramp of the preceding?  Answer the same if the ball rolls 40 cm up that incline.  Answer the same if it rolls 40 cm along the same ramp, but with the ramp perfectly level.

Homework:

Your label for this assignment: 

ic_class_091104

Copy and paste this label into the form.

Answer the questions posed above.

You should know everything in the first six problems of Set 5 in the Introductory Problem Set, which will give you a good, and not difficult, introduction to working with vectors.  A link that should get you there is at http://vhmthphy.vhcc.edu/ph1introsets/default.htm . 

You should also read Chapters 7 in your text, which can serve as a good coherent reference.