class 091109

Class 091109

Radian measure of angle

The idea of a radian: A radian is an angle such that the arc distance along a circle of radius r is equal to r. You should have a copy of the picture in your notes.

Specific definition: A radian is an angle theta such that the arc length of the sector of a circle of radius r, subtended by the angle theta, is equal to the radius. This definition uses words and phrases students are unlikely to have been required to understand in secondary education within the U.S..

Since writing that definition I've looked up the Wikipedia definition, which says the same thing a little more succinctly: One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.

The radius of a circle is 2 pi r, which means that if you chop the circle up into arcs of length r, there will be 2 pi of them. 2 pi is about 6.28, so a radian corresponds to a little less than 1/6 of the complete circle.

There are 360 degrees around a circle (in polite society we would talk about an arc subtended ... etc.), so we have

2 pi radians = 360 degrees,

from which it follows that

1 radian = 180 / pi degrees and

1 degree = pi/180 radian.

Strap and dominoes

You observed a strap rotating on a die, to rest. You estimated its angular displacement in degrees and the time required to come to rest.

You used your data to calculate the average angular velocity of the strap, in radians / second, for the trial in which you thought the average angular velocity was greatest, and the dominoes stayed on the strap.

Results for omega_Ave, the average angular velocity, ranged from about 1 rad/s to 4 rad/s. The median was around 2 rad/s.

Assuming uniform angular acceleration (which is questionable but not a bad place to start) it is easy to infer the initial angular velocity. In the case of omega_Ave = 2 rad/s, the initial angular velocity would be 4 rad/s.

The question was posed:

If the angular velocity is 4 rad/s, then if the domino is 14 cm from the axis of rotation, how fast is it moving?

The answer is easily reasoned out:

At a distance of 14 cm from the axis, the domino travels in a circle with radius 14 cm. On this circle, each radian of angle corresponds to an arc distance equal to the radius, in this case to an arc distance of 14 cm. So 4 radians would correspond to 4 * 14 cm = 56 cm, and 4 rad/sec corresponds to a speed of 56 cm / sec.

This leads to another question:

What is the centripetal acceleration of the domino?

The domino moves on a circle of radius 14 cm at 56 cm/s, so its centripetal acceleration is

a_cent = v^2 / r = (56 cm/s)^2 / (14 cm) = 220 cm/s^2, approx..

You also estimated the coefficient of static friction by estimating the slope of the strap at which the stationary domino begins to slide. Most estimates were around 1/4 or 1/3. A reasonable estimate of the coefficient of friction (which is equal to the slope at which the domino begins to slide) is therefore .3.

So now we ask:

Is a centripetal acceleration of 220 cm/s^2 consistent with mu_static = .3?

This is easy to answer. Let m stand for the mass of the domino. Then

The strap is horizontal so the normal force and weight of the domino are equal and opposite; normal force is therefore m g = m * 980 cm/s^2.
The force of static friction can therefore be anything up to .3 * normal force = .3 * m g = .3 * m * 980 cm/s^2 = m * 290 cm/s^2, approx.; i.e.,
f_static <= m * 290 cm/s^2.
A centripetal acceleration of 220 cm/s^2 implies that static friction is

f_static = m * 220 cm/s^2

The two conditions are consistent. f_static <= m * 290 cm/s^2 allows f_static = 220 cm/s^2.

Some average angular velocities were as great as 3 rad/s.

This would lead to initial angular velocity 6 rad/s, angular velocity 84 cm/s, and the conclusion that a_cent = v^2 / r = 500 cm/s^2.

This would require force f_static = m * 500 cm/s^2, which is not compatible with f_static <= m * 290 cm/s^2.

This doesn't necessarily imply bad observations; it could result from the assumption of constant acceleration when acceleration is not constant. Since the torque that slows the strap is frictional in nature, this is entirely plausible. So if you got average angular velocity around 3 rad/s, or even 4 rad/s, you at least have a plausible excuse.

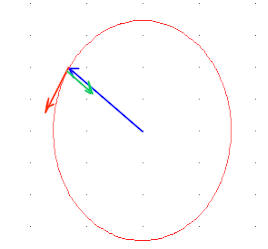
Three vectors for motion on a circle

The figure below depicts a circle. At any instant the motion of an object moving at constant speed around the circle can be characterized by three vectors.

The first vector starts at the center of the circle and terminates at the point on the circle which coincides with the object's position. This is called the position vector and is designated by r or, to emphasize the fact that position is a function of clock time t, by the functional expression r(t). This vector is depicted in the figure by the blue arrow. It is often called the 'radial vector'.
The second vector represents the velocity of the object, and is designated by v or v(t). This vector is tangent to the circle (if the centripetal force suddenly ceased 'holding' the object in its circular path, this is the direction in which the object would then 'fly off', at least until some other force came along and diverted or stopped it). Note that the fundamental geometry of a circle implies that the tangent vector is perpendicular to the radial vector, so the velocity vector v is perpendicular to the radial vector r. This vector is depicted by the red arrow.
The third vector represents the centripetal acceleration. Remember that 'centripetal' means 'toward the center'. So the centripetal acceleration vector is directed toward the center of the circle, and is hence opposite in direction to the radial vector. It is represented by the green arrow in the figure.
The arrows in this figure can be used, with no change, to represent to scale a circle of any size, with any velocity. The three vectors measure three different quantities (displacement, velocity, acceleration) with three different units (e.g., m, m/s, m/s^2), so their lengths represent three completely different quantities, which cannot be measured to the same scale. That is, each quantity (position, velocity, acceleration) has its own scale, and the scale on which one vector is measured is completely independent of the scale of another.

You need to be able to draw this picture for an object at any position on a circle. The only requirements are that the radial vector starts at the origin and ends at the point in question, the other two originate at that point, the velocity vector be perpendicular to the radial vector (therefore tangent to the circle), and the centripetal acceleration vector point back toward the origin.

`q001. It isn't shown, but assume there is an x-y coordinate system in the figure above, with the origin at the center of the circle and the x axis horizontal and directed to the right. This will be the 'official' set of coordinate axes for the figure.

Assume the angle of the r vector with the positive x axis is 230 deg.

Sketch a copy of the figure, include the x-y axes and label that angle. Label the r, v and a_cent vectors.

Now sketch an 'auxiliary', non-official set of x-y axes from the point on the circle. Orient these axes parallel to the 'official' axes. When sketched according to this instruction, the origin of the 'auxilary' axes will be at the terminal point of the r vector (i.e., at the end of the r arrow), and at the initial point of the v and a_cent vectors.

As measured counterclockwise from the positive x axis of the auxiliary system, what is the angle of the v vector?
****

The r vector is at 230 deg counterclockwise from the positive x axis.

The v vector is rotated 90 deg counterclockwise from the direction of the r vector, so the v vector is at 230 deg + 90 deg = 320 deg.

&&&&
As measured counterclockwise from the positive x axis of the auxiliary system, what is the angle of the a vector?
****

The a vector is in the direction opposite that of the r vector. This puts it at 180 deg to the r vector.

230 deg + 180 deg = 410 deg, which is 50 deg beyond 360 deg in the counterclockwise direction. So the a vector makes an angle of 50 deg with the positive x axis.

Alternatively, you could get to the a vector with a -180 deg rotation relative to the r vector, putting you at 230 deg - 180 deg = 50 deg. For a 180 deg rotation, it doesn't matter whether you go clockwise or counterclockwise; you end up at the same angular position.

&&&&

`q002. Sketch the analogous figure, this time with the angle of the r vector at 290 degrees. Give the angles of the v and a vectors, as measured counterclockwise from the positive x direction.

****

The v vector is at 90 degrees to the r vector, putting it at

290 deg + 90 deg = 380 deg,

which is 20 deg counterclockwise from the positive x axis.

The a vector is at 290 deg + 180 deg = 470 deg, which is 470 deg - 180 deg = 110 deg counterclockwise from the positive x axis.

&&&&

Now that we have this picture we can proceed to describe angular motion, the motion of a satellite in circular orbit around a planet, and simple harmonic motion.

Consider a satellite orbiting the Earth, in a circular orbit at distance r from the center of the Earth.

This orbit can be represented by the circle of the above figure. At any point we can sketch vectors representing the radial vector r and the velocity and centripetal acceleration vectors v and a_cent.

Suppose its speed is v and the radius of the orbit is r.

`q003. What is the centripetal acceleration of the satellite?

If its mass is m_sat, then what is the centripetal force accelerating it toward the center of the circle?

****

The centripetal acceleration is

a_cent = v^2 / r,

directed toward the center of the circle.

The centripetal force is therefore

F_cent = m_sat * a_cent = m_sat * v^2 / r.

&&&&

`q004. What is the source of the centripetal force?

****

The source of the centripetal force is the gravitational attraction of the satellite toward the Earth.

&&&&

The centripetal force is just the gravitational force attracting the satellite to the Earth.

This force is expressed in terms of Newton's Law of Universal Gravitation as

F = G * m_earth * m_satellite / r^2.

The centripetal force is m_sat * v^2 / r.

`q005. Set the expression for the gravitational force equal to the expression for the centripetal force. Solve for v.

Show your equation and explain the steps of the solution for v.

****

The equation would be

G * m_earth * m_sat / r^2 = m_sat * v^2 / r. Multiplying both sides by r we get

G * m_earth * m_sat / r^2 * r = m_sat * v^2 / r * r, which simplifies to

G * m_earth * m_sat / r = m_sat * v^2. Dividing both sides by m_sat we get

1 / m_sat * G * m_earth * m_sat / r = 1 / m_sat * m_sat * v^2, which simplifies to

G * m_earth / r = v^2. Taking the square root of both sides,

v = sqrt( G * m_earth / r).

&&&&

`q006. You have your expression for v, the speed of the satellite (you should have obtained v = sqrt( G * m_Earth / r) ).

What therefore is the expression for the kinetic energy of the satellite?

****

KE = 1/2 m v^2. The mass of the satellite is m_sat so we have

KE = 1/2 m_sat * (sqrt( G * m_earth / r) )^2, which simplifies to

KE = 1/2 G * m_sat * m_earth / r

&&&&

A lot of students have been using the formula PE = m g h, whether it is appropriate or not. There are cases where this formula is appropriate, but the present context isn't one of them. The acceleration of gravity isn't even constant as you move from one distance (relative to the center of the Earth) to another, and from the surface of the Earth to the distance of an orbit this acceleration can change very significantly.

The only definition recognized in this course is

`dPE is equal and opposite to the work done by the conservative force on the system.

You actually need calculus to find the expression for the PE of a circular orbit. (Calculus-literate students will confirm that 1 / r^2 is the derivative with respect to r of -1/r, and that once you know a little calculus this is very easy to verify). You don't need to know that, but ask someone who does know a little calculus if it isn't so. This fact is behind the formula for the gravitational PE relative to infinity (again at this point you don't have to know what that means) of masses M and m:

PE = -G M m / r,

which applied to the present situation is

PE = -G * m_earth * m_sat / r.

In the following question, note that G = 6.67 * 10^-11 N m^2 / kg^2, and the radius of the Earth is 6400 km.

`q007. For a person of mass 75 kg, orbiting at a distance of 4 Earth radii from the center of the Earth:

What is the velocity of the orbit?
What therefore is the person's KE when in orbit?
What is the person's PE when in orbit?

****

As we saw earlier the velocity of a circular orbit is

v = sqrt( G * m / r).

In this case m is the mass of the Earth and r is the radius of the orbit, which is 4 * 6400 km = 25 600 000 m (2.56 * 10^7 meters).

Thus

v = sqrt( 6.67 * 10^-11 N m^2 / kg^2 * 6 * 10^24 kg / (2.56 * 10^7 m) )

= sqrt( 1.6 * 10^7 (N m^2 / kg^2 * kg) / m)

= 4 * 10^3 m/s

The units calculation: sqrt( (N * m^2 / kg^2 * kg) / m) = sqrt(kg m/s^2 * m^2 * kg / (kg^2 * m) ) = sqrt( m^2 / s^2) = m/s.

KE is 1/2 m v^2 = 1/2 * 75 kg * (4 * 10^3 m/s)^2 = 6 * 10^8 J, approx.

PE is - G * m_earth * m_person / r

= - 6.67 * 10^-11 N m^2 / kg^2 * (6 * 10^24 kg) * (75 kg) / (4 * 6.4 * 10^6 m)

= -1.2 * 10^9 J, approx..

Note that the magnitude of the PE is 1.2 * 10^9 J = 12 * 10^8 J, which is double the magnitude of the 6 * 10^8 J kinetic energy.

This is what we expect, since

KE = 1/2 G * m_earth _ * m_sat / r and

PE = - G * m_earth * m_sat / r.

&&&&

For the same person sitting in a chair on the ground, what are the values of PE and KE?

****

On the ground, sitting in a chair, v = 0 so KE = 0.

On the ground the distance from the center of the Earth is 6400 km = 6 400 000 m = 6.4 * 10^6 m, so

PE = - G * m_earth * m_person / r

= - 6.67 * 10^-11 N m^2 / kg^2 * (6 * 10^24 kg) * (75 kg) / (6.4 * 10^6 m)

= -4.7 * 10^9 J, approx..

Error alerts:

Students often expect that PE = 0 at the surface of the Earth. This is probably related to the PE = m g h formula, which is one of the reasons I choose not to use this formula very much, preferring to use the definition of `dPE.

Measured relative to infinite separation (which is the only simple reference point for PE between two gravitational bodies), PE = - G * m_earth * m_person / r, where r is the person's distance from the center of the Earth. In this context PE at the surface of the planet is not zero.

It's worth noting that relative to infinite separation, PE is always negative. At the surface of the Earth an object is a lower PE than if it is in orbit, simply because in moving from surface to orbit gravity does negative work on the object, implying that PE increases. The PE at both places is negative, but at the surface of the Earth it's more negative.

To understand the idea of negative PE, you might think in terms of a person climbing up or down a well. Relative to your position on the ground, anyone down the well has negative PE. The further the person is down the well, the lower the PE. If the person climbs upward from one point to another, PE increases (while still remaining negative) so `dPE is positive, even though the PE at both points is negative.

Similarly if you were very far from the Earth, then relative to your position the PE of any mass would be negative; but if the mass moves away from the center of the Earth it experiences a positive change in PE.

For another example of a quantity having a positive change while remaining negative, think of the temperature changing from -20 degrees to -5 degrees. The quantity remains negative but the change is positive.

It is not infrequent for a student to calculate the KE of the person sitting in the chair on the surface of the Earth in terms of the orbital velocity that would apply to an orbiting object at this distance from the center.

A person sitting in a chair on the surface of the Earth isn't in orbit. With that much KE, a person on the surface would be moving so fast that the person would be vaporized as a result of the thermal energy generated by air friction.

Sitting in a chair your KE with respect to the surface of the Earth is zero; even if you use the 300 m/s velocity we have with respect to the center of the Earth, the KE is so much smaller than orbital KE, or the PE changes from surface to orbital distance, that it's essentially zero.

&&&&

What therefore is the change in the person's PE, the change in the person's KE, and the total energy required to get him or her into that orbit?

****

PE changes from -4.7 * 10^9 J to -1.2 * 10^9 J. The change is

`dPE = PE_f - PE_0 = -1.2 * 10^9 J - (-4.7 * 10^9 J) = +3.4 * 10^9 J.

KE changes from 0 to 6 * 10^8 J, a change of

`dKE = KE_f - KE_0 = 6 * 10^8 J - 0 J = 6 * 10^8 J..

The change in total energy is therefore

`dE_tot = `dPE + `dKE = 3.5 * 10^9 J + 6 * 10^8 J = 4.1 * 10^9 J.

It's also useful to be able to think of these in terms of standard prefixes. For example the PE and KE of the orbit are are -1.2 gigaJoules and .6 gigaJoules, respectively.

&&&&

Gasoline has a chemical potential energy of about 100 million Joules per gallon (actually somewhat less than that, but let's use 100 million Joules as a ballpark figure). How much gasoline would it take to supply enough energy to get this person into that orbit?

****

It's worth thinking about the orders of magnitude involved:

100 million Joules is 10^8 Joules.

10 gallons would supply 10^9 Joules.

So it would take the energy of about 41 gallons of gasoline to get someone into orbit.

&&&&

If you could convert the energy from the gasoline's chemical PE into the person's PE and KE, then you could get the person into orbit. However the gasoline wouldn't have enough energy to get both the person and the gasoline itself into orbit. Show that this is so.

****

Gasoline is a little less dense than water (gasoline floats).

A gallon of water weighs about 8 lbs, so the mass of the gallon is about 4 kg.

A gallon of gasoline has a mass of about 3 kg, so 41 gallons has a mass of about 120 kg.

The chemical PE in the gasoline will get 75 kg into orbit; but it certainly won't get its own 120 kg into orbit as well (note that it needs to get all of its mass into orbit, since it would be burning gasoline on the way). It doesn't have enough energy to get even half its mass, in addition to the person's mass, into orbit. The analysis of this process requires calculus, so is beyond the scope of this course, but it should be clear that there are complications involved in providing the energy to get a mass into orbit.

&&&&

So gasoline wouldn't work. And nobody in their right mind would ride a gasoline-powered rocket. Way too explosive and hard to control. Besides, it doesn't burn in a way that ejects the combustion products at high enough speed to make an really fast rocket. There are other chemical combinations that carry more energy per unit of mass. However there are no chemical fuels that have enough energy to even get their own mass into orbit. This is why we use multi-stage rockets to achieve orbit.

Homework:

Your label for this assignment:

ic_class_091109

Copy and paste this label into the form.

Answer the questions posed above.

You have already seen most of the ideas in the qa's and Introductory Problem Set mentioned below. If you work through these documents as assigned, you will get plenty of practice and should develop good expertise with these concepts.

Do qa's #24 and 27 on centripetal force and gravitation.

It won't be assigned until next time, but consider doing qa #29 on radian measure and angular motion:

http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/ph1/ph1_qa_29.htm

Introductory Problem Set 7 consists of 12 problems on gravitation. You will be expected to work through these problems by the first of next week. http://vhmthphy.vhcc.edu/ph1introsets/default.htm .