class 091109

Class 091109

Radian measure of angle

The idea of a radian: A radian is an angle such that the arc distance along a circle of radius r is equal to r. You should have a copy of the picture in your notes.

Specific definition: A radian is an angle theta such that the arc length of the sector of a circle of radius r, subtended by the angle theta, is equal to the radius. This definition uses words and phrases students are unlikely to have been required to understand in secondary education within the U.S..

Since writing that definition I've looked up the Wikipedia definition, which says the same thing a little more succinctly: One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.

The radius of a circle is 2 pi r, which means that if you chop the circle up into arcs of length r, there will be 2 pi of them. 2 pi is about 6.28, so a radian corresponds to a little less than 1/6 of the complete circle.

There are 360 degrees around a circle (in polite society we would talk about an arc subtended ... etc.), so we have

2 pi radians = 360 degrees,

from which it follows that

1 radian = 180 / pi degrees and

1 degree = pi/180 radian.

Strap and dominoes

You observed a strap rotating on a die, to rest. You estimated its angular displacement in degrees and the time required to come to rest.

You used your data to calculate the average angular velocity of the strap, in radians / second, for the trial in which you thought the average angular velocity was greatest, and the dominoes stayed on the strap.

Results for omega_Ave, the average angular velocity, ranged from about 1 rad/s to 4 rad/s. The median was around 2 rad/s.

Assuming uniform angular acceleration (which is questionable but not a bad place to start) it is easy to infer the initial angular velocity. In the case of omega_Ave = 2 rad/s, the initial angular velocity would be 4 rad/s.

The question was posed:

If the angular velocity is 4 rad/s, then if the domino is 14 cm from the axis of rotation, how fast is it moving?

The answer is easily reasoned out:

At a distance of 14 cm from the axis, the domino travels in a circle with radius 14 cm. On this circle, each radian of angle corresponds to an arc distance equal to the radius, in this case to an arc distance of 14 cm. So 4 radians would correspond to 4 * 14 cm = 56 cm, and 4 rad/sec corresponds to a speed of 56 cm / sec.

This leads to another question:

What is the centripetal acceleration of the domino?

The domino moves on a circle of radius 14 cm at 56 cm/s, so its centripetal acceleration is

a_cent = v^2 / r = (56 cm/s)^2 / (14 cm) = 220 cm/s^2, approx..

You also estimated the coefficient of static friction by estimating the slope of the strap at which the stationary domino begins to slide. Most estimates were around 1/4 or 1/3. A reasonable estimate of the coefficient of friction (which is equal to the slope at which the domino begins to slide) is therefore .3.

So now we ask:

Is a centripetal acceleration of 220 cm/s^2 consistent with mu_static = .3?

This is easy to answer. Let m stand for the mass of the domino. Then

The strap is horizontal so the normal force and weight of the domino are equal and opposite; normal force is therefore m g = m * 980 cm/s^2.
The force of static friction can therefore be anything up to .3 * normal force = .3 * m g = .3 * m * 980 cm/s^2 = m * 290 cm/s^2, approx.; i.e.,
f_static <= m * 290 cm/s^2.
A centripetal acceleration of 220 cm/s^2 implies that static friction is

f_static = m * 220 cm/s^2

The two conditions are consistent. f_static <= m * 290 cm/s^2 allows f_static = 220 cm/s^2.

Some average angular velocities were as great as 3 rad/s.

This would lead to initial angular velocity 6 rad/s, angular velocity 84 cm/s, and the conclusion that a_cent = v^2 / r = 500 cm/s^2.

This would require force f_static = m * 500 cm/s^2, which is not compatible with f_static <= m * 290 cm/s^2.

This doesn't necessarily imply bad observations; it could result from the assumption of constant acceleration when acceleration is not constant. Since the torque that slows the strap is frictional in nature, this is entirely plausible. So if you got average angular velocity around 3 rad/s, or even 4 rad/s, you at least have a plausible excuse.

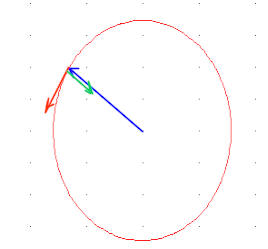
Three vectors for motion on a circle

The figure below depicts a circle. At any instant the motion of an object moving at constant speed around the circle can be characterized by three vectors.

The first vector starts at the center of the circle and terminates at the point on the circle which coincides with the object's position. This is called the position vector and is designated by r or, to emphasize the fact that position is a function of clock time t, by the functional expression r(t). This vector is depicted in the figure by the blue arrow. It is often called the 'radial vector'.
The second vector represents the velocity of the object, and is designated by v or v(t). This vector is tangent to the circle (if the centripetal force suddenly ceased 'holding' the object in its circular path, this is the direction in which the object would then 'fly off', at least until some other force came along and diverted or stopped it). Note that the fundamental geometry of a circle implies that the tangent vector is perpendicular to the radial vector, so the velocity vector v is perpendicular to the radial vector r. This vector is depicted by the red arrow.
The third vector represents the centripetal acceleration. Remember that 'centripetal' means 'toward the center'. So the centripetal acceleration vector is directed toward the center of the circle, and is hence opposite in direction to the radial vector. It is represented by the green arrow in the figure.
The arrows in this figure can be used, with no change, to represent to scale a circle of any size, with any velocity. The three vectors measure three different quantities (displacement, velocity, acceleration) with three different units (e.g., m, m/s, m/s^2), so their lengths represent three completely different quantities, which cannot be measured to the same scale. That is, each quantity (position, velocity, acceleration) has its own scale, and the scale on which one vector is measured is completely independent of the scale of another.

You need to be able to draw this picture for an object at any position on a circle. The only requirements are that the radial vector starts at the origin and ends at the point in question, the other two originate at that point, the velocity vector be perpendicular to the radial vector (therefore tangent to the circle), and the centripetal acceleration vector point back toward the origin.

`q001. It isn't shown, but assume there is an x-y coordinate system in the figure above, with the origin at the center of the circle and the x axis horizontal and directed to the right. This will be the 'official' set of coordinate axes for the figure.

Assume the angle of the r vector with the positive x axis is 230 deg.

Sketch a copy of the figure, include the x-y axes and label that angle. Label the r, v and a_cent vectors.

Now sketch an 'auxiliary', non-official set of x-y axes from the point on the circle. Orient these axes parallel to the 'official' axes. When sketched according to this instruction, the origin of the 'auxilary' axes will be at the terminal point of the r vector (i.e., at the end of the r arrow), and at the initial point of the v and a_cent vectors.

As measured counterclockwise from the positive x axis of the auxiliary system, what is the angle of the v vector?
****

&&&&
As measured counterclockwise from the positive x axis of the auxiliary system, what is the angle of the a vector?
****

&&&&

`q002. Sketch the analogous figure, this time with the angle of the r vector at 290 degrees. Give the angles of the v and a vectors, as measured counterclockwise from the positive x direction.

****

&&&&

Now that we have this picture we can proceed to describe angular motion, the motion of a satellite in circular orbit around a planet, and simple harmonic motion.

Consider a satellite orbiting the Earth, in a circular orbit at distance r from the center of the Earth.

This orbit can be represented by the circle of the above figure. At any point we can sketch vectors representing the radial vector r and the velocity and centripetal acceleration vectors v and a_cent.

Suppose its speed is v and the radius of the orbit is r.

`q003. What is the centripetal acceleration of the satellite?

If its mass is m_sat, then what is the centripetal force accelerating it toward the center of the circle?

****

&&&&

`q004. What is the source of the centripetal force?

****

&&&&

The centripetal force is just the gravitational force attracting the satellite to the Earth.

This force is expressed in terms of Newton's Law of Universal Gravitation as

F = G * m_earth * m_satellite / r^2.

The centripetal force is m_sat * v^2 / r.

`q005. Set the expression for the gravitational force equal to the expression for the centripetal force. Solve for v.

Show your equation and explain the steps of the solution for v.

****

&&&&

`q006. You have your expression for v, the speed of the satellite (you should have obtained v = sqrt( G * m_Earth / r) ).

What therefore is the expression for the kinetic energy of the satellite?

****

&&&&

A lot of students have been using the formula PE = m g h, whether it is appropriate or not. There are cases where this formula is appropriate, but the present context isn't one of them. The acceleration of gravity isn't even constant as you move from one distance (relative to the center of the Earth) to another, and from the surface of the Earth to the distance of an orbit this acceleration can change very significantly.

The only definition recognized in this course is

`dPE is equal and opposite to the work done by the conservative force on the system.

You actually need calculus to find the expression for the PE of a circular orbit. (Calculus-literate students will confirm that 1 / r^2 is the derivative with respect to r of -1/r, and that once you know a little calculus this is very easy to verify). You don't need to know that, but ask someone who does know a little calculus if it isn't so. This fact is behind the formula for the gravitational PE relative to infinity (again at this point you don't have to know what that means) of masses M and m:

PE = -G M m / r,

which applied to the present situation is

PE = -G * m_earth * m_sat / r.

In the following question, note that G = 6.67 * 10^-11 N m^2 / kg^2, and the radius of the Earth is 6400 km.

`q007. For a person of mass 75 kg, orbiting at a distance of 4 Earth radii from the center of the Earth:

What is the velocity of the orbit?
What therefore is the person's KE when in orbit?
What is the person's PE when in orbit?

****

&&&&

For the same person sitting in a chair on the ground, what are the values of PE and KE?

****

&&&&

What therefore is the change in the person's PE, the change in the person's KE, and the total energy required to get him or her into that orbit?

****

&&&&

Gasoline has a chemical potential energy of about 100 million Joules per gallon. How much gasoline would it take to supply enough energy to get this person into that orbit?

****

&&&&

If you could convert the energy from the gasoline's chemical PE into the person's PE and KE, then you could get the person into orbit. However the gasoline wouldn't have enough energy to get both the person and the gasoline itself into orbit. Show that this is so.

****

&&&&

So gasoline wouldn't work. And nobody in their right mind would ride a gasoline-powered rocket. Way too explosive and hard to control. Besides, it doesn't burn in a way that ejects the combustion products at high enough speed to make an effective rocket, and there are other chemical combinations that carry more energy per unit of mass. However there are no chemical fuels that have enough energy to even get their own mass into orbit. This is why we use multi-stage rockets to achieve orbit.

Homework:

Your label for this assignment:

ic_class_091109

Copy and paste this label into the form.

Answer the questions posed above.

You have already seen most of the ideas in the qa's and Introductory Problem Set mentioned below. If you work through these documents as assigned, you will get plenty of practice and should develop good expertise with these concepts.

Do qa's #24 and 27 on centripetal force and gravitation.

It won't be assigned until next time, but consider doing qa #29 on radian measure and angular motion:

http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/ph1/ph1_qa_29.htm

Introductory Problem Set 7 consists of 12 problems on gravitation. You will be expected to work through these problems by the first of next week. http://vhmthphy.vhcc.edu/ph1introsets/default.htm .