Class 091118
Think about the following:
Imagine you're in a car going counterclockwise around a circular path. Is the center of the circle to your right, your left, behind you, in front of you, or none of these? If you slam on your brakes, it what direction do you observe that coffee cup on the seat next to you move? Relative to the circle, in what direction does it move? In what direction does the road surface push the car?
Experiment
Balance a 31-cm ramp (which you should measure accurately) on the edge of a domino, with a stack of dominoes at one end of the ramp. Observe the distance between the balancing point and the nearest edge of the stack.
Repeat of stacks of 1, 2, 3, 4, 5, ... dominoes.
`q001.
For each number of dominoes, give your raw data:
^^^^
&&&&
For each stack, find the distance from the fulcrum (i.e., the domino on which the system is balanced) to the center of the ramp.
The width of a domino is 2.5 cm, length is 5 cm.
Assuming each domino has a mass of 20 grams, find the torque exerted by the stack.
Assuming the full weight of the ramp acts downward from the center of the ramp, use the fact that net torque is zero to find its mass.
For each number of dominoes, give the distance of the middle of the ramp from the fulcrum, then the mass you calculated for the ramp. Use one line for each number of dominoes.
^^^^
&&&&
Explain in detail how you calculated the mass of the ramp for the stack containing 3 dominoes
^^^^
For example, if the balancing point is 8 cm from the 3-domino stack we conclude the following:
- The center of mass of the stack, being 1.25 cm beyond the measured point, lies at 9.25 cm from the balancing point and therefore exerts a torque of - (3 dominoes) * 9.25 cm = -27.75 domino * cm. (a 'domino' of force is the force by gravity on a single domino)
- The end of the ramp is 8 cm + 2.5 cm = 10.5 cm from the balancing point (distance from balancing point to measured point + width of domino = distance of balancing point from end of ramp).
- The center of the ramp therefore lies at 15.5 cm - 10.5 cm = 5 cm from the balancing point, so the torque produced by the weight of the ramp is (ramp weight) * 5 cm.
- The net torque is zero, so
ramp weight * 5 cm = 3 dominoes * 9.25 cm.
Solving we find that ramp weight = 3 dominoes * 9.25 cm / 5 cm = 5.5 dominoes, approx..
The ramp has a weight equal to that of about 5.5 dominoes.
A partial table for one student's work yielded the following approximate results:
# dom dist to edge end to balance cMass to balance mass in dom mass in kg 1 10.5 11.75 2 5.88 0.12 5 5.8 7.05 6.7 5.26 0.11 9 3.5 4.75 9 4.75 0.1
&&&&
What are the sources of uncertainty in this experiment? For which stack do you think the uncertainty in your determination of the mass was least, and what is the basis for your answer?
^^^^
&&&&
Geosychronous satellite
A geosychronous satellite orbits the Earth once per day. The period of the orbit is therefore 24 hours.
We want to find the radius r of this orbit.
Recall that by setting centripetal force equal to gravitational force we find the velocity of a circular orbit of radius r is
The velocity of an orbit is also v = `ds / `dt, where `ds is the distance around the orbit and `dt the time requires to complete an orbit. The circumference of the orbit is 2 pi r so
We therefore have two equations in the unknowns v and r. We can easily solve the equations simultaneously to determine r. Setting our two expressions for v equal, we eliminate v and obtain the equation
which we easily solve for r, obtaining
`q002. What are the radius and velocity of a geosychronous orbit?
^^^^
r = ( G * M_earth * period^2 / (4 pi^2) ) = ( 6.67 * 10^-11 N m^2 / kg^2 * 6 * 10^24 kg * (24 hr * 3600 sec/hr)^2 / (4 pi^2) ) = 43 000 000 m or 4.3 * 10^7 m.
(this is about 6 Earth radii)
v = sqrt( G * M_earth / r) = sqrt( 6.67 * 10^-11 N m^2 / kg^2 * 6 * 10^24 kg / (4.3 * 10^7 m)) = 3000 m/s.
&&&&
Don't do the calculation, but explain how you would use your information to calculate the total mechanical energy (total mechanical energy = PE + KE) of the orbit.
^^^^
KE = 1/2 m_sat v^2, where m_sat is the mass of the satellite.
PE = -G M_earth m_sat / r.
We just solved for v and r, which can easily be substituted into these expressions.
&&&&
Getting used to negative PE
Let's assume that everyone in this discussion has the same mass.
If you are at the bottom of the well and I am at the opening to the well, you will easily come to the conclusion that my PE is greater than yours, since you would have to do work against gravity to get to my position.
You might choose to think that your PE is zero and that mine is positive.
I might choose to think that my PE, since I'm on the surface, is zero and yours is negative.
Either of us would be right, but without a common reference point we would come to very different conclusions about PE.
For example a guy halfway down the well would have negative PE according to my reference point, and positive according to yours. We might agree on how much PE he would lose if he fell to your position, or how much he would gain if he climbed up to mine, but if we want to describe his PE in terms of a single number, we won't be able to do it.
Suppose we agree to use my perspective: PE is zero at the surface of the Earth.
Then the guy halfway down has negative PE, and you have even more negative PE. Both PE's are negative, but yours has the greater magnitude. At the same time your PE is less than his; since your negative number has greater magnitude, it's further 'below zero' than his, so it's less.
Just as we agreed to use the surface of the Earth as the reference point for the example of the well, we need to agree on a reference point for orbital PE. In this case our reference point is 'far, far away'. In fact it's the limit of 'far, far away', an infinite distance.
If we agree to measure PE relative to infinity, then we use the formula PE = - G M m / r. This formula takes care of the fact that g keeps changing (which makes m g h irrelevant since you don't know what value to use for g).
Using this formula everything has negative potential energy. The smaller the value of r, the greater the magnitude of the PE, so things closer to the center of the Earth have a negative PE which less than (but of greater magnitude than) the PE they would have if they were further.
This is analogous to the example of the well. If you're on the surface of the Earth you now have a big negative PE; if you're in orbit halfway to the Moon you have a negative PE but not as big as the one you had on the surface; and to go from a bigger negative PE to a smaller negative PE, your PE has to increase. Put another way, your PE at the surface is 'way below zero'; halfway to the Moon it's still below zero, but not as far below, and to get there your PE must increase.
`q003. Earth's mass is about 6 * 10^24 kg. The Moon's mass is about 1/60 times the mass of the Earth. The two are separated by about 370 000 km.
^^^^
F = G M_earth * m_moon / r^2.
With m_moon = 1/60 M_earth = 1/60 * 6 * 10^24 kg = 10^23 kg and r = 370 000 000 m = 3.7 * 10^8 m, we easily substitute and obtain
F = 3 * 10^20 N.
&&&&
^^^^
The acceleration of the Moon is
a = F_net / m_moon = 3 * 10^20 N / (10^23 kg) = 3 * 10^-3 m/s^2.
&&&&
^^^^
a = F_net / m_Earth = 3 * 10^20 N / (6 * 10^24 kg) = 5 * 10^-5 m/s^2
&&&&
^^^^
The velocity would be
v = circumference / period = 2 pi r / period.
Since centripetal acceleration is a_cent = v^2 / r, we have
v = sqrt( a_cent * r).
Thus
2 pi r / period = sqrt( a_cent * r). Solving for r we get
r = a_cent * period^2 / (4 pi^2). Substituting a = 5 * 10^-5 m/s^2 and period = 28 * 86400 sec, we obtain
r = 6.5 * 10^6 meters,
which is just a little more than the radius of the Earth.
&&&&
^^^^
The forces at 3.7 * 10^8 m and 3.6 * 10^8 m are respectively about 2.9 * 10^20 N and 3.1 * 10^20 N, so the average force is about 3 * 10^20 N.
&&&&
^^^^
The gravitational force on the Moon would act in the direction toward the Earth; since by our assumption the Moon moves toward the earth the work done by gravity would be positive. The displacement is 10 000 000 m, so the approximate work would be
`dW = F_ave * `ds = 3 * 10^20 N * 10 000 000 m = 3 * 10^27 Joules.
&&&&
^^^^
The change in gravitational PE is equal and opposite to the work done by the conservative force. In this case we would get
`dPE = - 3 ^ 10^27 Joules,
approximately.
&&&&
^^^^
Evaluating the PE expression - G M_earth m_moon / r at both distances we obtain
PE at 360 000 000 m is -1.112 * 10^29 J and
PE at 370 000 000 m is -1.081 * 10^29 J.
The difference is about -.03 * 10^29 J = -3 * 10^27 J, in good agreement with our previous approximation.
&&&&
^^^^
As we saw earlier, the Moon's gravitational PE at 370 000 000 m is
PE = -1.081 * 10^29 J.
To move the Moon infinitely far from Earth would require that we increase its PE to 0, since PE is measured relative to infinity.
This would require 1.081 * 10^29 J of energy.
&&&&
^^^^
The Moon's mass is about 10^23 kg and its mass is concentrated at a distance of about 370 000 000 meters from Earth, so its moment of inertia is
I = M R^2 = 10^23 kg * (370 000 000 meters)^2 = 1.4 * 10^40 kg m^2.
&&&&
^^^^
The Moon completes a cycle in about 28 days; a cycle is 2 pi radians.
So its angular velocity is
omega = 2 pi radians / (28 days * 86400 seconds / day) = 2.6 * 10^-6 rad / sec.
&&&&
^^^^
KE = I * omega*2 = 1.4 * 10^40 kg m^2 * (2.6 * 10^-6 rad/sec)^2 = 9 * 10^28 Joules, approx..
&&&&
`q004. What is the velocity of a satellite in a low-Earth orbit at a distance of 7000 km from the center of the Earth?
^^^^
We substitute for G, M_earth and r to get
v = sqrt( G M_earth / r) = 7600 m/s, approx..
Note that the 7000 km radius must be changed to units compatible with the units of G and M_earth in order to get units of m/s.
(Recall that the expression we use here for the velocity is obtained by setting the expression for gravitational force equal to the expression for centripetal force.
&&&&
What are the KE and PE of this orbit?
^^^^
The KE is
KE = 1/2 m v^2 = 1/2 m_sat * (7600 m/s)^2 = 28 000 000 m^2 / s^2 * m_sat,
where m_sat is the mass of the satellite.
The PE relative to infinity is
PE = -G * M_earth * m_sat / r = -56 000 000 m^2 / s^2 * m_sat.
It is worth noting that the magnitude of the KE is half that of the PE, which is the case for circular orbits.
&&&&
If a satellite changes from a circular orbit at 7000 km from the center of the Earth, to a circular orbit at 7001 km, what is `dKE between the orbits and what is `dPE?
^^^^
The work done by gravity on the satellite is approximately equal to the gravitational force multiplied by the 1 km = 1000 m displacement away from the Earth; the force and the displacement are in opposite directions so the work is negative.
The force at 7000 km is
F = G * M_earth * m_sat / r^2 = m_sat * 8 m/s^2.
The work done by gravity is therefore `dW = F * `ds = - m_sat * 8 m/s^2 * 1000 m = - m_sat * 7500 m^2 / s^2.
The change in gravitational PE is, by definition, equal and opposite to this work so we have
`dPE = m_sat * 8000 m^2 / s^2.
The same result could be obtained by substituting r = 7 000 000 m and then r = 7 001 000 m into the formula for PE, and subtracting the first result from the second. It would be necessary to use enough significant figures in the calculation to ensure a few significant figures in the difference.
We could also calculate the velocities at the two distances, use these to find the values of the KE, and subtract (again it is necessary to use a sufficient number of significant figures). The result will turn out to have half the magnitude of the PE change, about
`dKE = -m_sat * 4000 m^2 / s^2.
Note that the negative value of `dKE makes perfect sense, since the velocity necessary to maintain a circular orbit decreases as orbital radius increases.
&&&&
How much work must have therefore be done on the system by nonconservative forces?
^^^^
An object orbiting in a free circular or elliptical orbit in space experiences no nonconservative forces significant to this calculation (though very small nonconservative forces are present and cause a gradual 'decay' of the orbit). So for such an object `dKE + `dPE = 0.
However a freely orbiting object in space cannot change from one circular orbit to another. To do so does require nonconservative forces.
Since `dW_nc_on = `dKE + `dPE, we have
`dW_nc_on = - m_sat * 4000 m^2 / s^2 + m_sat * 8000 m^2 / s^2 * m_sat = +4000 m^2 / s^2 * m_sat
To 'raise' its orbit from 7000 km to 7001 km the satellite would have to 'climb', increasing its PE, as well as slow, which will decrease its KE. The PE increase is greater in magnitude than the KE decrease so a net 4000 m^2 / s^2 * m_sat of energy must be provided by the engines.
&&&&
`q005. The Moon's orbit around the Earth is actually elliptical, with its closest approach occurring around 360 000 km and its furthest distance around 380 000 km.
No significant nonconservative forces act on the Moon in its orbit.
Does the Moon gain or lose KE as it moves from the 380 000 km distance to the 360 000 km distance?
^^^^
We easily calculate the PE at each distance, substituting 380 000 000 m and 360 000 000 m for r in the PE expression -G M_earth m_moon / r and subtracting.
We obtain approximate PE values -1.05 * 10^29 J and -1.11 * 10^29 J, respectively, so
`dPE = -1.11 * 10^29 J - (-1.05 * 10^29 J) = -6 * 10^27 J.
&&&&
How much KE does it gain or lose? (hint: you should start by calculating the Moon's PE at both points; you should not start by assuming that the Moon moves between two circular orbits with radii 380 000 km and 360 000 km)
^^^^
`dKE has half the magnitude, and the sign opposite, the `dPE. Thus
`dKE = 1/2 * 6 * 10^27 J = 3 * 10^27 J.
&&&&
`q006. An object moves around a circle with radius r = 100 cm at velocity v = 50 cm/s and centripetal acceleration a_cent = 25 cm/s^2.
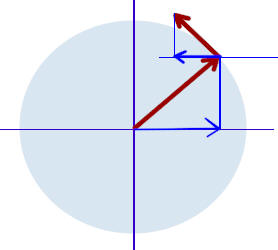
Sketch the radial, velocity and centripetal acceleration vectors corresponding to angular position theta = 45 degrees. Sketch the x component of the radial vector.
Sketch auxiliary axes to determine the directions of the velocity and centripetal acceleration vectors, and using the auxiliary axes sketch the x components of each of these vectors.
Describe your sketch in detail:
^^^^
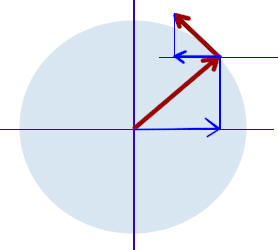
The sketch below depicts the circle, with its interior shaded in light blue, with the radial vector r at about 45 degrees. There is a blue vertical projection line from the end of the vector down to the x axis, and the x projection r_x is depicted, also in blue.
The velocity vector v is tangent to the circle, at angle 45 deg + 90 deg = 135 deg. Both the velocity vector and the radial vector are depicted in red. An auxilary x axis is sketched through the initial point of the velocity vector (the auxiliary y axis has been left off to avoid confusion with the vertial projection line). It should be clear that the angle from the positive auxiliary x axis to the velocity vector is about 90 deg + 45 deg = 135 deg.
There is a projection line from the end of the v vector down to the auxiliary x axis, and the projection vector v_x is depicted, pointing in the negative x direction.
To avoid cluttering the figure the centripetal acceleration vector a_cent is not shown. It points back from the end of the r vector toward the origin, in the direction exactly opposite that of the r vector. Its angle with the positive x direction is therefore 45 deg + 180 deg = 225 deg. The x projection of the a_cent vector will be found using the same auxiliary x axis that was used with the v vector.

&&&&
Estimate the x component of each vector. Give your estimates below.
^^^^
The radius of the circle is 100 cm so the magnitude of the radial vector r is 100 cm. The x projection falls short of the circle, but its length is well over half the radius. An estimate in the neighborhood of 70 - 80 cm would be reasonable.
The vector v_x is clearly shorter than the vector v. Its length is probably 70-80% that of the v vector. 70% of 50 cm/s is 35 cm/s, so an estimate of 35 - 45 cm/s would be reasonable.
The x projection of the a_cent vector will similarly have a magnitude about 70-80% that of the centripetal acceleration. 70% of 25 cm/s^2 is about 18 cm/s^2, so an estimate in the neighborhood of 18 - 20 cm/s^2 would be good.
&&&&
Using sines and/or cosines as appropriate, calculate the x component of each vector.
Give your calculations below
^^^^
Calculating to 2 significant figures we get
r_x = r cos(45 deg) = 100 cm * cos(45 deg) = 71 cm.
v_x = v cos(135 deg) = 50 cm/s * cos(135 deg) = -35 cm/s
a_cent_x = a_cent cos(225 deg) = 25 cm/s^2 * cos(225 deg) = 25 cm/s^2 * (-.71) = -18 cm/s^2.
v_x and c_cent_x are both negative, indicating that these projections are directed to the left. r_x is positive, indicating that this projection is directed to the right. These directions are consistent with our sketch.
&&&&
Repeat for angles theta = 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
List the x components of the radial vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
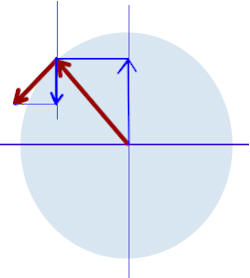
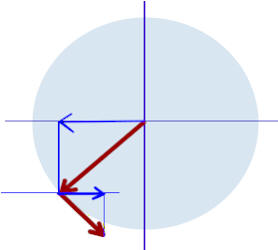
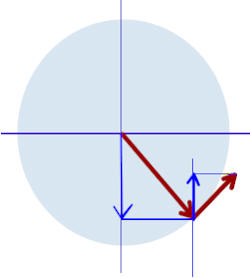
The figures for 135 deg, 225 deg and 315 deg are shown below.
At all these angles the magnitudes of the x components of the three vectors are identical to those for the 45 degree angle (r_x has magnitude 70 cm, v_x has magnitude 35 cm/s and a_cent_x has magnitude 18 cm/s^2). It should be clear from each picture whether the corresponding component is to the right (positive) or left (negative).
At 135 deg the projection r_x would be to the left, v_x would be to the left and a_cent_x would be to the right.
At 225 deg the projection r_x would be to the left, v_x would be to the right and a_cent_x would be to the right.
At 315 deg the projection r_x would be to the right, v_x would be to the right and a_cent_x would be to the left.
The figures for angles 90, 180 and 270 degrees are not shown. However the following results should be clear from your sketches:
&&&&
List the x components of the velocity vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
The x components of the 50 cm/s velocity vector, which are listed progressively as we move around the circle, are
It should be clear from these results that the x projection of the radial vector speeds up, reaches maximum speed, then slows to zero, as it moves to the left. Then it moves to the right, speeding up before reaching maximum speed then slowing once more to 0.
&&&&
List the x components of the centripetal acceleration vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
The x components of the 25 cm/s centripetal acceleration vector, which are listed progressively as we move around the circle, are
&&&&
Can the x component of the position vector have the same sign as the x component of the velocity vector?
^^^^
This is possible:
&&&&
Can the x component of the position vector have the same sign as the x component of the centripetal acceleration vector?
^^^^
&&&&
Can the x component of the centripetal acceleration vector have the same sign as the x component of the velocity vector?
^^^^
This is possible, and occurs at the 45 degree and 225 degree positions.
More generally it happens whenever the radial vector is in the first or third quadrant.
&&&&
Homework:
Your label for this assignment:
ic_class_091118
Copy and paste this label into the form.
Answer the questions posed above.
No new qa's are assigned. Try to catch up.
You should familiarize yourself with text chapters: