Class 091207 draft
Suggested approach to problems:
First list the names, symbols, units and values of the quantities you are given. This helps get your thinking into the context of the situation. Be sure you're using the right words, the right symbols, the right units. The better you do with this, the more clearly you are likely to think about the situation.
Unless it's obvious don't even think about what the question asks you to figure out. Think first about what you can do with the information you have, rather than confining your thinking to a specific goal. Ask yourself what you can figure out from the given information. Use sketches, diagrams, words, etc..
Once you know what you can do with the information, it's time to focus yourself on the goal. This is the time to start thinking about what the question wants you to figure out.
Orbital Mechanics
What quantities are associated with a satellite in circular orbit around a planet?
Given the mass, velocity and orbital radius of a satellite in a circular orbit, what other quantities can we find, and what specific reasoning process do we use?
If we give a quick impulse to a satellite in circular orbit, in the direction of its motion, what can we predict will happen to the shape of the orbit, and to the kinetic, potential and total energies?
Suppose a satellite is in an elliptical orbit. What difference does it make to the shape of the new orbit if a given impulse is delivered at the perigee vs. at the apogee? What difference does it make to the total energy of the new orbit?
Which has greater total energy, a circular orbit or an elliptical orbit which remains inside the circular orbit except at two 'extreme points' where it just touches the circular orbit?
... effects on magnitude and direction of velocity, PE starts increasing etc ... effect on KE is greater if at higher speed ... so greater influence on total energy at higher speed ... if we want to get a circle, though, we're just going to make things worse because the satellite will return to the point at which the impulse was delivered ... note that magnitude of impulse is not a measure of fuel used, since original speed determines energy required for given impulse ... interesting that by firing rockets to increase vel in direction of motion, we can slow down, as long as we fire them at apogee (perigee speed is affected more than apogee speed) ... perigee firing increases eccentricity, apogee decreases
... PE increases because path is no longer perpendicular to radial vector
... do you tend to be early or late in timing the perigee and apogee? your attempt to achieve a circular orbit will tell...
... create an elliptical orbit that reaches r = 3 and brushes r = 1, with the major axis horizontal ...Problem Number 2
During a 6.2 -second time interval, a disk is observed to accelerate from 9.699 radians/second to 12.39 radians/second.
The second sentence also provides information, but we can determine a whole lot from the three quantities given in the first sentence so we stop here and sketch out what we know we can find:
Now the second sentence gives us net torque, which is tau_net = 6 m N. What can we now find?
Net torque is tau_net = I * alpha.
The torque of a force exerted at a point is tau = r X F
tau_net = sum(tau_i) (we get net torque by adding all the individual torques)
We know alpha and tau_net so we can easily find I.
Now would be a good time to ask what the problem wants us to find.
From omega_0, omega_f and `dt we find the acceleration alpha. We get alpha = (omega_f - omega_0) / `dt.
From tau_net = I * alpha we get I = tau_net / alpha.
Evaluating alpha we have alpha = (12.4 rad/s - 9.7 rad/s) / (6.2 s) = (2.7 rad/s) / (6.2 s) = .43 rad/s^2.
Evaluating I we get I = 6 m N / (.43 rad/s^2) = 14 kg m^2.
note: be sure you do the units calculations correctly; these are illustrated in detail in earlier class notes.
Are there aspects of this problem that you could usefully visualize using graphs?
^^^^
A graph of omega vs. t could be useful in determining the angular acceleration and angular displacement, which are respectively the slope of and area beneath the omega vs. t trapezoid.****
`What definitions apply to this situation, and what are the names and symbols for the quantities are involved?
^^^^The definitions of angular velocity and angular acceleration can be used to infer the angular acceleration and angular displacement.
****
`Does this problem involve any of the formulas you have been advised to memorize? What relevant formulas result from definitions and basic laws?
^^^^tau_net = I * alpha is the rotational analog to F_net = m a. It is important that you know both forms of Newton's Second Law.
****
`What situations seem similar to this, but perhaps not exactly the same? What concepts, ideas and procedures have a similar 'feel'?
^^^^The motion 'feels' a lot like linear motion; the behavior of torque and moment of inertia are analogous to the behavior of net force and mass.
****
`What is the nature of the reasoning you use when working through this problem?
^^^^Direct reasoning from definitions is recommended, where it works, in solving problems where acceleration or angular acceleration is uniform.
It is recommended that you use the strategy of listing what is known and what can be determined from what is known.
****
`How have the quantities and relationships used in working out this problem been directly experienced in experiments and other hands-on activities?
Problem Number 3
A tower rises from its base at the surface of the Earth, a distance of 6400 km from the center, and rises an altitude of 900 kilometers above the surface. An individual of mass 87 kg wishes to climb the tower.
We are given the mass of the individual, his initial distance from the center of the Earth and the altitude of the tower. Before reading further figure out what you can do with this information:
We are given a power output of .99 watts per kg of body mass, sustainable for 8 hours.
We need to figure out how much energy is required to climb the tower.
This problem is solved in the Introductory Problem Set.
Are there aspects of this problem that you could usefully visualize using graphs?
^^^^
A graph of gravitational force vs. position on the tower could be useful. The work is the area beneath the graph.****
`Are there things about this problem that you could usefully represent using pictures and/or diagrams?
^^^^A picture of the tower with gravitational force vectors decreasing with height might be very helpful.
****
`What definitions apply to this situation, and what are the names and symbols for the quantities are involved?
^^^^work = ave force * displacement
`dPE is equal and opposite to work done by conservative force
****
`Does this problem involve any of the formulas you have been advised to memorize? What relevant formulas result from definitions and basic laws?
^^^^You probably need Newton's Law of Universal Gravitation.
You need to know that weight is force exerted by gravity.
You might need the expression - G M m / r^2 for potential energy relative to infinity.
****
`What situations seem similar to this, but perhaps not exactly the same? What concepts, ideas and procedures have a similar 'feel'?
^^^^The work here is done by a changing force. In this sense there is a similarity to the work done when stretching an elastic object.
****
Problem Number 8 What is the mass of a planet about which a small satellite orbits with a period of 52 minutes at a distance of 20000 km from the planet's center? Let's first ignore the fact that we're asked for the mass, and figure out what we can do with the given information.We are given the time required for a single orbit and the distance from the center of the planet, which is the radius of the orbit.
Now let's think about the question of mass.
Problem Number 4
As an Earth satellite of mass `mass kg, originally in a circular orbit of radius 7.05 * 10 ^ 6 m, increases its orbital radius to 7.17 * 10 ^ 6 m, what are the KE and PE changes and the ratio of PE to KE change?
The mass, designated by `mass, is not given. The symbol `mass should have been represented as a number. You are free to substitute any number you wish. You could choose 1 kg, a good choice because it simplifies the arithmetic. You are also free to regard `mass as an unknown quantity, and represent your solution in terms of the symbol `mass.
We are given the two orbital radii. For each we could calculate any of the following in terms of the mass `mass:
We are asked to find PE and KE changes.
An ideal spring has restoring force constant 950 Newtons/meter. An unknown mass on the spring is observed to complete 47.616 cycles every minute. What is the unknown mass, in kilograms?
We are given the force constant k = 950 Newtons / meter.We are given the number of cycles completed every minute.
At this point we know the angular frequency omega, and the force constant k. This should call your attention to the formula omega = sqrt( k / m ).
m = omega^2 / k
`Does this problem involve any of the formulas you have been advised to memorize? What relevant formulas result from definitions and basic laws?
^^^^This problem requires the formula omega = sqrt( k / m ), which is to be memorized.
****
Problem Number 7
If 37 J of net work is done on a system while 17 J of work are done on the system by nonconservative forces, then by how much do the PE and the KE of the system change?
This requires only knowledge of the basic work-kinetic energy theorem and the definition of `dPE:
`What definitions apply to this situation, and what are the names and symbols for the quantities are involved?
^^^^We use the definition of `dPE as equal and opposite to the work done on a system by conservative forces.
****
`Does this problem involve any of the formulas you have been advised to memorize? What relevant formulas result from definitions and basic laws?
^^^^We use the basic work-KE theorem `dW_net_on = `dKE.
****
Problem Number 13An object of mass 4 Kg is acted upon by an unknown force F for `dt = 6 seconds. Its velocity is observed to change during this time from 9 m/s to -1017 m/s.
We are given
We can determine a number of quantities from this information:
We are then asked to use the impulse-momentum theorem:
We are asked to also use uniformly accelerated motion:
An object moves around a circle of radius 3 meters, making a revolution every 4.7 seconds. Assume that its angular velocity is constant. Starting at t = 0, when its angular position is 0 radians, what are the x and y coordinates of its position after t seconds (express your answer in terms of the parameter t)?
We are given the radius and time required for 1 revolution around a circle:
We can get of the solution in two different lines of reasoning:
One line of reasoning:
It's important to visualize the motion of the object. Let's think for a minute about how the position of the object changes:
- It will take 1/4 * 4.7 sec = 1.175 sec to reach the 90 degree or pi / 2 position; 1/2 * 4.7 sec = 2.35 sec to get to the 180 deg or pi position, and 4.7 sec to get to the 2 pi position.
- After 1 second it will have traveled through 1 / 4.7 revolutions, after 2 second it have traveled through 2 / 4.7 seconds, after 4.7 sec it will have traveled through 4.7 / 4.7 revolutions = 1 revolution.
- The angular positions corresponding to 1 sec and two sec are 1 / 4.7 * 2 pi rad = 1.34 radians, 2 / 4.7 sec * 2 pi rad = 2.67 rad.
After t seconds it will have traveled through t / T revolutions, so its angular position will be
theta = t / T revolutions = t / T * 2 pi radians.
The radial vector has magnitude 3 m, matching the radius of the circle, so the x and y components of position after t seconds are
- x = 3 m * cos(t / T * 2 pi rad) = 3 m * cos( (2 pi / T) * t)
- y = 3 m * sin(t / T * 2 pi rad) = 3 m * sin((2 pi / T) * t)
Since 2 pi rad / T = 6.28 rad / (4.7 sec) = 1.34 rad / sec, approx., we have
- x = 3 m * cos(1.34 rad/sec * t)
- y = 3 m * sin(1.34 rad/sec * t)
Another line of reasoning:
Given the period T = 4.7 sec we can find the angular frequency omega. It takes 4.7 sec to go around the circle, which corresponds to an angular displacement of 2 pi radians. So the angular velocity of the object is 2 pi rad / (4.7 sec) = 1.34 rad / sec. Formally
omega = dTheta / `dt = 2 pi rad / (4.7 sec) = 1.34 rad / sec.
After t seconds the angular position of the object is
theta = omega * t = 1.34 rad/sec * t.
Once more the radial vector has magnitude 3 m, matching the radius of the circle, so the x and y components of position after t seconds are
- x = 3 m * cos(1.34 rad/sec * t)
- y = 3 m * sin(1.34 rad/sec * t)
Note on a bunch of confusing formulas and why they probably aren't worth memorizing:
Problem Number 15The following formulas all say things that are obvious if you know how to think about motion on the reference circle:
- omega = 2 pi / T, where T stands for the time required to complete a revolution (i.e., the period of the motion) says that angular velocity of a point moving around a circle is 2 pi radians divided by the time required to complete a revolution.
- omega = 2 pi f, where f stands for frequency, says that the angular velocity of a point moving around a circle is 2 pi radians multiplied by the number of times the point goes around the circle in a second.
- f = 1 / T says that the number of times you go around a circle in a second is the reciprocal of the time required to go around the circle (e.g., if it takes .1 second to complete a revolution, then you complete 1 / .1 = 10 revolutions in a second).
- T = 2 pi / omega says that if you divide 2 pi radians by the angular velocity you get the time required to complete a revolution (i.e., if you divide angular displacement by angular velocity you get the time interval).
- f = omega / (2 pi) says that if you divide the number of radians per second by the 2 pi radians around the circle, you get the number of times the object goes around the circle every second. For example at 6 pi radians / sec you go around the circle 3 times in a second.
Most of these formulas include 2 pi, mostly in the numerator though in some cases it's in the denominator. One doesn't have 2 pi at all. T is in the numerator. f is in the denominator except when it isn't. Most people can't keep the formulas straight without understanding their meanings; if the meanings are understood then there's no need to memorize them.
However all these formulas can be reduced to two:
- omega = 2 pi / T
- f = 1 / T.
All the others are just combinations and/or rearrangements of these two. If you need to memorize something, memorize these two. But by all means be sure you understand motion on a circle so you know what they mean.
What is the KE change of an object of mass 7.9 kg as its gravitational PE increases by 65 J if at the same time it also does 49 J of work against the net nongravitational force?
This is a clear application of energy conservation:
Gravitational PE increases by 65 J. `dPE is equal and opposite to the work done by the gravitational force on the object, so the gravitational force does -65 J of work on the object.
The object does 49 J of work against other forces, so the other forces do -49 J of work on it.
The sum of the gravitational and nongravitational forces is the net force (every force is one or the other).
Thus the work done on the object by the net force is -65 J + (-49 J) = -114 J.
That is, `dW_net_on = -114 J.
Since `dW_net_on is equal and opposite to the change in KE, it follows that `dW_net_on = -114 J.
8 levels; online tests on each topic at each level with
feedback, small percent with goal of preparation; proctored exam on
each level (spiral thru topics; e.g. in ph1, motion, forces, Newton's 2d law,
work-energy, impulse-momentum, gravitation,
rotation, shm -- 121 first four levels, 201 first six levels but combine
proctored exams on levels 1-2, perhaps 3-4 so only
4 or 5 tests; 231 combines 1-2, 3-4, 5-6 then tests individually on 7 and 8)
experiments: mass on spring, rotating strap-magnet response to steel object or
magnet (effect on frequency) ... series of
such straps could model wave motion (align several straps with axes all along
same line, 'start' each when previous reaches
equilibrium position ... waves formed by the two ends propagate in opposite
directions(?) ... small amplitude OK, could be
done with pend brackets on tabletop
Speculate on what strategies are required to get a spacecraft to the Moon, which is about 60 Earth radii away, and back. Demo some grav sim exercises (perhaps trying to hit r = 3 orbit from r = 1.02 orbit) and insert questions.
Note that you can if you wish experiment with this situation by following the
instructions for 2d Planet; just be careful to set your original parameters so
that the Moon is visible.
Your answer (start in the next line):
strategy to get to Moon:
your brief discussion/explanation:
************`
-------------
&&&&&&&&&&&&&&&
How about partial credit for 'magic'?
dPE = GMm/r1 - GMm/r2
dPE = (6.67*10^-11Nm)(5.98*10^24kg)(m_shuttle)/6400000m -
(6.67*10^-11Nm)(5.98*10^24kg)(m_shut)/384000000m = mshut(61284100J)
and then just double it coming back?
I feel like I just killed a whole bunch of astronauts with that answer.
are you ready for test qa
break down into thinking pattern
if you quote a formula discuss its meaning
formula sheet: OK to say that 4 pi k = 1 / epsilon_0, stuff like that
not OK to provide formulas for freqency, angular frequency, period, etc. that
follow from one simple idea
not OK to provide formulas that result from PV = n R T; OK to relate R and k
`q007. You should be able to sketch each of the following, as sketched and discussed in class. Give a brief synopsis of the important characteristics of each sketch.
v vs. t graph trapezoid
vector projection (project one vector on another)
vector components on x-y coordinate system (sketched in standard vertical-horizontal position, and in 'rotated' positions)
forces on a ball on an incline without friction
forces on a free pendulum at a position away from equilibrium
addition of two vectors by sketching, adding and resolving components
mass on an incline incline with friction and a suspended mass
atwood machine
v vs. t and x vs. t graphs, interrelationships
circular motion with r, v, a_cent
forces in elliptical orbit
forces on domino on accelerating strap
SHM model
wheel with descending mass
skills thread
reason from definitions (first challenge: object to or from rest given `ds, `dt)
linearity vs. nonlinearity
proportionality
units calculations and conversions; relabeling graphs
algebra of unif accel (deriving the equations, then solving them)
logic of 4 eqns (given 3 can find other two)
vectors
graphs
definitions thread
ave rate, ave vel, ave accel
force
KE, PE, impulse, momentum
gravitational force
moment of inertia, torque, angular velocity, acceleration
simple harmonic motion
theorems/laws thread
Formulas you just need to know (the rest you should be able to reason out) (you should know what each of these means)
a_cent = v^2 / r
omega = sqrt(k/m)
F = G M m / r^2
PE = -G m m / r
formulas you could be excused for memorizing (too much hassle to remember where they came from) (you still have to know the conditions and meanings)
v = sqrt( G M / r)
PE_elastic = 1/2 k x^2
formulas you should be ashamed to have to memorize
v_Ave = `ds / `dt
a_Ave = `dv / `dt etc.
TIMER program
Do the experiment Using the Timer Program , down to the point where you see the instruction that reads as follows (you do not need to follow this instruction):
'You got at least 20 time intervals. Based on your data what was the average of the first 20 time intervals? Note that you could get this average by averaging the first 20 intervals. My first few intervals were .15625, .15625, .1875, .171875, etc; I could just add up the first 20 intervals and divide by 20 to get the average. However there is an easier and quicker way to get the result, so use the easier way if you can.'
Once you get the TIMER program to work, you should be able to run the gravitational simulation program from yesterday's class notes.
Experiment
Using a paperclip to fix the end of a thread in place, wrap the thread at least half a turn around the rim of the foam wheel. Suspend a mass from the other end of the thread, so that when the system is released the mass will be free to descend, with the resulting torque accelerating the wheel.
The figure below indicates a wheel with a blue string wrapped around its rim, from the position of the radial vector r_0 to the position of the radial vector r_hat, then extending a ways downward to a suspended mass. The system is assumed to rotate about an axis through the center of the circle.

The nondescript green shape represents a paperclip attached to the wheel in such a way that the thread will be anchored to the rim of the wheel through the r_hat position, but will slip off not long after reaching that position. The figure below shows a typical position at which the thread slips off: This event (the thread slipping off the clip, which separates the thread and suspended mass from the wheel) will be referred to as 'separation'.
The radial vector at this position is labeled r_sep. (standing for 'radial vector at separation').
Between the r_0 and r_hat positions the thread remains in contact with the rim of the wheel. As long as this is the case, the suspended weight will exert a torque with r_hat as its moment arm, and the magnitude of the torque will be just r_hat * suspended weight. This torque is counterclockwise, hence it is negative so between the two positions we have
- torque = tau = - r_hat * suspended weight.
As the wheel rotates beyond the r_hat position the thread will lose contact with the rim of the wheel but will stay in contact for a short time with the paperclip. The moment arm used to calculate the torque will therefore decrease a bit, but as long as the thread slips off somewhere around the position depicted in the second figure the moment arm will not have decreased too much. So as a first approximation, we can assume that the average torque is tau_ave = -r_hat * suspended weight.
You will set the system up and observe angular position of the r_0 vector. Rest the axis on a relatively low-friction surface (you can just rest it on your fingers if you wish). When you release the system it will accelerate until reaching the r_sep position, and then coast to rest.
`q001. Find the work done on the system by gravity, from the r_sep position to the position at which the wheel comes to rest. If you can solve all or part of this problem without following the prompts below, you may give your solution here. Otherwise answer after the prompts:
^^^^
&&&&
^^^^
&&&&
^^^^
&&&&
&&&&
&&&&
`q002. After the thread slips off the paper clip the system coasts to rest. Consider the interval which extends from the r_sep position until the wheel comes to rest.
^^^^
&&&&
^^^^
&&&&
`q003. We consider again the interval between the r_0 and r_sep positions, the interval on which weight of the descending mass exerts a torque on the wheel. You previously calculated the work done by this torque.
You now have sufficient information to determine the moment of inertia of the system. If you can solve all or part of this problem without following the prompts below, you may give your solution here. Otherwise answer after the prompts:
The KE at that position is 1/2 I omega_init^2, where omega_init is the angular velocity the instant of separation.
^^^^
&&&&
^^^^
&&&&
... next assume that the angular KE is all in the bolts; measure the distances of the bolts from the center and find the mass of a bolt
You have found omega_0
The work done by gravity on the system is equal to the change in the system's KE.
If we set 1/2 I omega_0^2 equal to the
`q004. Determine the PE change of the suspended mass, between the release of the system from rest and the instant of separation. If you can solve all or part of this problem without following the prompts below, you may give your solution here. Otherwise answer after the prompts:
^^^^
&&&&
^^^^
&&&&
^^^^
&&&&
^^^^
&&&&
^^^^
&&&&
^^^^
&&&&
... find net torque during coast to rest ... infer frictional torque and correct initial movement ... repeat expt once more, determining the time for the accel phase and analyze motion for that phase ... do omega_sep results agree for two analyses, energy analysis, etc.?
... what finally do we learn from the semester's experiments?
... do a shm experiment ...
Escape velocity
Consider a projectile 'shot' at high velocity from the surface of the Earth in the radial direction. That is, the projectile is 'shot' directly away from the center of the Earth. We ignore the effect of the atmosphere, which in reality makes this impractical, and we assume that the projectile encounters no forces other than the gravitational force exerted by the Earth.
As the projectile moves away from the Earth, its gravitational PE increases and its KE therefore decreases. The only force acting on it is the force exerted by the Earth, so it encounters no nonconservative forces. It follows from energy conservation that `dPE + `dKE = 0.
We consider the interval between being 'shot' from the surface and coming to rest for an instant before returning to Earth. If the projectile keeps going without returning, then the interval will never end; but in either case the interval begins with the 'shot'.
We will let M be the mass of the Earth, m the mass of the projectile, R the radius of the Earth, and r the distance of the projectile from the center of the Earth.
Since `dKE + `dPE = 0, it follows that if KE + PE > 0 at one point the same is true for all points.
PE at launch, relative to infinite separation, is PE_0 = - G M m / R.
KE + PE at launch is just KE_0 + PE_0 , so
KE + PE > 0 at launch provided KE_0 > = -PE_0
(just subtract PE_0 from both sides of the inequality KE_0 + PE_0 > 0)
KE_0 = 1/2 m v_0^2
PE_0 = - G M m / R
So KE + PE > = 0 provided
1/2 m v_0^2 > = - ( - G M m / R). Solving for v_0 we get
v_0 > = sqrt( 2 G M / R).
`q005. Evaluate the right-hand side of the equation v_0 > = sqrt( 2 G M / R). What is your result?
^^^^
&&&&
If v_0 is greater than your result (even a very little bit greater), then KE + PE > 0 at launch. If KE + PE > 0 at launch, then the same is true until the projectile experiences a nongravitational force. The only force it experiences is that of the Earth, so unless it returns to and crashes into the Earth it will never experience a nongravitational force. Until this happens, if ever, it remains the case that KE + PE > 0.
Can the projectile's PE (recall that in this analysis PE is measured relative to infinite separation from the Earth) ever be positive?
^^^^
&&&&
Since for this case, with v_0 greater than your result, we have KE + PE > 0, is it possible for the projectile's velocity ever to be zero?
^^^^
&&&&
Is it possible for this projectile to ever return?
^^^^
&&&&
`q006. Suppose you are on a merry-go-round, riding a painted pony at a distance of 4 meters from the axis of rotation. What is your contribution to the moment of inertia of the merry-go-round?
^^^^
&&&&
If the merry-go-round requires 12 seconds to complete a revolution, how fast are you moving and what is your angular velocity?
^^^^
&&&&
What is your kinetic energy, based on 1/2 m v^2?
^^^^
&&&&
What is your kinetic energy, based on 1/2 I omega^2?
^^^^
&&&&
Suppose the merry-go-round started from rest and required 20 seconds to get up to its present rate of rotation. Assuming uniform angular acceleration:
^^^^
&&&&
What was the angular acceleration?
^^^^
&&&&
How much of the torque produced by the motor was required to accelerate your mass?
^^^^
&&&&
How much force exerted in your direction of motion did it take to get your mass up to its present speed?
^^^^
&&&&
What is the moment arm from the axis of rotation to your position? If you multiply the force exerted in your direction of motion by this moment arm, what is your result?
^^^^
&&&&
... your contribution to moment of inertia of merry-go-round; all aspects of your motion; the strain you put on the motor; what happens if you step off ... get Dima to drop a ball while going around merry-go-round
`q007. You should be able to sketch each of the following, as sketched and discussed in class. Give a brief synopsis of the important characteristics of each sketch.
v vs. t graph trapezoid
vector projection (project one vector on another)
vector components on x-y coordinate system (sketched in standard vertical-horizontal position, and in 'rotated' positions)
forces on a ball on an incline without friction
forces on a free pendulum at a position away from equilibrium
addition of two vectors by sketching, adding and resolving components
mass on an incline incline with friction and a suspended mass
atwood machine
v vs. t and x vs. t graphs, interrelationships
circular motion with r, v, a_cent
forces in elliptical orbit
forces on domino on accelerating strap
SHM model
wheel with descending mass
skills thread
reason from definitions (first challenge: object to or from rest given `ds, `dt)
linearity vs. nonlinearity
proportionality
units calculations and conversions; relabeling graphs
algebra of unif accel (deriving the equations, then solving them)
logic of 4 eqns (given 3 can find other two)
vectors
graphs
definitions thread
ave rate, ave vel, ave accel
force
KE, PE, impulse, momentum
gravitational force
moment of inertia, torque, angular velocity, acceleration
simple harmonic motion
theorems/laws thread
Formulas you just need to know (the rest you should be able to reason out) (you should know what each of these means)
a_cent = v^2 / r
omega = sqrt(k/m)
F = G M m / r^2
PE = -G m m / r
formulas you could be excused for memorizing (too much hassle to remember where they came from) (you still have to know the conditions and meanings)
v = sqrt( G M / r)
PE_elastic = 1/2 k x^2
formulas you should be ashamed to have to memorize
v_Ave = `ds / `dt
a_Ave = `dv / `dt etc.
.. reference circle terminology
... counting, observing, manipulating, counting, interpreting, predicting
... here is the picture; here are the equations you choose which is simpler
x = A cos(omega t)
v = -omega A sin(omega t)
a = -omega^2 A cos(omega t)
omega = 2 pi f
f = 1 / T
conclude ...
... given x = .2 m * cos( 5 t) find amplitude, freq, period, max vel, etc.. ... vel after 1/8 of period ...
x = A cos(omega t)
v = omega A cos(omega t + 90 deg)
(= omega A cos(omega t + pi/2) = - omega A sin(omega t) )
a = omega^2 A cos(omega t + 180 deg) (= etc.)
... the idea of careful setup then quick and easy collection of data is also important (e.g., for ball on ramp a series of photo detectors would be useful) ...
... the idea ... the pictures ... work through questions ... symbolize what you now know
Things you really should know at this point
You should know the meanings of the following expressions:
`q001. Identify each of the expressions above and explain its meaning.
^^^^
&&&&
`q002. What relationship would you use to find each of the following, and how would use use it?
... isolate 1-step questions
... k can be found from a single point whose position is given relative to equilibrium
Repeat previous experiment
Today you repeated the experiment from last Monday's class, involving the rotating strap with the dominoes and magnets.
Note the following:
Calibrate a rubber band chain using 1 domino, 4 dominoes and the number of dominoes which when suspended stretches your rubber band system to the length used in this experiment.
... find PE of rubber band system, `dPE from release to loss of contact ...
Having completed your observations, you should repeat the analysis of that experiment, as instructed in the 091116 notes, and submit. You may submit only that part of the document; this time use the title 'ic_091116_exp_repeat'.
If you did the entire experiment correctly, including the analysis, you do not need to do this. If you previously analyzed your data correctly but didn't include all trials, you should analyze today's data, but you may just submit a synopsis of your data and your results.
`q001. Sketch a graph of the force stretching your rubber band system, in domino weights, vs. its length in cm. Sketch the straight line you think best fits the data.
What is the slope of your graph, in domino weights per cm?
What is the slope of your graph, in Newtons / m (you may assume that a domino weighs .2 Newton)?
The slope of your straight line was affected by the third point, where the rubber band was stretched to the length used in the experiment. We might get a slightly different result using only the 1- and 4-domino points. What is the slope, based only on these points?
What is the meaning of the slope of this graph?
How does the slope change if you increase the length of the chain?
How does the perceived 'stiffness' of the rubber band system change with increasing chain length?
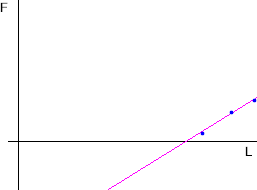
Your F vs. L graph; F vs. x graph
The graph below is similar to that you obtained for F vs. L when you calibrated your rubber band, with the straight line approximately fitting the three data points. (The line has been extended here below the horizontal axis, which would correspond to negative forces; your rubber band chain won't exert forces when its length falls below its unstretched length, so this isn't realistic, but we will soon see examples where this extension of the line is necessary and realistic).
We sketch a vertical line through the horizontal intercept of the straight line:
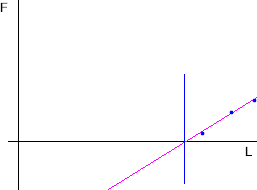
The horizontal intercept is our equilibrium point--the point at which the force exerted by the rubber band system is zero.
It will simplify our analysis to measure horizontal position relative to the equilibrium point.
We will therefore replace our original coordinate system with one whose origin is at this equilibrium point. So we will use our new vertical line as the y axis, and will again label the vertical coordinate F, for force. We will label the horizontal coordinate x.
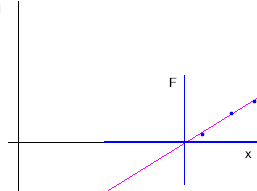
Our x coordinate now represents the horizontal position relative to the equilibrium point. We can now do away with our original y axis, and we obtain the graph below:
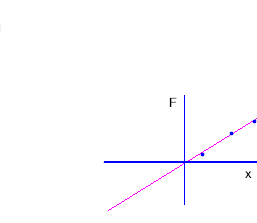
This graph depicts the force exerted by the rubber band as a function of the distance its end is pulled from the equilibrium force. However there is one thing we still need to do to indicate force vs. position. The force exerted by a rubber band at its end is in the direction opposite the direction in which that end is displaced (i.e., if you move the end to the right, the resulting change in the force is to the left; the rubber band 'pulls back' against you).
So in order to depict the force exerted by the rubber band, positive values of position x should be associated with negative forces. Force and position should have opposite signs. So our final graph is as shown below:
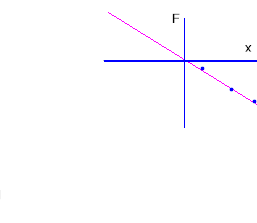
The straight line depicted by the graph goes through the origin. If we denote its slope by -k, then its equation is
F = - k x.
To get the force for position x, we just substitute that value of x into the equation F = - k x and we get the force.
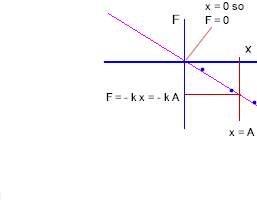
Now let's assume that x has some specific value A:
F = - k x = - k A.
We note that when x = 0 we get F = - k * 0 = 0.
The forces as x = 0 and x = A are indicated on the figure below. The x = A position corresponds to the vertical line labeled 'x = A', and the resulting force is indicated by the vertical projection line:
`q002. We want to determine the work done by the rubber band as we stretch it by moving its end from the equilibrium position to the x = A position. To do so we need to find the average force exerted by the rubber band and the corresponding displacement as we move between the two positions.
... k is force constant ...
... trace themes throughout the course ... direction of force and direction of displacement determine sign of work ... many more themes to be related to experiments, definitions, etc. ... on system vs. by system ...
Experiment
Using the same rubber band chain you calibrated in the preceding experiment, suspend a 4-domino mass, allow the suspended system to oscillate at its natural frequency (being careful that the rubber band never goes slack), and count oscillations for 10 seconds.
`q003. If k is the slope of the force vs. length graph for your rubber band system, and m the mass of the dominoes, then what is omega = sqrt(k / m)?
The units of your calculation should have worked out to 1/s, or s^-1. We aren't going to go into the details of exactly how (it's related to the fact that a meter of arc divided by a meter of radius is a radian), but a radian also appears in the result, and proper unit turns out to be rad / s or rad s^-1.
If a point moves around a reference circle of radius 3 cm, at the angular velocity you just calculated, then what is its speed in cm / s?
What therefore is its centripetal acceleration?
If the reference-circle point represents a mass of .8 kg, then what are the KE of the object, and the centripetal force holding it in its circular path?
If the reference-circle point starts at the positive x axis, then after .1 second, what will be the angle of the r vector?
In the following it is suggested that you sketch the reference-circle figure for each of the given instants, use the figure to estimate the requested quantities, then use sines and/or cosines to refine your estimate with an accurate result:
At the .1 second instant:
Answer the same questions for the instant .2 seconds after the start.
... ref-circle point starts instaneously; nothing with mass can start instantaneously; so how can that happen? point has no mass, of course; but only x component represents position of mass; tracing circle and projection it's clear that the thing starts slowly; vx is of course zero at start ... if y axis, well the actual mass had to be moving already ...
... need picture of circle in multiples of pi/6, pi/4; start by dividing 2 pi by 2.
`q004. One circuit around the reference circle corresponds to an angle of 2 pi radians, or 360 degrees.
How many radians, and how many degrees, would correspond to motion halfway around the reference circle?
How many radians and how many degrees would therefore correspond to motion 1/4 of the way around the reference circle?
... 1 quadrant
How many radians and how many degrees would correspond to motion halfway around the first quadrant? How many degrees and how many radians to 2, 3, 4, 5, 6, 7 and 8 times this angle?
How many radians and how many degrees would correspond to motion 1/3 of the way around the first quadrant? How many degrees and how many radians to 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 times this angle?
`q005. At the angular velocity corresponding to your system, after how many seconds would the reference point be at the 30 deg, 120 deg, 210 deg and 300 deg positions?
Assuming amplitude 3 cm, what would be the y components of the position, velocity and centripetal acceleration vectors at each of these positions?
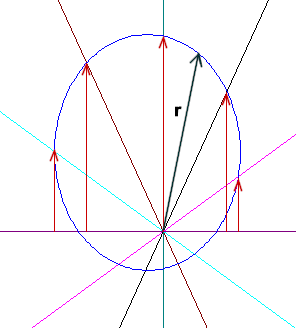
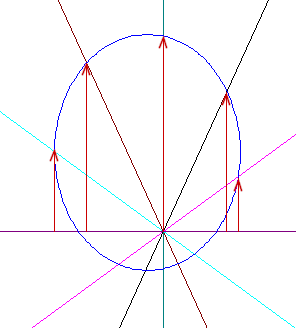
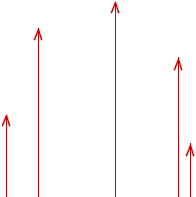
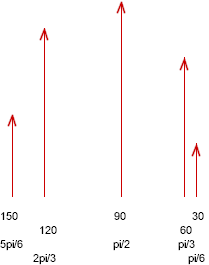
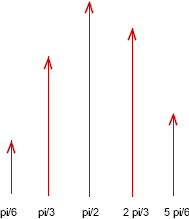
`q006. Sketch a reference circle
... fill in the overall picture of position velocity acceleration ...
... x positions ...
... assume system had amplitude 3 cm, etc.. apply circular model
... net force above and below equil. position
... circle from prev assts give position of pendulum shadowing x position, suspended wt on spring shadowing y position; tell whether moving up or down (rt or left); estimate velocity; tell whether force up or down (rt or left), estimate force as prop of max
Areas of difficulty from previous assignments
units
Reason out the units in each question:
What are the standard units of G M m?
What are the standard units of G M m / r^2?
What are the standard units of G M m / r?
What are the standard units of G M / r?
What are the standard units of G M / r^2?
What are the standard units of tau * omega?
What are the standard units of I * omega?
What are the standard units of I * alpha?
What are the standard units of I * omega^2?
What are the standard units of omega * `dt?
What are the standard units of r * omega?
What are the standard units of alpha * r?
Answer without even thinking about turning on your calculator:
What is 10^-11 * 10^24?
What is 10^-11 / 1 000 000?
What is 10^18 / 10^-11?
What is 10^-11 * 10^24 * 10^22 / 100 000 000^2?
SHM
Work all this out through questions:
Reference circle summary:
For a point moving counterclockwise around a circle, if the angular position of the r vector is theta then
all angles measured counterclockwise from some reference direction (e.g., the positive x axis, though the answer would be the same for any fixed reference direction).
The idea of SHM:
If mass m is subject to net force F_net = - k x then if the object is given an initial velocity and/or pulled away from the reference point and released, its position can be modeled by a point moving around a reference circle with angular velocity omega = sqrt(k / m). The position, velocity and acceleration of the object is the x coordinate of the r, v and a_cent vectors of the reference circle.
Refined statements:
If the motion of an object is the projection on a fixed line of the position of a reference point moving at constant velocity around a reference circle, then that motion is called Simple Harmonic Motion (abbreviated SHM). Usually the fixed line is in the direction of either the x or the y axis, but it need not be so.
If a mass m is subject to a net force of the form F = - k x, then if displaced from equilibrium and released it undergoes simple harmonic motion centered at the equilibrium point. (The same happens if the object, whatever its position, is given a nonzero initial velocity relative to the reference point). The reference point moves around the circle with angular velocity omega = sqrt( k / m ).
The total mechanical energy of the oscillator is the sum of its potential and kinetic energies.
The potential energy of the oscillator at position x is 1/2 k x^2.
The total energy of the oscillator is 1/2 k A^2, where A is the maximum distance of the object from its equilibrium position (A is therefore the radius of the reference circle).
Consequences and observations:
In time interval `dt the reference-circle point moves through angle `dTheta = omega * `dt. If the reference-circle point is on the positive x axis at t = 0, then at clock time t the point is at theta = omega * t. The x component of the r vector is therefore r_x = A cos(omega * t). The velocity vector is at angle omega * t + 90 deg)and the centripetal acceleration vector is at angle omega * t + 180 deg. The speed of the reference point is omega * A and the centripetal acceleration is v^2 / A = (omega * A)^2 / A = omega^2 * A, so the x components are v_x = omega * A cos(omega t + 90 deg) and a_cent_x = omega^2 A cos(omega t + 180 deg).
1/2 k A^2 is the kinetic energy the mass would have if it really moved around the reference circle at angular velocity omega.
If the oscillator is at position x then its PE is 1/2 k x^2; since total energy = PE + KE we can therefore say that 1/2 k x^2 + 1/2 m v^2 = 1/2 k A^2.
The oscillator might be at any position when we choose to start our clock, and unless it is at x = +A or x = -A its velocity could be either positive or negative. If we know the position and whether the velocity is positive or negative, then we know where the point is on the reference circle. The angle of the reference point is
... convert units (e.g., dominoes / cm to N / m)
... pull everything into symbols to summarize
... trace ideas through course
stable and unstable equilibrium: unstable if PE decreases no matter in what direction you move
`q00. At position x = 3 cm a certain pendulum (which is one example of a simple harmonic oscillator) has kinetic energy 4 Joules and potential energy 2 Joules.
What is its PE when it comes to rest at an extreme point of its swing?
What is its KE when it passes through its equilibrium point?
What is its KE at a point where its PE is 5 J?
What is its PE at a point where its KE is 3 J?
... relate all this to a pendulum, then to mass on rb chain
vertical circle
experiment: find slope of force vs. weight for 1 domino, 4 dominoes; find slope of force vs. length graph; find slope of force vs. length graph; use slope to find force corresponding to 3 dominoes; slope is k; slope clearly varies for rb chain so result is only approximate; works only as long as rb length stays within range (e.g., doesn't work if rb goes slack); find work to stretch from 1 to 4 dom; how would work be different if wimpier rb between same #'s of dominoes
k for a certain spring is uniform, and works for compression as well as extension; find force at given positions relative to equilibrium
what is `dPE between equilibrum and max displacement A?
what is PE relative to equilibrium as position x?
spring is attached to mass m; what happens to the position of the end, and what happens when the mass is pulled down another 4 cm and released
neutron star and structural integrity of orbiter
kepler's laws
grinding wheel variation
angular momentum
washer swinging on string; what force constrains; how does force change with freq of rotation
centrip force by pendulum
come back to vertical rotating strap; set up your own and try to detect influence of magnet at greatest possible distance ...
what
Imagine you're in a car going counterclockwise around a circular path. Is the center of the circle to your right, your left, behind you, in front of you, or none of these? If you slam on your brakes, it what direction do you observe that coffee cup on the seat next to you move? Relative to the circle, in what direction does it move? In what direction does the road surface push the car?
moments of inertia of sphere, disk, rod: illustrate by breaking rod into 4 segments (2 each side), then 8 (4 each side); perhaps reference to n segments, Riemann sum -> integral, which in turn is easy
summary/preview of SHM: just how is it that components of velocity vector progress thru 1 rotation; what are x and y components of position vector; what if theta = omega * t
orbital mechanics, energy conservation (very easy if no dissipative forces); comparison of `dPE rel to infinity and `dPE approximated by endpoints of interval
breaking `dPE down into intervals (briefly: Riemann sum etc.)
elliptical orbits, Kepler's Laws
grav sim ...
overview: start with usual picture
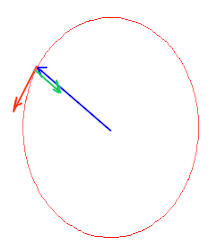
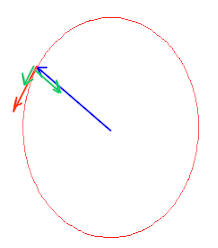
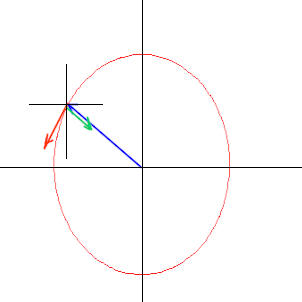
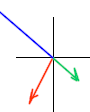
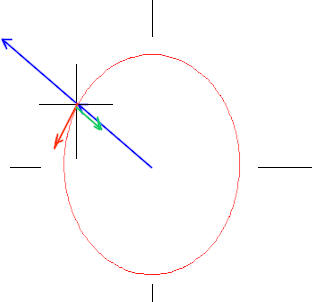
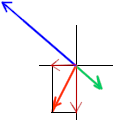
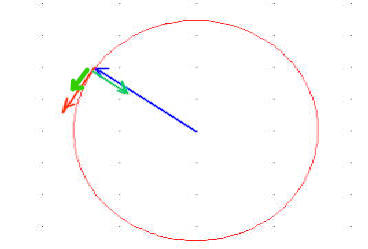
Experiment
Balance a 31-cm ramp (which you should measure accurately) on the edge of a domino, with a stack of dominoes at one end of the ramp. Observe the distance between the balancing point and the nearest edge of the stack.
Repeat of stacks of 1, 2, 3, 4, 5, ... dominoes.
`q001.
For each number of dominoes, give your raw data:
^^^^
&&&&
For each stack, find the distance from the fulcrum (i.e., the domino on which the system is balanced) to the center of the ramp.
The width of a domino is 2.5 cm, length is 5 cm.
Assuming each domino has a mass of 20 grams, find the torque exerted by the stack.
Assuming the full weight of the ramp acts downward from the center of the ramp, use the fact that net torque is zero to find its mass.
For each number of dominoes, give the distance of the middle of the ramp from the fulcrum, then the mass you calculated for the ramp. Use one line for each number of dominoes.
^^^^
&&&&
Explain in detail how you calculated the mass of the ramp for the stack containing 3 dominoes
^^^^
&&&&
What are the sources of uncertainty in this experiment? For which stack do you think the uncertainty in your determination of the mass was least, and what is the basis for your answer?
^^^^
&&&&
center of mass of a ramp loaded with one domino; then loaded with 3 dominoes of nonequal spacing; use to determine mass of ramp in terms of mass of domino; what is ideal spacing to get best possible estimate (find total torque of dominoes, conclude torque of ramp) ... center of mass of Earth-Moon system
introduce tan accel vector?
questions based on qa's completed
At what angular velocity would the domino slide off the strap if positioned at 10 cm from the axis of rotation, assuming coefficient of static friction mu_static = .3?
`q002. Earth's mass is about 6 * 10^24 kg. The Moon's mass is about 1/60 times the mass of the Earth. The two are separated by about 370 000 km.
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
****
&&&&
`q003. What is the velocity of a satellite in a low-Earth orbit at a distance of 7000 km from the center of the Earth?
What are the KE and PE of this orbit?
If a satellite changes from a circular orbit at 7000 km from the center of the Earth, to a circular orbit at 7001 km, what is `dKE between the orbits and what is `dPE?
How much work must have therefore be done on the system by nonconservative forces?
`q004. The Moon's orbit around the Earth is actually elliptical, with its closest approach occurring around 360 000 km and its furthest distance around 380 000 km.
No significant nonconservative forces act on the Moon in its orbit.
Does the Moon gain or lose KE as it moves from the 380 000 km distance to the 360 000 km distance? How much KE does it gain or lose? (hint: you should start by calculating the Moon's PE at both points; you should not start by assuming that the Moon moves between two circular orbits with radii 380 000 km and 360 000 km)
`q005. An object moves around a circle with radius r = 100 cm at velocity v = 50 cm/s and centripetal acceleration a_cent = 25 cm/s^2.
Sketch the radial, velocity and centripetal acceleration vectors corresponding to angular position theta = 45 degrees. Sketch the x component of the radial vector.
Sketch auxiliary axes to determine the directions of the velocity and centripetal acceleration vectors, and using the auxiliary axes sketch the x components of each of these vectors.
Describe your sketch in detail:
^^^^
&&&&
Estimate the x component of each vector. Give your estimates below.
^^^^
&&&&
Using sines and/or cosines as appropriate, calculate the x component of each vector.
Give your calculations below
^^^^
&&&&
Repeat for angles theta = 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
List the x components of the radial vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
&&&&
List the x components of the velocity vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
&&&&
List the x components of the centripetal acceleration vector for angles 45 deg, 90 deg, 135 deg, 180 deg, 225 deg, 270 deg, 315 deg and 360 deg.
^^^^
&&&&
Can the x component of the position vector have the same sign as the x component of the velocity vector?
^^^^
&&&&
Can the x component of the position vector have the same sign as the x component of the centripetal acceleration vector?
^^^^
&&&&
Can the x component of the centripetal acceleration vector have the same sign as the x component of the velocity vector?
^^^^
&&&&
Geosychronous satellite
A geosychronous satellite orbits the Earth once per day. The period of the orbit is therefore 24 hours.
We want to find the radius r of this orbit.
Recall that by setting centripetal force equal to gravitational force we find the velocity of a circular orbit of radius r is
The velocity of an orbit is also v = `ds / `dt, where `ds is the distance around the orbit and `dt the time requires to complete an orbit. The circumference of the orbit is 2 pi r so
We therefore have two equations in the unknowns v and r. We can easily solve the equations simultaneously to determine r. Setting our two expressions for v equal, we eliminate v and obtain the equation
which we easily solve for r, obtaining
`q006. What are the radius and velocity of a geosychronous orbit?
^^^^
&&&&
Don't do the calculation, but explain how you would use your information to calculate the total mechanical energy (total mechanical energy = PE + KE) of the orbit.
^^^^
&&&&
Getting used to negative PE
Let's assume that everyone in this discussion has the same mass.
If you are at the bottom of the well and I am at the opening to the well, you will easily come to the conclusion that my PE is greater than yours, since you would have to do work against gravity to get to my position.
You might choose to think that your PE is zero and that mine is positive.
I might choose to think that my PE, since I'm on the surface, is zero and yours is negative.
Either of us would be right, but without a common reference point we would come to very different conclusions about PE.
For example a guy halfway down the well would have negative PE according to my reference point, and positive according to yours. We might agree on how much PE he would lose if he fell to your position, or how much he would gain if he climbed up to mine, but if we want to describe his PE in terms of a single number, we won't be able to do it.
Suppose we agree to use my perspective: PE is zero at the surface of the Earth.
Then the guy halfway down has negative PE, and you have even more negative PE. Both PE's are negative, but yours has the greater magnitude. At the same time your PE is less than his; since your negative number has greater magnitude, it's further 'below zero' than his, so it's less.
Just as we agreed to use the surface of the Earth as the reference point for the example of the well, we need to agree on a reference point for orbital PE. In this case our reference point is 'far, far away'. In fact it's the limit of 'far, far away', an infinite distance.
If we agree to measure PE relative to infinity, then we use the formula PE = - G M m / r. This formula takes care of the fact that g keeps changing (which makes m g h irrelevant since you don't know what value to use for g).
Using this formula everything has negative potential energy. The smaller the value of r, the greater the magnitude of the PE, so things closer to the center of the Earth have a negative PE which less than (but of greater magnitude than) the PE they would have if they were further.
This is analogous to the example of the well. If you're on the surface of the Earth you now have a big negative PE; if you're in orbit halfway to the Moon you have a negative PE but not as big as the one you had on the surface; and to go from a bigger negative PE to a smaller negative PE, your PE has to increase. Put another way, your PE at the surface is 'way below zero'; halfway to the Moon it's still below zero, but not as far below, and to get there your PE must increase.
Homework:
Your label for this assignment:
ic_class_091118
Copy and paste this label into the form.
Answer the questions posed above.
You have already seen most of the ideas in the qa's and Introductory Problem Set mentioned below. If you work through these documents as assigned, you will get plenty of practice and should develop good expertise with these concepts.
Do qa's #34 on moments of inertia and 35 on SHM.
Introductory Problem Set 9 consists of 17 problems on simple harmonic motion. You will be expected to work through these problems by the first of next week. http://vhmthphy.vhcc.edu/ph1introsets/default.htm .
upcoming:
pick up for further expertise
still to be assigned:
`q003. What is your gravitational PE, relative to infinity, at the surface of the Earth? How much KE would you therefore need to make it to infinity? Over what minimum distance would you have to be accelerated in order to survive?
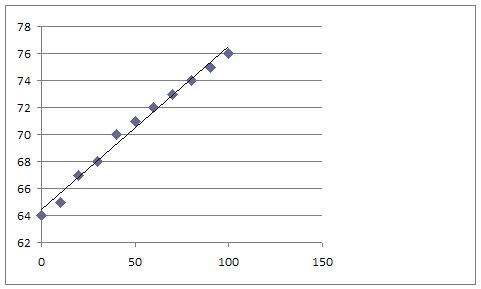
Excel note: If you right-click on the straight line, then on Format Trendline, then on Options and check the box Display Equation on Chart, you will see the actual best-fit equation. In this case the equation is y = 0.1209x + 64.409. Note that the equation I used above was based on an eyeball estimate of the coordinate of the x = 25 and x = 75 points, and I got a slope of .135 rather than .121. For an eyeball estimate this isn't bad. However had I used a printout and drawn straight projection lines, and had I accurately located x = 25 and x = 75, the estimate would likely have been more accurate.
| Relative Humidity (%), x | Apparent Temperature F, y | ||||
| 0 | 64 | ||||
| 10 | 65 | ||||
| 20 | 67 | ||||
| 30 | 68 | ||||
| 40 | 70 | ||||
| 50 | 71 | ||||
| 60 | 72 | ||||
| 70 | 73 | ||||
| 80 | 74 | ||||
| 90 | 75 | ||||
| 100 | 76 | ||||