Class Notes 100915

Existing QA Documents

Here is a listing of qa documents.  Don't try to digest them all at once.  Give yourself until at least Monday.  (just kidding)

Seriously, these are question-answer introductions to the main topics in first-semester physics.  If you are having trouble with the questions I've been posting, the qa's can help.  At this point I recommend QA's numbered 2-13; number 7 could be skipped for right now, but will soon become relevant.  You can read the questions and answers, you can submit the documents or parts of the documents with attempts at solutions, questions, self-critiques, you can not to use them at all because you already understand their content (or because other activities work better for you).

If you do choose to submit the qa's, as I do recommend if you haven't been submitting work, don't think in terms of doing them all at once.  Take them one at a time, but do put in the necessary time.

• ../ph1_qa_2.htm on Velocity
• ../ph1_qa_3.htm on Velocity Relationships
• ../ph1_qa_4.htm on Acceleration
• ../ph1_qa_5.htm on Uniformly Accelerated Motion
• ../ph1_qa_6.htm on using the equations of Uniformly Accelerated Motion.
• ../ph1_qa_7.htm on the Acceleration of Gravity.
• ../ph1_qa_8.htm on Using the Acceleration of Gravity; summarizing the analysis of uniformly accelerated motion
• ../ph1_qa_9.htm on Forces exerted by gravity; nature of force; units of force
• ../ph1_qa_10.htm on Force and Acceleration
• ../ph1_qa_11.htm on situations involving force and acceleration
• ../ph1_qa_12.htm on Problems involving Motion and Force
• ../ph1_qa_13.htm on Energy
• ../ph1_qa_14.htm on Potential energy; conservative and non-conservative forces
• ../ph1_qa_15.htm on Impulse-Momentum
• ../ph1_qa_16.htm on Projectiles
• ../ph1_qa_17.htm on Collisions
• ../ph1_qa_18.htm on Vectors
• ../ph1_qa_19.htm on Vector Quantities
• ../ph1_qa_20.htm on Forces (inclines, friction)
• ../ph1_qa_21.htm on Projectiles (part 2)
• ../ph1_qa_22.htm on Motion in a Force Field
• ../ph1_qa_23.htm on Forces (Atwood machine, chains)
• ../ph1_qa_24.htm on Centripetal Acceleration
• ../ph1_qa_25.htm More Forces
• ../ph1_qa_26.htm More Forces (buoyant forces)
• ../ph1_qa_27.htm on Newton's Law of Universal Gravitation
• ../ph1_qa_28.htm on Orbital Dynamics
• ../ph1_qa_29.htm on Radian measure of angle; angular position, angular velocity
• ../ph1_qa_30.htm on Rotational Motion
• ../ph1_qa_31.htm on Torques and their Effect on Radian Motion
• ../ph1_qa_32.htm on Moment of Inertia
• ../ph1_qa_33.htm on Rotational KE and angular momentum
• ../ph1_qa_34.htm on Simple Harmonic Motion
• ../ph1_qa_35.htm on Velocity and Energy in Simple Harmonic Motion

Lab grade

Remember that you must perform the lab activities (as everyone is doing) and submit your work (so far this is done by answering the questions I pose for the labs).  A passing lab average is a prerequisite for a passing grade in the course.

Right now our goal is to become familiar with the basic systems studied in this course, and your lab grade at this point is determined by the effort you put into the process as well as the quality of your data and your analysis, and your overall responses.  Everyone who makes the required effort, submitting all requested lab work with at least adequate quality, can expect to have an A for their lab grade at this point of the course, and will build a solid foundation for later lab work.  Exceptional quality will, of course, be rewarded throughout the term.

Inserting answers

You have been inserting your answers in the lines between the ends of the questions and the #$&* mark.  Starting with this assignment, you will see **** in the line immediately following each question, and #$&* below that.  Please insert your answers starting on a new line between the **** and #$&*.  The **** and #$&* should each be alone on its own line, one before and one after your response.   If you have already inserted your answers into a document lacking the ****, that's OK. 

Experiments

Note:  numbers as opposed to quantities:

• Often a question will ask you to list numbers.  When asked for numbers you should give only the numbers, without the units and without any words of description.  Of course the units and descriptions are important., so after listing the numbers for all your data you will then be expected to state the units and the meaning of your numbers in a subsequent line.
• If a question asks for quantities, then the units should be included.  A brief explanation of meaning is generally expected after you complete your listing of quantities.

For the toy car and magnets:

Give the three positions you measured for each trial, one trial to each line.  Each line should consists of three numbers, representing the position in cm of the fixed magnet, the position in cm of the magnet of the toy car, and the position in cm at which the car came to rest after being released.  This is your raw data: 

****

#$&*

Give a brief explanation of what the data mean, including a statement of the units of the numbers:

****

#$&*

For each trial, give the distance of separation between the two magnets at the instant of release, and the distance the car traveled between release and coming to rest.  Give in the form of two numbers to a line, separated by commas, with separation first and coasting distance second.  After the last line, give a brief explanation of how your results were obtained and what the numbers mean, including a statement of the units of the numbers.

****

#$&*

Sketch a graph of distance traveled vs. initial separation.  Describe your graph.

****

#$&*

Sketch the smooth curve you think best represents the actual behavior of distance traveled vs. initial separation for this system.

****

#$&*

Identify the point where initial separation is 8 cm. 

• What coasting distance corresponds to this point? 
• What is the slope of your smooth curve in the neighborhood of this point? 

Give the coasting distance as a number in the first line, the slope of the graph as a number in the second line.  Starting in the third line give the units of your quantities and explain what each quantity means, and how you obtained it.

****

#$&*

Repeat for the point where initial separation is 5 cm.

****

#$&*

According to your graph, if the initial separation is doubled, what happens to the distance the car travels?

****

#$&*

According to your graph, if the initial separation is doubled, what happens to the slope of the graph?

****

#$&*

The distance the car travels is an indication of the energy it gained from the proximity of the magnets.  Specifically, the frictional force slowing the car typically is about .01 Newton, or 10 milliNewtons.  The force exerted on the car by friction is in the direction opposite the car's displacement, so when you calculate the work done by this force, your force and the displacement will have opposite signs (i.e., one will be positive and the other will be negative).

Using the .01 Newton = 10 milliNewton force and your displacement in meters (you likely calculated the displacement in centimeters, so be sure you use the equivalent displacement in meters) find the work done by this force on each of your trials.  Give below the initial separation of the magnets, the work done by the frictional force acting on the car in Newtons * m, the work in milliNewtons * m, in the form of three numbers per line separated by commas.  In the first subsequent line, explain your results and include a detailed sample calculation.

Friction does negative work on the coasting car, which progressively depletes its kinetic energy (recall that kinetic energy is energy of motion).  In this situation the original kinetic energy of the car came from the configuration of the magnets (the closer the magnets, the greater the KE gained by the car).  We say that the initial magnet configuration had potential energy, with closer magnets associated with more potential energy.  The initial potential energy of the magnets was therefore converted into the initial kinetic energy of the car, which was then lost to friction as friction did work on the car equal and opposite to its initial kinetic energy.  (actually the potential-to-kinetic-energy transition takes place over a significant interval of time and distance, so it would be more appropriate to speak of the work by friction on the car begin equal and opposite to the initial potential energy, but we won't really worry much about that just yet). 

Explain this below in your own words, as best you understand it.

#$&*

The car also exerts a frictional force on the table which is equal and opposite the frictional force exerted on it (if the table was on frictionless rollers the frictional force exerted by the car would cause the table to accelerated very slowly in the direction of the car's motion), so it does work against friction which is equal and opposite to the work friction does on it.  So the car does positive work against friction.  This work is done at the expense of its kinetic energy.

If you were to make a table showing work done by the car against friction vs. initial separation it would be the same as the table you gave previously, except that the work would be positive (you did remember to make the work negative on the previous table, didn't you?).  I'm not going to ask you to give that table here, since except for the sign of the work it is the same as your previous table.

What we are going to want is a graph of the work done by the car against friction, vs. initial separation.

You already have a graph of distance vs. initial separation. 

You can add a new labeling to your vertical scale to represent the corresponding work done by the car against the frictional force. 

If you don't understand what this means, you can go ahead and create a separate graph of work done vs. initial separation. 

Either way:

According to your new graph, or the new labeling of your original graph, what is the work done by the car against friction when the initial separation is 8 cm?  Give the quantity in the first line, a brief explanation in the second.

****

#$&*

Repeat for initial separation 5 cm.

****

#$&*

According to your graph, how much more work was done against friction when the initial separation was 5 cm, than was done when initial separation was 8 cm?

****

#$&*

How much work was therefore done by the magnetic force between the 5 cm and 8 cm separation, while the cars were moving apart?

****

#$&*

For a system released at a separation of 5 cm or less, the magnets exerted a decreasing force between the 5 cm separation and the 8 cm separation.  The force has an average somewhere between the forces exerted at the 5 cm and 8 cm separations.  If you answered the preceding question correctly you know the work between the two positions.

Through what displacement did the magnetic force act between these two separations?

How can you calculate the average force given the displacement and the work?

What therefore was the average force?

****

#$&*

What therefore is the average rate at which work is being done by the magnets, per unit of separation, between the 5 cm and 8 cm separations? 

What aspect of the graph of work vs. separation is associated with this average rate?

****

#$&*

What is your best estimate of the average rate at which work is being done by the magnets, per unit of separation, when the magnets are 6 cm apart?

****

#$&*

In general how can you use a graph of work vs. separation to this system to find the force exerted by the magnets at a given separation?

For the car and paperclips

Let 1 unit of force correspond to the weight of 1 small paperclip.  On this scale the weight of a large paperclip is 3 units of force.

If the paperclip is on the car, its weight is balanced by the upward force exerted by the table and it has no direct effect on the car's acceleration.  If it is suspended, then its weight contributes to the accelerating force.

You should have obtained a count and a distance from rest for each trial, and on each trial there will be some number of force units suspended from the thread (1 unit for every small, 3 units for every large clip).  Report in the first line the number of clips, the count and the distance from rest, separated by commas, for your first trial.  Report subsequent trials in susequent lines.  After reporting the data for all your trials, give a brief explanation of your setup and how the trials were conducted.  Include also the information about how many of your counts take how many seconds.

****

#$&*

Determine the acceleration for each trial.  You may use the 'count' as your unit of time, or if you prefer you can convert your counts to seconds and use seconds as your time unit.  In each line below list the number of suspended force units and your acceleration.  After reporting your results, give in the next line the units and your explanation of how your results were obtained.

****

#$&*

Sketch a graph of acceleration vs. number of force units, and describe your graph.  Fit a straight line to your graph and determine its slope.  Describe how the trend of your data either indicates a good straight-line fit, or how it deviates from a straight line.

****

#$&*

Brief at-home experiment

Is the magnitude of a ball's acceleration up an incline the same as the magnitude of its acceleration down the incline?

Test this.

One possible suggested method:  Use the short ramp to get the ball started, and let it roll from the short ramp onto the longer ramp, with the longer ramp inclined so the ball rolls up, rather than down.  Get the ball started on the short ramp, either by inclining it toward the long ramp or giving it a push (before it reaches the long ramp).  Click the TIMER at the instant the ball hits the 'bump' between the two ramps, again when the ball comes to rest for an instant before accelerating back down the long ramp, and once more when the ball again hits the 'bump'.

Everyone will tend to anticipate their 'clicks', and to try to compensate for their anticipation.  If the effect of anticipation is the same for all three timed events, then uncertainties in your results will all be due to the TIMER.  If the degree of anticipation differs, as it inevitably will, then the uncertainties are compounded.  If the degree of anticipation (and/or compensation) tends to be either greater or less for the second event (the ball stopping for an instant) than for the first and third (the 'clicks' made when the ball hits the 'bump'), then a systematic error is introduced (you will have a tendency to 'short' one interval while extending the other).  

If there exists a difference between the times up and down the ramp, and if the difference is great enough to show through the uncertainties and systematic errors, then you might get a useful result (e.g., either the actual times are the same, or they differ).

Give a brief report of your data and your results:

****

#$&*

Displacement and force vector for a rubber band

The points (2, 1) and (4, 6) have the following characteristics:

• From the first point to the second the 'run' is 4 - 2 = 2 and the 'rise' is 6 - 1 = 5.
• The slope of the line segment connecting the points is therefore 5 / 2 = 2.5. 
• A right triangle can be constructed whose hypotenuse is the line segment from (2, 1) to (4, 6), and whose legs are parallel to the coordinate axes.  The leg parallel to the x axis has length 2, and the leg parallel to the y axis has length 5.  The hypotenuse therefore has length sqrt(2^2 + 5^2) = sqrt(29) = 5.4, approx..
• The area of the trapezoid formed by projecting the two points onto the x axis, whose sides are the projection lines, the segment [2, 4] of the x axis and the line segment between the two points, has 'graph altitudes' 1 and 5, giving it average 'graph altitude' (1 + 6) / 2 = 3.5, and width 5 - 1 = 4, so its area is 14.
• The vector from the first point to the second has x component 2 and y component 5.  Its length is sqrt(20) and its direction is specified by the ratio of the y to the x component.

Any time you see two points on a graph you should be aware that you can easily construct the right triangle and use it to calculate the slope of the segment joining them, the distance between the points, the area of the associated trapezoid and the components of the vector.  Depending on the nature of the graph, some of these quantities will sense and be have useful interpretations, while others probably will not.

In the particular example of a rubber band stretched between the two points, with the coordinates in centimeters, the most important quantities are the components and length of the vector.  The vector from the first point to the second is in this case a displacement vector.  The displacement vector has x component 2 cm, y component 5 cm and length sqrt( 2 cm)^2 + (5 cm)^2 ) = sqrt( 29 cm^2) = sqrt(29) cm, about 5.4 cm. 

• We denote the displacement vector from (2 cm, 1 cm) to (4 cm, 6 cm) as  <2 cm, 5 cm>

If we divide the this vector 2 we get a vector of length 2.15 cm.  The x component will be 1 cm (half of the original 2 cm) and the y component 5 cm /2 = 2.5 cm (half of the original 5 cm).  The ratio of the components is the same, so this vector will be in the same direction as the original vector.  If we multiply this vector by 2 we get a vector of length 8.6 cm.  Its components will be double those of the original vector, and it will also be in the same direction as the original vector.

If we divide our vector by 5.4 cm, then the resulting vector has length 5.3 cm / (5.3 cm) = 1.  The x and y components will be 2 cm / (5.4 cm) = .37 and 5 cm / (5.4 cm) = .92.  As before, the ratio of the components is the same as for the original vector (accurate to 2 significant figures),

The vector <.37, .92> has magnitude 1 (calculated to 2 significant figure), as you can easily verify using the Pythagorean Theorem.  Its direction is the same as that of the displacement vector <2 cm, 5 cm>.

Now we invoke a rule to find the tension in the rubber band.  Assume that for this rubber band the tension is .5 Newtons for each centimeter in excess of its 'barely-exerting-force' length of 4.8 cm. 

• The 5.4 cm length of the stretched rubber band is therefore .6 cm in excess of the 'barely-exerting-force' length of 4.8 cm.
• According to the rule, we conclude that the tension is therefore .6 cm * .5 N / cm = .3 N.

The vector <.37, .92> has magnitude 1, and its direction is the same as that of the displacement vector.  A rubber band can exert a force only in the direction of its displacement vector. 

• If we multiply our vector <.37, .92> , which we again mention has length 1, by .3 N, we will obtain a vector whose magnitude is .3 N.  (whatever quantity we multiply by a vector of length 1, we end up with a vector whose length is equal to that quantity, or more correctly whose length represents that quantity)
• The direction of this vector will be the same as that of our original vector.
• <.37, .92> * .3 N = <0.11 N, 0.28 N>
• This is the tension vector.  It tells us that the tension of this rubber band has x component 0.11 N and y component 0.28 N. 

Using your data from the rubber band experiment, check your previous calculations of the displacement vector, the unit vector and the force vector for each rubber band.  If your original work on this experiment was not done correctly, please correct it and resubmit.  Please acknowledge that you have read this instruction and understand it.

****

#$&*

Linear force function and work\energy

If the graph below indicates the tension in Newtons vs. length in cm for a rubber band:

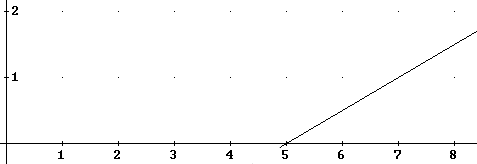
At what length does the rubber band begin exerting a force?

****

#$&*

What is the average force exerted between the lengths x = 5 cm and x = 7 cm?

****

#$&*

As the rubber band is stretched from length 5 cm to length 7 cm, through what distance is the force exerted?

****

#$&*

How much work is therefore done in stretching the rubber band from 5 cm to 7 cm length?

****

#$&*

How much work is done in stretching the rubber band from the 5 cm length to the 8 cm length?

****

#$&*

How much work is done in stretching the rubber band from the 6 cm length to the 8 cm length?

****

#$&*

What are the areas beneath the graph between each of the following pairs of lengths:

• x = 5 cm and x = 7 cm
• x = 5 cm and x = 8 cm
• x = 6 cm and x = 8 cm
• x = 7 cm and x = 8 cm

****

#$&*

Verify that the equation of the straight line in the given graph is F(x) = (x - 5) * .5, where F(x) is force in Newtons when  x is position in centimeters.

****

#$&*

University Physics Students:  Confirm your results for graph areas by integrating the force function over appropriate intervals.  Suggested method:  Integrate the function symbolically from x = a to x = b, then use the resulting expression for appropriate values of a and b.

****

#$&*

Nonlinear force function and work\energy

The graph given previously was linear.  That graph would be realistic for a well-made spring, but not for a rubber band.

The graph given below is more realistic.

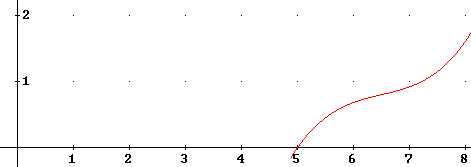
Estimate the average force exerted by this rubber band between the x = 5 cm and x = 6 cm lengths.  Give your estimate in the first line, and explain how you made the estimate in the second:

****

#$&*

Repeat, for the x = 6 cm to x = 7 cm length interval.

****

#$&*

Repeat, for the x = 5 cm to x = 5.5 cm length interval.

****

#$&*

Repeat, for the x = 5.5 cm to x = 6 cm length interval.

****

#$&*

Estimate the work done in stretching the rubber band for each of these intervals.  Give your four estimates in the first line below, separated by commas.  Starting in the second line explain how you got your estimates:

****

#$&*

How much work do you estimate is done between the x = 5 cm length and the x = 7 cm length?  Give your estimate in the first line, your explanation starting in the second.

****

#$&*

If a trapezoid was constructed by projecting the x = 5 and x = 7 points of the graph, what would be its area, and would this result be an overestimate or an underestimate of the actual area beneath the graph between these two points?

****

#$&*

If a trapezoid was constructed by projecting the x = 5 and x = 8 points of the graph, what would be its area, and would this result be an overestimate or an underestimate of the actual area beneath the graph between these two points?

****

#$&*

University Physics Students Only:

Note that these questions are easy to answer, if you understand what to do.  Understanding what to do is fairly challenging at this point.  I expect that some will get this, and some will not, and I can't predict who will fall into which category.  Of course I'd love it if you would make it easy on me, and everyone would get these:

Suppose the function for the tension is T(L) = (L-6.5)^3*.15 + .5 + (L-5)*.2.  How much work is done between length L = 5 cm and L = 7 cm, according to this function?

****

#$&*

How much work is done between lengths L = L_1 and L = L_2?  Apply your expression to the work done over each of the following intervals:

• L = 5 cm to L = 6 cm
• L = 6 cm to L = 7 cm
• L = 5.5 cm to L = 6 cm
• L = 5.5 cm to L = 7 cm

Give your four results in the first line below, separated by commas.  Starting in the second line explain how you got your results.

Directions of force and displacement vectors matter for work\energy

If force F and displacement `ds are both along the x axis, then what is the sign of F * `ds in each of the following cases:

• F is in the positive direction and `ds is in the positive direction.
• F is in the positive direction and `ds is in the negative direction.
• F is in the negative direction and `ds is in the positive direction.
• F is in the negative direction and `ds is in the negative direction.

Give your answers in the given order, in the first line below, separated by commas.  Starting in the second line explain how you got your results.

****

#$&*

If the x axis in the car-and-magnet experiment was your meter stick, then what were the directions of F and `dx, in each of the following situations:

• F is the force exerted on the 'car magnet' by the 'fixed magnet', `dx is the displacement of the car for 10 cm after its release.
• F is the force exerted on the 'car magnet' by the 'fixed magnet', `dx is the displacement of the car as you move it toward the last 10 cm toward the 'fixed magnet'.
• F is the force exerted by the 'car magnet' on the 'fixed magnet', `dx is the displacement of the car for 10 cm after its release.
• F is the force exerted by the 'car magnet' by the 'fixed magnet', `dx is the displacement of the car as you move it toward the last 10 cm toward the 'fixed magnet'.
• F is the force exerted on the car by friction, `dx is the displacement of the car after being released.
• F is the force exerted by the car against friction, `dx is the displacement of the car after being released.

Give your six answers in the first line below, separated by commas.  Starting in the second line explain how you reasoned out your answers.

****

#$&*

The figure below represents two plausible force vs. separation models for two of the ceramic magnets used in the experiment.  Force is in Newtons while separation is in centimeters.

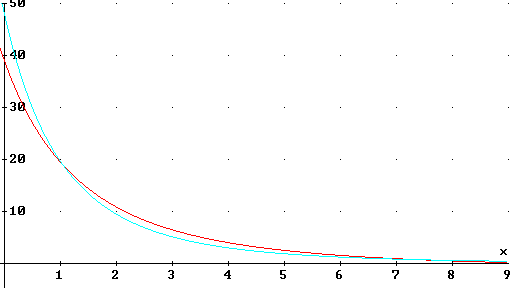
If the two magnets were touching before release, which model appears to predict the greater kinetic energy at the x = 2 cm position, and which at the x = 9 cm position?

****

#$&*