Notes from Class 101006

Oscillating_balance

Forces_on_a_suspended_object;_Atwood_Machine

Analyzing Graphs of Magnet_system_(University_Physics_only)

Ball off ramp to floor:  calculating v0 (University Physics only)

Oscillating balance

The volume of a rectangular solid or a cylinder with uniform cross-sectional area A_cs and length L is the product of its length and cross-sectional area.

The same applies to any object with constant cross-sectional area.

An object suspended in the water of the buoyant balance displaces a volume of water equal to the volume of that part of the object which lies below the surface of the water.

The buoyant force on the object is in the direction opposite the gravitational force, and is equal to the weight of the displaced water.  (We will see later why this is so; for now simply accept that Archimedes' Principle works).

`q001.  Explain the forces involved in the oscillation of the balance, as it moves through a complete cycle.

****

#$&*

Forces on a suspended object; Atwood Machine

The figure below depicts a ball in three situations.  In each situation exactly two forces act on the ball.  The forces are represented by vectors.

`q002.  In which situation is the ball accelerating toward the top of the page, in which situation is it accelerating toward the bottom, and in which would its acceleration most plausibly be zero?

****

#$&*

`q003.  If the downward arrow in each figure represents the force exerted by gravity, estimate the acceleration of each ball.  Specify the direction you choose as positive, and give the acceleration of each as a positive number, a negative number or zero.

****

#$&*

`q004.  The downward vectors in the figure below represent the forces of gravity on two different objects, while the upward vectors represent the tensions in strings supporting the objects.

• Which object has the greater mass?
• At the accelerations of the objects in the same direction, or in opposite directions?
• For which object do you think the magnitude of the acceleration is greater?

****

#$&*

`q006.  Based on a gravitational acceleration of 10 m/s^2, estimate the acceleration of each of the objects in the preceding figure. 

Is it plausible that the forces on the two objects depicted in the figure represent the forces acting on two objects, if they are connected by a string and suspended from opposite sides of a low-friction pulley?

****

#$&*

`q007.  For the figure below, let T stand for the upward force and m g for the downward force.  T is a vector, as is g.  The magnitudes of these vectors are T and g.

Both vectors act along a common axis, so they can be represented by positive and/or negative numbers. 

• If upward is chosen as the positive direction, then would we say that T = T or that T = - T?
• If upward is chosen as the positive direction, then would we say that g = g or that g = - g?
• If downward is chosen as the positive direction, then would we say that T = T or that T = - T?
• If downward is chosen as the positive direction, then would we say that g = g or that g = - g?

****

#$&*

`q008.  The net force acting on the object is T +  g.  Specify which direction you wish to declare as the positive direction, and in terms of T, m and g write the expression for the net force acting on the above object.  Your expression could be one of the following:  T + mg, T - mg, -T + mg, -T - mg.

****

#$&*

`q009.  If we know that the object in the above has acceleration a, then what does Newton's Second Law tell us about the net force on it?

****

#$&*

`q010.  You should now have two expressions for the net force, one in terms of T, m and g and the other in terms of m and a.  Set the two expressions equal to obtain an equation relating the quantities T, m, g and a.  What is your equation?

****

#$&*

`q009.  Solve your equation for T in terms of m, g and a.  Show your steps and briefly explain each.

****

#$&*

`q011.  In the figure below the two objects are shown with their gravitational force vectors, with an equal and opposite tension vector supporting each.  As depicted, each experiences net force zero and hence acceleration zero.

The figure also contains two equal and opposite 'unattached' vectors to the right of the two objects.

If one of the unattached vectors is added to the tension vector of one object, and the other to the tension vector of the other, then one object will have a net upward force and the other a net downward force. 

• Will the resulting accelerations be equal and opposite?

****

#$&*

`q012.  Sketch the above figure, but with the tension vectors modified so that the two objects will have equal and opposite accelerations.  Describe as precisely as you can how you would modify the figure.

****

#$&*

If the two objects suspended over a pulley have respective masses 1.4 kg and 1.0 kg, then a force diagram for the entire two-mass system is easily sketched.  The figure below depicts the situation as it would be if the tension forces were sufficient to just hold the system in equlibrium:

However if the pulley has negligible mass and friction, the tension in the string is constant, so the two tension vectors must be equal and opposite.  This means that the tension on the right must increase, and the tension on the left must decrease.

`q013.  Answer the following questions:

• If the tension on the right increases, will the net force on the mass at right be upward or downward?   
• If the tension on the left decreases, will the net force on the mass at left be upward or downward?  
• What therefore will be the directions of acceleration of the two masses?
• Is your response consistent with the observed behavior of such a system?

****

#$&*

To figure out the tension in the string, we analyze the system as a whole:

• Gravity exerts a force of about 10 N on the mass at right, and a force of about 14 Newtons on the mass at left.
• The two masses form a system with a constant acceleration.  The accelerations of the individual masses have opposite signs, but when regarded as a single system the acceleration must have a single sign.  This means we have to choose a positive direction for the system in which one mass rises while the other falls.
• We can describe our chosen direction as 'clockwise' or 'counterclockwise', according to the direction of the pulley's motion.  This system is in fact to be regarded as a rotational system, rather than a linear system.  (The standard positive direction for rotational motion is counterclockwise, and this will be important later, but at this point you could choose either clockwise or counterclockwise as the positive direction).

If we choose counterclockwise as the positive direction, then our 14 N force tends to accelerate the system in the positive direction, the 10 N force in the negative direction.

• We conclude that the net force on the system is 14 N - 10 N = 4 N.

We can now use Newton's Second Law to find the acceleration:

• The mass of the system is 1.0 kg + 1.4 kg = 2.4 kg.
• The acceleration is therefore F_net / m = 4 N / (2.4 kg) = 1.7 m/s^2, approx..

We can now isolate and analyze the forces on each mass:

• We know the 1.4 kg mass accelerates downward at 1.7 m/s^2.  So the magnitude of the net force on it is F_net = m g = 1.4 kg * 1.7 m/s^2 = 2.2 N in the downward direction.
• Regarding downward as positive, the net force on this mass is T + m g, which must be equal to m a.
• Setting the two expressions for net force equal, we have T + m g = m a.  We know everything but T, so we solve to find that

T = m a - m g

= 1.4 kg * 1.7 m/s^2 - 1.4 kg * 10 m/s^2

= 2.2 N - 14 N = -11.8 N.

The tension in the string is therefore 11.8 N.

• We could apply the same reasoning to the 1.0 kg mass.  Again using downward as the positive direction, and noting that the acceleration is upward and hence negative:

m a = T + m g, with m = 1.0 kg, g = 10 m/s^2 and a = -1.7 m/s^2, so that

T = m a - m g

= 1.0 kg * (-1.7 m/s^2) - 1.0 kg * 10 m/s^2

= -1.7 N - 10 N = -11.7 N.

Downward was chosen as positive, so -11.7 N corresponds to an upward tension of 11.7 N.

• Our two tensions should be equal in magnitude.  Our results are therefore consistent, since calculations are within the +-1% limit expected  from two-significant-figure information.

Magnet system (University Physics only)

The coasting distance function y = 188 x^-1.083 has derivative about 200 x^-2.083, where y represents coasting distance in cm and x represents initial separation in cm. 

The associated PE function, assuming frictional force of magnitude 2000 dynes, is about PE(x) = 370 000 x^-1.083, where PE is potential energy in ergs when x is separation in centimeters.

The derivative of the coasting distance function is about d(PE)/dx = 400 000 x^-2.083.

The slopes you were previously asked to calculate for the associated graphs should match these values reasonably well.

The worksheet below shows calculations for the slope of the original graph at x = 4.3. 

• The estimated slope of the original graph was -9.5 cm / cm = -9.5, obtained by sketching the tangent line and estimating the points (0.8, 70) and (7.2, 10) on that line. 
• When the graph was rescaled to represent ergs vs. cm (accomplished by multiplying all y values by 2000 dynes), that slope became -19 000 ergs / cm = -19 000 dynes. 
• The rescaled derivative function was -420 000 x^-2.083 (obtained by multiplying the original derivative function y ' = -200 x^-2.083 by the same scaling factor as before).  Evaluating this function at x = -4.3 cm, we obtain a result very close to the -19 000 dynes estimate of the graph.

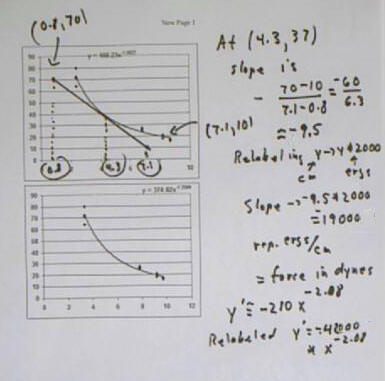
The next graph depicts the PE vs. separation. 

• The rescaling factor is closer to the 1800 dynes inferred from the original data than to the 2000 dynes used previously, so the function is closer to 340 000 x^-1.083 than to the previously used 370 000 x^-1.083.
• The x = 4.3 slope estimated above would be reduced by a similar factor, to about -17 000 ergs / cm.

The graph shown below corresponds to forces actually measured between the two magnets.  The uncertainty in measurements was not completely insignificant, but was less than +-5%.

`q014.  According to the graph shown above, what was the force at the 4.3 cm separation?

****

#$&*

`q015.  Estimate the area beneath the curve shown in the above graph, between x = 2 and x = 6.  Try to estimate the area with reasonable accuracy, say to within +- 10%.  A two-trapezoid approximation will get you close to this accuracy, then a commonsense adjustment should easily get you within 10%.

****

#$&*

`q016.  The function given in the force vs. separation graph is a simple power function and can be integrated very easily.

• What is an antiderivative of the function depicted in the force vs. separation graph? 
• By how much would this antiderivative change between x = 2 and x = 6? 
• What is the meaning of this result? 
• How is this related to previous result(s)?

****

#$&*

`q017.  To what degree are the two graphs consistent with one another?

****

#$&*

(note:  Based on a model in which the effects of the two magnets are modeled by a sheet of polarized particles at each flat surface, interacting with similar particles on the surfaces of the opposing magnet, we would not predict that a single power function can actually model the interactions.  You don't need to understand this model at this point of the course, but the conclusion is that we would not expect the two graphs to be completely consistent.)

Ball off ramp to floor:  calculating initial velocity of projectile

The general equations for projectile motion, as seen during the last class, are

• x = x0 + v0 cos(theta) * t and
• y = y0 + v0 sin(theta) * t - 1/2 g t^2

When we eliminate t from the equations (by solving the first for t and substituting the result into the second) we get

• v0 = +-sqrt( (g ( x - x0)^2 / (2 cos(theta)) / (y - y0 - ( (x - x0) sin(theta) / cos(theta) ) )

Simplifying we get

v0 = +- sqrt(2(x - x0) g)/(2·sqrt((cos(theta))·((y - y0)·cos(theta) - (x - x0)·cos(theta))) )

In standard notation the expression for v0 is