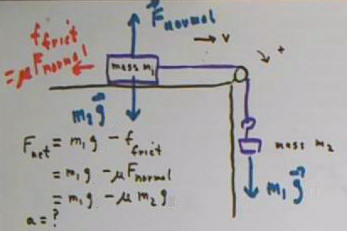
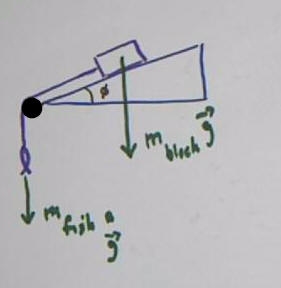
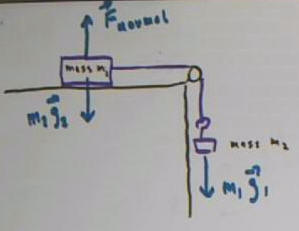
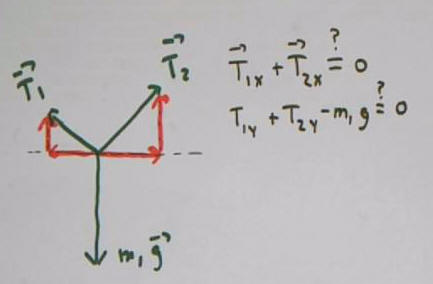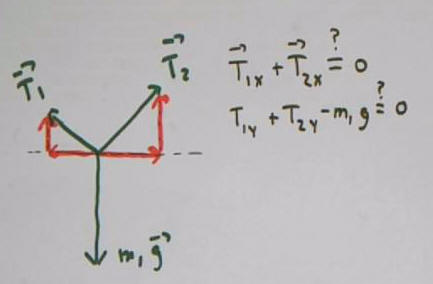The figure below depicts a block with mass m_block, on an incline with angle of elevation phi.  The mass attached by a light string over a pulley to a hanging fish of mass m_fish.

The weight vectors m_block g and m_fish g are depicted by vectors.

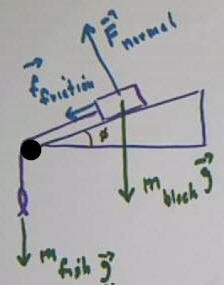
The incline exerts a force f_normal on the block, in a direction perpendicular to the incline.  There is also a frictional force f_friction between block and incline.  It isn't clear whether the block is moving, so it isn't clear in which direction to draw the vector for the frictional force.  We have chosen arbitrarily to sketch this vector acting down the incline.  If we later complete the analysis and the frictional force turns out to be up the incline, our analysis will give us a negative result, indicating that the vector should be in the direction opposite the indicated direction.

We begin our analysis.

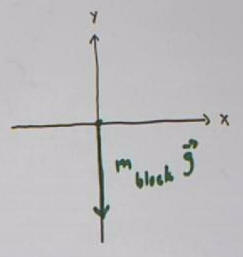
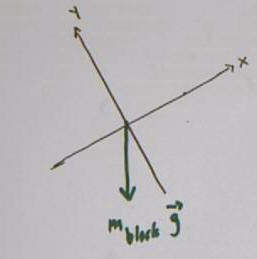
In the figure below the weight vector for the block is depicted on a coordinate system with the x axis horizontal and the y axis vertical:

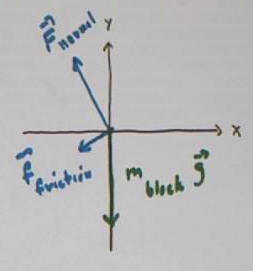
The forces F_normal and f_friction are added to the diagram so that all the forces acting on the block are represented:

The problem with this coordinate system is that the motion of the block along the incline will have both x and y components.  We avoid this complication by is rotating the coordinate system so that the x axis is directed along the incline.  Note that this requires a rotation of the system through angle phi, the original angle of elevation.

This orientation of the axes will also be convenient for determining the normal force, which is subsequently used in finding the frictional force.  The three forces are depicted on the rotated system:

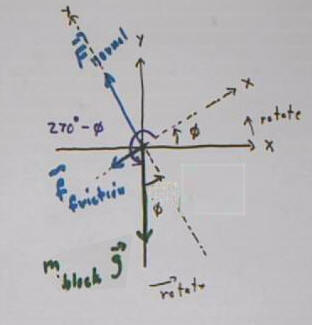
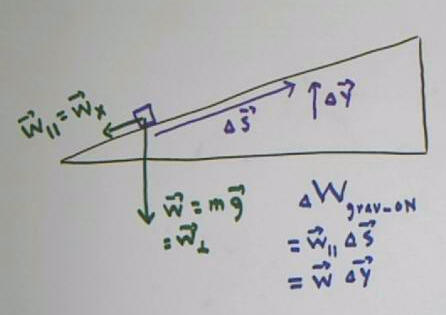
We further analyze the weight of the block:

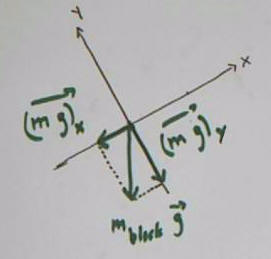
The weight vector is projected onto the x and y axes, giving us the x and y components (m g)_x and (m g)_y of the weight.

     

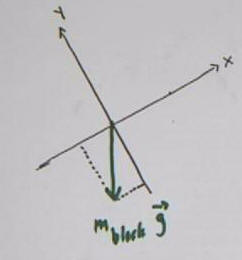
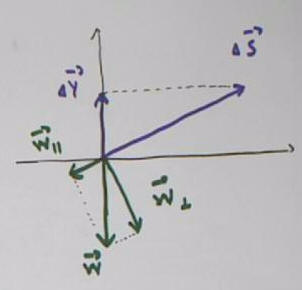
The gravitational, normal and frictional forces on the mass can be depicted as below:

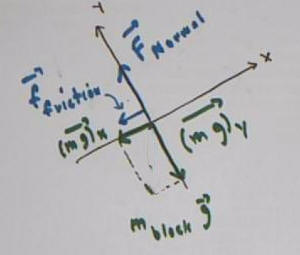
The block has zero acceleration, therefore zero net force, in the y direction, so the sum of the y forces F_normal and (m g)_y is zero.

The forces in the x direction are (m g)_x and f_friction.

If we return to the original situation, we can regard the fish and block as a system which accelerates at a single rate.  We can choose a positive direction for this system.  Given our coordinate system it would be natural to regard the 'clockwise' direction, in which the mass moves in the positive x direction and the fish ascends, and the positive direction.  It would also be natural (and more conventional) to regard the 'counterclockwise' direction as positive. 

Choosing the 'clockwise' direction, the net force on the system is

• F_net = -m_fish g - (m g)_x - f_friction

Five systems are depicted below.  Sketch each system and the corresponding force vectors.

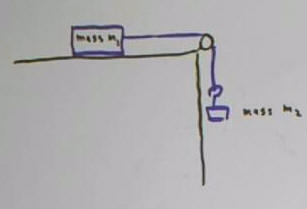
Mass m1 on a level surface, attached by a light string over a light frictionless pulley to suspended mass m2.

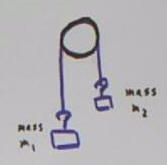
Masses m1 and m2 suspended by a light string over a light frictionless pulley.

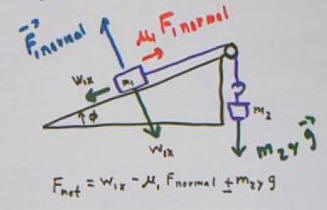
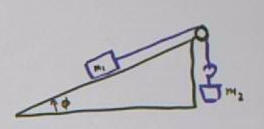
Mass m1 on incline with horizontal attached by light string over a light frictionless pulley to suspended mass m2.  Incline angle with horizontal is phi.

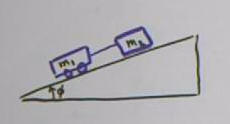
Mass m1 on frictionless wheels attached by light string to mass m2 sliding on incline.    Incline angle with horizontal is phi.

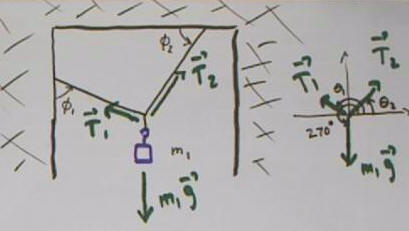
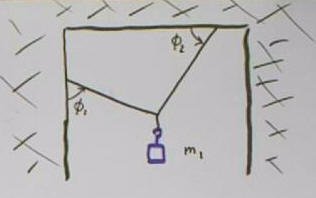
Mass m1 suspended by light strings from rigid wall and ceiling, first string at angle phi_1 with respect to left wall. second at angle phi_2 with respect to ceiling.

 

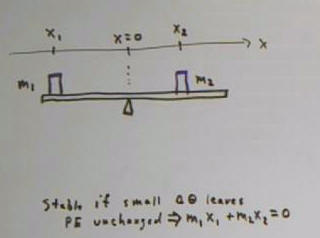
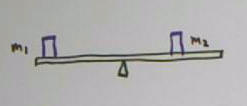
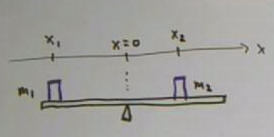
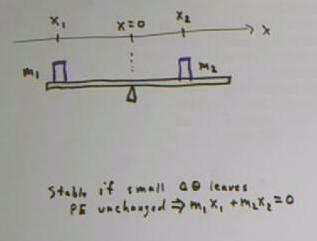
Masses m1 and m2 on light rigid beam balanced at fulcrum close to mass m2 than to mass m2.

  

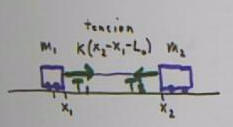
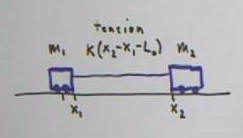
Masses m1 and m2 attached by a light elastic cord, with cord stretched.

The first of the above systems, with gravitational and forces.  Tension forces may be of interest, but are internal to the system have not been depicted at this point.  Frictional forces have not been included, so each sketch indicates the frictionless case.

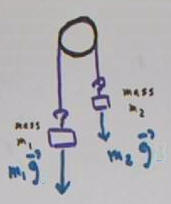
The Atwood system, with gravitational forces.  The pulley would also be supported by an upward force of m1 g1 + m2 g.

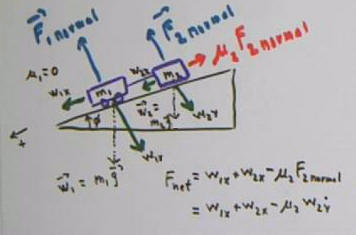
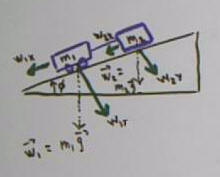
Two masses on incline, including weight vectors

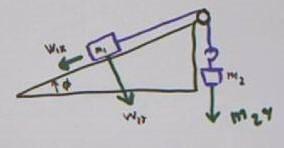
Mass on incline plus suspended mass, gravitational force on m1 broken into components w_1x and w_1y.  The weight is w = m g, and the components are w1_x = m g cos(theta) and w1_y = m g sin(theta), where theta is the angle of the weight vector with the positive x axis.

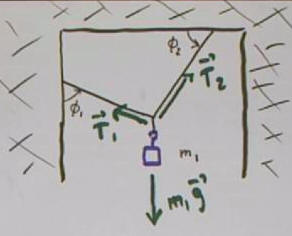
The forces on the mass suspended by three strings.  Each string exerts a tension force, tending to contract it.  The string supporting the mass also exerts a tension force which is not show, but is equal in magnitude to m1 g.

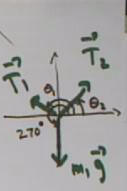
The three tensions can be depicted on a single set of coordinate axes, with the initial point of each vector at the origin.  The angles theta_1 and theta_2 of the tension vectors T1 and T2 are indicated.  You should be able to express each of these angles in terms of the given angles phi_1 and phi_2.

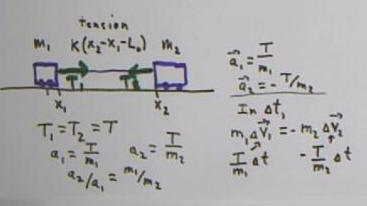
The tensions on the two masses connected by the stretched cord are equal and opposite.