The gravitational force on a mass sliding along an incline is m g , designated wt . 

• If the slope is small, then we can use the small-slope approximations for the magnitudes of the components:  wt_parallel = slope * wt and wt_perpendicular = wt
• wt_parallel is the component of the weight parallel to the incline, and constitutes the part of the gravitational force that tends to accelerate the mass. 
• wt_perpendicular is the component of the weight perpendicular to the incline, and if no other forces are present is equal in magnitude to the normal force.
• The frictional force is mu * F_normal, directed opposite the motion of the sliding mass.

In the present example, mu = .03 and slope = .05.

The parallel component is therefore .05 m g and the frictional force .03 mg.

• If the positive direction is up the ramp, then the parallel component is wt_parallel = -.05 m g.
• If motion is up the ramp, then the frictional force is f_frict = -.03 m g, directed opposite the motion.
• If motion is down the ramp, the frictional force is f_frict = +.03 m g, again directed opposite the motion.

For motion up the incline, then, we have

• F_net = -.05 m g - .03 m g = -.08 m g, and acceleration is a = F_net / m = -.08 m g / m = -.08 g.

For motion down the incline we have

• F_net = -.05 m g + .03 m g = .02 m g, and acceleration is a = F_net / m = -.02 m g / m = -.02 g.

.08 g is about 80 cm/s^2 and .02 g is about 20 cm/s^2. 

Our result corresponds to a fairly typical toy car, which has accelerations of magnitude 80 cm/s^2 when coasting up an incline, and 20 cm/s^2 when coasting down.

The 60 cm/s^2 difference is due to the frictional force, which acts alternately in the same direction as the parallel component of the weight, and opposite this direction.  The frictional force increases magnitude of acceleration by 30 cm/s^2 when motion is up the incline, and reduces it by 30 cm/s^2 when motion is down the incline.

• In this example, then, in the absence of friction the acceleration would have magnitude 50 cm/s^2, halfway between the observed 20 cm/s^2 and 80 cm/s^2 accelerations that result when friction is present.
• This 50 cm/s^2 acceleration would be the result of the parallel component of the weight, acting unopposed and unaided. 
• Had we known only that the accelerations when the object moves up and down the incline are 20 cm/s^2 and 80 cm/s^2 (both accelerations directed down the incline), we would have been able to conclude that the slope is .05.
• We would also have been able to conclude that friction is responsible for a 30 cm/s^2 increase in acceleration magnitude when the object is moving up, and a 30 cm/s^2 decrease when it is moving down the incline.  From this we would have concluded (again using small-slope approximations where normal force is of the same magnitude as the weight) that the coefficient of friction is about .03.

Reasoning similarly, if accelerations up and down are -.06 g and -.03 g, then the slope is .045 and mu is .015.

Check to see if you understand. 

If on another incline the acceleration of a ball rolling up the incline is 30 cm/s^2, and the acceleration when rolling down is 20 cm/s^2, then what are the slope of the incline and the coefficient of friction? 

Answer is given immediately below, but don't peek until you've figured it out, in detail.  See if you can figure out not only the right answers, but the complete reasoning process.

Answer:  Following the reasoning developed above, the effect of the incline itself is to accelerate the object at 25 cm/s^2, so the parallel component of the weight gives us an acceleration which is .025 as great as the acceleration of gravity.  Thus the parallel component is .025 of the weight, meaning that the slope is .025 (using the small-slope approximation)  Friction increases or decreases this by 5 cm/s^2, which is .005 times the acceleration of gravity, so the frictional force must be .005 times the weight.  In the small-slope approximation the magnitude of the normal force is equal to that of the weight, so the frictional force is .005 times the normal force, meaning that the coefficient of friction is mu = .005.

Some students expressed confusion with the idea that the coefficient of friction is equal to the slope.  However the condition to which they are referring is stated as follows:

• When an object rolls or slides along an incline with acceleration 0 (i.e., moves with constant velocity), the slope of the incline is equal to the coefficient of friction.  (note that this is so for any slope, not just small slopes)

The statement doesn't apply to just any object on any slope.  It only applies to a situation where the acceleration is zero.  It therefore does not apply to the preceding situation.

However the preceding situation can be modified in order to better illustrate the zero-acceleration situation.

• If the slope in the preceding is changed to .03, then the parallel component of the weight is equal in magnitude to the frictional force.
• In this case the net force on an object moving down the incline is zero -.03 mg + .03 m g = 0.  The object will move along this incline with 0 acceleration (and therefore constant velocity), and the coefficient of friction is equal to the slope.
• If the same object coasts up the incline, the net force is -.03 m g - .03 m g = -.06 m g, and its acceleration is -.06 m g / m = -.06 g.

F = 15.5 / x^(3/4)  N cm^(3/4) is just another rule for indicating how a force might vary with the position of an object.

Much in the same way we use F = -k x to find the restoring force exerted by an elastic chain or a spring, we find the force by plugging in value x of the position.

For example if x = 16 cm, we could plug this into the force function F = 15.5 / x^(3/4)  N cm^(3/4) to obtain

F = 15.5 / (16 cm)^(3/4)  N cm^(3/4).  Since (16 cm)^(3/4) = 16^(3/4) cm^(3/4) = 8 cm^(3/4), we get

F = 15.5 / (8 cm^(3/4) ) N cm^(3/4) = 1.93 N * cm^(3/4) / cm^(3/4) = 1.93 N.

From this example we see that the unit N cm^(3/4) in F = 15.5 / x^(3/4)  N cm^(3/4) is just what is necessary in order for our calculation to come out in N.

In the figure below we depict two spheres, meant to represent the Earth and the Moon, each exerting a gravitational force on the other.  Just as with two magnets, these forces are equal and opposite.

If F is the magnitude of the attractive force, with M and m the two masses and r the distance between their centers, then

F = G M m / r^2, with each force being exerted along the line connecting the two centers.

As one object moves toward another, the force on that object is in its direction of motion, so the force does positive work.  The force is conservative, so the work is does it equal and opposite to the PE change of the system.  We conclude that when the objects approach one another the PE change of the system, being equal and opposite the work done by the conservative force, is negative.

The PE of this system, relative to infinite separation, is

PE = - G M m / r.

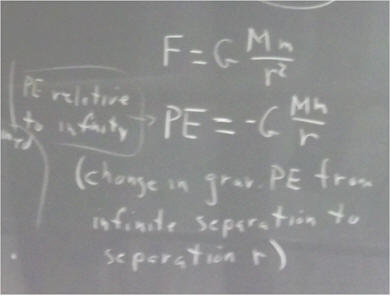
We graph F_grav vs. r for two masses M and m.

• F = G M m / r^2 = (G M m) * (1 / r^2).
• G M m is constant.  The force is therefore a constant multiple of the expression 1 / r^2.
• The graph of 1 / r^2 should be familiar from algebra and precalculus classes.  The graph is symmetric with respect to the y axis, and has vertical asymptotes on both sides of that axis, with horizontal asymptotes at the x axis.  The overall shape of this graph is indicated near top left in the figure below.

A graph of F_grav vs. r is depicted for r > R_earth, where R_earth denotes the radius of the Earth.  (Note that if r < R_earth the mass m would at least partially overlap the Earth, and the equation F = G M m / r^2 would no longer apply.  So we don't extend the graph any further to the left than the point where r = R_earth.)

The work done against gravity as we move one position to another is just the area of the force vs. position graph (recall that the average 'graph altitude' of a trapezoid corresponds to the average force, while the 'width' of the trapezoid corresponds to the change in position, so that the product of the two is the product of average force * displacement).

The shaded region of the graph corresponds to a change in position from r = R_earth to r = 2 * R_earth, and the area of this region corresponds to the work done against gravity to move the object from the first position to the second.

We can approximate the average force exerted between two points as the average (F_1 + F_2) / 2 of the forces at those points.  On the graph shown above we see the two forces depicted and labeled F_1 and F_2.  If a trapezoid was constructed between the two corresponding points of the graph, it should be clear that its average graph altitude would be (F_1 + F_2) / 2.  It should also be clear that the trapezoid would include the shaded region, and that the trapezoid would therefore have greater area (estimating from the depicted graph it appears that the trapezoid would have 10-20% greater area than the region beneath the graph). 

The displacement between R_earth and 2 * R_earth is just R_earth.  It should be clear that this corresponds to the width of our imagined trapezoid.

Our approximation F_ave * displacement will therefore correspond to the area of the trapezoid, which approximates the work done against gravity:

• `dW = (F_1 + F_2) / 2 * R_earth

This result would be our estimate of the change in the potential energy of the mass m as it moved from the surface of the Earth to a point twice as far from the center (we would perceive this point as being one Earth radius 'above' the surface of the Earth).

We could of course use the function to calculate F_1 and F_2, provided we know the mass and radius of the Earth and the second mass m.

The trapezoidal approximation overestimated the area beneath the actual graph, and therefore overestimated the work done against gravity.  The exact result is easily obtained by integration, but this option is only available to students who understand the calculus.

However, while the integration is simple and you should use it if you do have the calculus background, you don't need to do the integration to get the accurate result.  The formula

PE = -G M m / r

comes from the integration (students with a calculus background will verify that the integral of F = G M m / r^2, from r to infinity, is -G M m / r, and that this is the integral that corresponds to the work required to move the mass m from distance r to inifinite distance).

So we could just find the PE_1 and PE_2 (just plug in the two values of r), and subtract.  The result PE_2 - PE_1 will be the change in PE, which corresponds to the work required to move from point 1 to point 2.

preliminary sketch of topics:

Would it have been possible to balance the system at a position where the end with the #8 nuts was higher? Would it have been challenging to do so?
Explain.

We know that for an air cart gliding along an incline, the force that accelerates it is equal to W sin(`theta), where W is the weight of the cart and
`theta the angle of the incline with horizontal. </p>
If the force on the glider was W, what would be its acceleration?</p>
****My answer/question: Wouldn't it be Wsin(`theta)? is that one of those obvious answers?</p>

<h3>acceleration = net force / mass

W sin(theta) is a force, not an acceleration

Since W = m g, though, the net force is

F_net = W sin(theta) = m g sin(theta).

What do you get if you divide this by m?</h3>
 

Also, I have a question about the projectile trials. The ball is going to have a slight v0y since it's coming off the tilted ramp, especially for the
larger slope and I'm not sure how to figure that in right off. That's probably on the site as well but I don't know where.

If you know x, y, x0 and y0, as well as the slope, then since you can easily find the values of sin(theta) and cos(theta) the equations

x = x0 + v0 cos(theta) `dt and
y = y0 + v0 sin(theta) `dt - 1/2 g t^2

can be solved for the two unknowns v0 and `dt.

Eliminate `dt by solving the first equation for `dt, substitute into the second equation, and solve for v0.

Do this symbolically to get a formula that can be easily applied to different trials (I would set it up in Excel).

I'm uncertain about calculating the uncertainty, or percent error. I looked back at my notes from when you were showing us how to do it but I can't make
sense of what I've written. One part shows something like: (a± `da)/(b± `db) using opposite signs on the top and bottom to find the greatest variance.
Then though I have a line connecting to this saying subtract and beside that an addition like 0.2 +0.3 =0.5. The first method really seems to add the most
error by the time you go from time/distance to acceleration, but it seems to be the most logical. Is there somewhere on the site that goes through this or
can you tell me in your response.</p>

<h3>If you know a within uncertainty +-`da, then the proportional uncertainty in a is `da / a. If you multiply this by 100 you get the percent
uncertainty.

If a and b are uncertain respectively by amounts +- `da and +- `db, then the product a * b in a sense really means (a +- `da) * (b +- `db). The product
is a b +- a `db +- b `da +- `da * `db.

If the percent error is small then `da * `db is much smaller than a `db + b `da, and very much smaller than a * b. So the product is approximately ab +-
(a * `db + b * `da).

The proportional uncertainty in ab is therefore (a * `db + b * `da) / (a b) = `db / b + `da / a, which is the sum of the proportional uncertainties in a
and in b.

To you divide a +- `da by b +- `db, you get a similar result. The proportional uncertainties add up.

This is directly related to the product rule. Since the differential d(ab) is equal to da * b + a * db, the quantity ab is uncertain by proportion (da *
b + a * db ) / (ab) = da / a + db / b.</h3>

sweet potato and balancing mass

<h3>The weight vector for the greater mass should be about 12 times as long as for the lesser mass.

Tension forces should be equal, upward on each object, and such that the acceleration has the same magnitude on both sides.</h3>

If parts of the preceding problem gave you trouble, consider an object on an incline with slope .05 and coefficient of friction .03. You can again assume
that since the slope is small, the magnitude of the weight component parallel to the incline is equal to the slope multiplied by the weight of the object,
and also that the normal force does not differ significantly in magnitude from the object's weight. Let m stand for the mass of the object, g for the
acceleration of gravity.

What if the required balancing mass was 200 grams?
****
No, I don’t think it would fit. If the balancing mass was 200g, then that would mean the sweet potato would be heavier.

<h3>the tension would be 200 g * 980 cm/s^2

the gravitational force would be 1188.6 g * 980 cm/s^2

what therefore must be the buoyant force, and how would it compare with the weight of 1 kg of water?</h3>

When a certain object coasts up an incline its acceleration has magnitude 100 cm/s^2 and is directed down the incline. When it coasts down the incline
its acceleration is 50 cm/s^2 and is directed up the incline. Only gravitational, normal and frictional forces are present.

the normal force in this case is equal and opposite to the component of the weight which is perpendicular to the incline

that component is m g sin(theta)

most got greater roc of accel wrt slope with car

Rolling friction has the same magnitude both ways, but acts down the ramp while the ball rolls up, and up the ramp when the ball rolls down.

All other forces remain the same.

So the difference in the frictional forces has double the magnitude of the frictional force.

The difference in accelerations is due to the difference in the frictional forces. So the difference in accelerations is equal in magnitude to the mass *
double the frictional force.

201: start gravitation, show grav sim

what you should know about masses on a rotating system:

velocity is linear, KE isn't, energy is conserved, so 'average point' for KE is not 'average point' for velocity

effect of a given torque can't be linear either (try magnets on rotation wheels, descending mass)