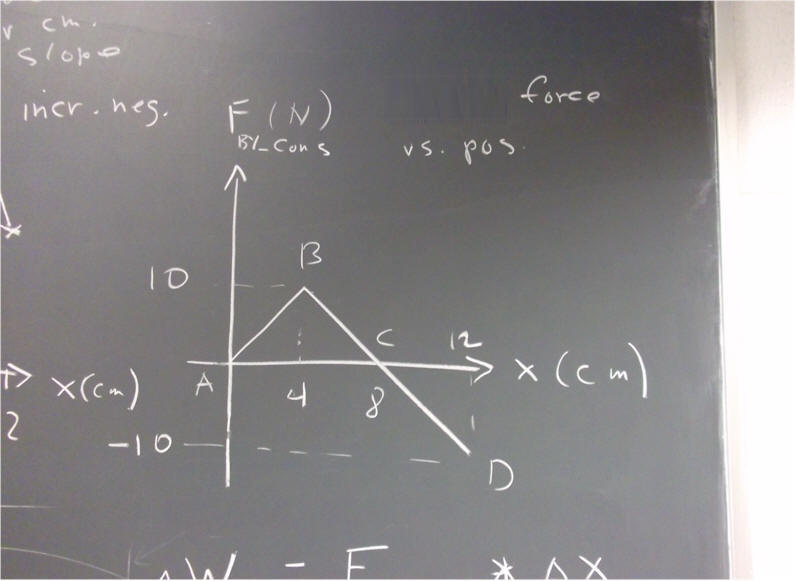
An force function is depicted below, showing the force exerted by a system against conservative forces between positions x = 0 cm and x = 10 cm. 

The force starts out at 0 at point A, increases to 10 N at point B, then decreases linearly to -10 N at point D.

The work done by this force between A and B is calculated below.  The force being a linear function of position on this interval, the average force is the average of the forces at the endpoints of the interval.

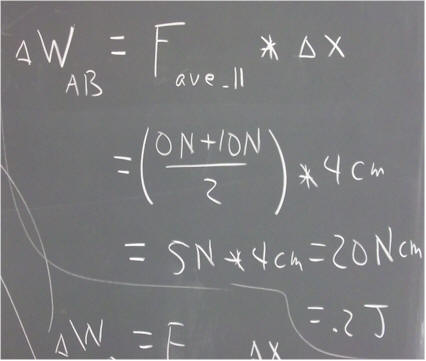
From B to C the force is decreasing, but still positive, so during the positive displacement from B to C, the system again does positive work.

Then from C to D the force becomes negative, and during its positive displacement from C to D the system does negative work.

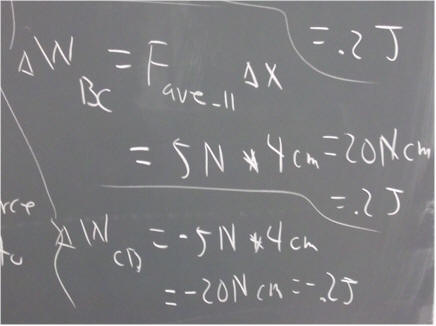
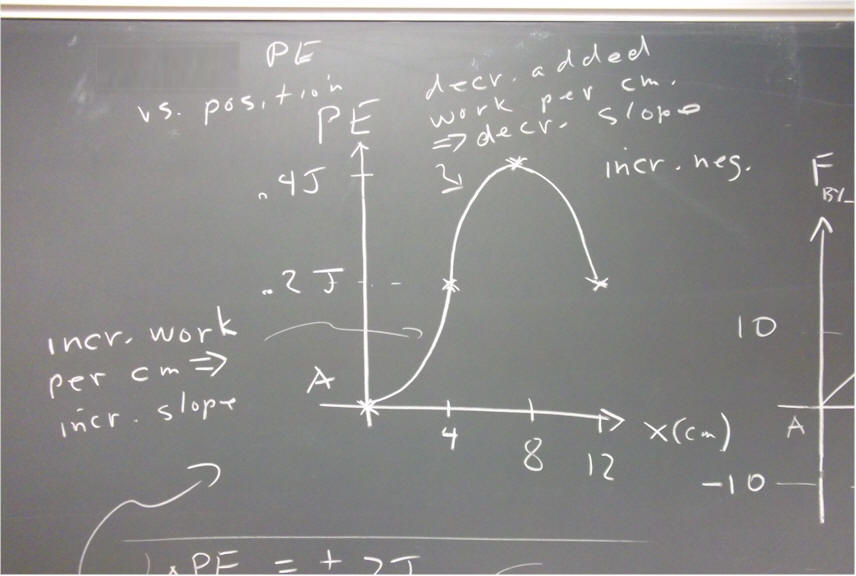
The work done by the system against conservative forces is equal and opposite to the work done by conservative forces on the system, so the work we have calculated is the change in the PE of the system.

We wish to graph the PE vs. position.

• We arbitrarily start with PE = 0 at x = 0.
• Knowing that PE changes by +.2 J between x = 0 and x = 4 cm, by another +.2 J between x = 4 cm and x = 8 cm, and by -.2 J between x = 8 cm and x = 12 cm.

• We conclude that the points (4 cm, .2 J), (8 cm, .4 J) and (12 cm, .2 J) lie on our graph.
• Between 0 cm and 4 cm, the force is increasing, so that with every centimeter the increase in PE is greater than for the preceding cm.  This results in a graph that is concave upward.
• Between 4 cm and 8 cm, the force positive but decreasing, so that with every centimeter the increase in PE is less than for the preceding cm.  This results in a graph that is concave downward.

The question was asked about the meaning of k in the equation PE = 1/2 k x^2.

Consider our F vs. x graph between 0 cm and 4 cm.  Let's assume that this force is exerted against some sort of elastic object, which requires greater and greater force as we extend it further and further from its equilibrium length. 

We analyze the meaning of the slope of that portion of the graph:

• The rise represents the 10 N change in the force on this interval.
• The run represents the 4 cm change in position.
• So slope = rise / run represents `dF / `dx, the average rate of change of the force with respect to position.  Since the graph is a straight line, we can drop the word 'average' and call this the rate of change of force with respect to position.
• This slope is what we call the force constant, which we denote k.
• For this graph the force constant is 10 N / (4 cm) = 2.5 N / cm.  It tells us that the force changes by 2.5 N for every additional cm of stretch.  This is a measure of what we might perceive as the 'stiffness' of the elastic object.

If we apply the formula PE = 1/2 k x^2 to this situation, we get PE = 20 N * cm = .2 Joules. 

• This is identical to the result we obtained earlier for `dW_AB, the work done between points A and B.
• The work done by the system, between the points A and B, is equal to the change in the elastic PE.

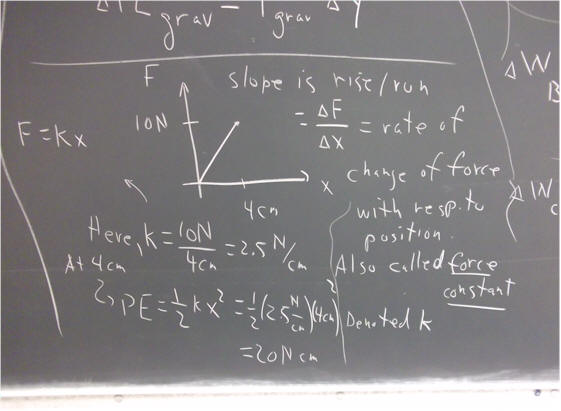
Any time an object of mass m is subject to a linear net force

F_net = - k x

it will, when given a velocity at its equilibrium position and/or when released from a position other than its equilibrium position, oscillate with angular frequency

omega = sqrt( k / m ).

University physics students should be able to derive this result (F_net = m a so - k x = m x '' so x = A cos(omega t + theta_0, where theta_0 and A are arbitrary constants).

We observed an oscillating system during our last class for which we know k is about 30 N / m.  We estimated that the system requires about 1 second to complete an oscillation.  From this information we wish to estimate the mass of the system.

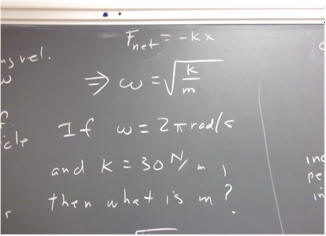
We can solve the equation omega = sqrt(k/m) for m, obtaining m = k / (omega^2).

A cycle corresponds to 2 pi radians of angular displacement, so 1 cycle / second = 2 pi rad / sec.  Using this with our 30 N / m value of k we conclude that

m = (30 N/m) / (2 pi rad/s)^2 = (30 N/m) / (4 pi^2 rad^2 / sec^2) = .75 (N / m) / (rad^2 / s^2)

(N / m) / (rad^2 / sec^2) = (kg m/s^2 / m) * (sec^2 / rad^2) = kg.

We conclude that the mass should be about .75 kg.

Most students estimated the mass to be a little less than, or a little more than a kilogram.  So our result is reasonably consistent with our estimates, meaning that (provided we accept the 30 N/ m estimate of k) our estimates of 1 kg mass and about 1 sec period of motion are reasonably consistent with one another.

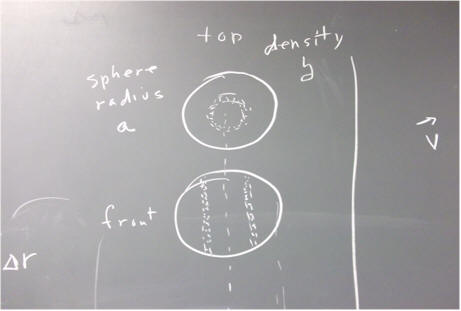
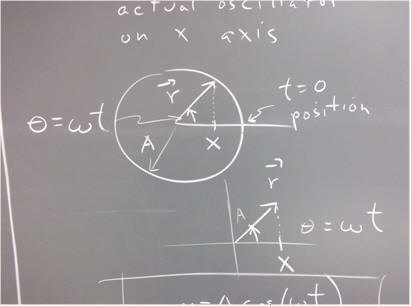
Recall the short lab exercise where we observed the projection onto the tabletop of a point on a CD, as the CD was rotated at 30 degree intervals.  The meaning of the circle shown below, divided up into roughly 30 degree sectors, with the projection to the x axis of the corresponding points on the rim, should be clear in terms of that activity.

Constant angular velocity omega on a reference circle implies that the 30 degree intervals occur at equal intervals of time.

The points on the x axis therefore represent the positions of the x-axis projection points, at equal time intervals. 

If these positions represent the changing position of an actual object, then we can see that the object oscillates back and forth between its extreme points, and furthermore that it moves different distances during different time intervals. 

We can furthermore conclude that the object moves more slowly near the extreme endpoints than near the middle of the interval, and that the maximum speed of the object occurs at the middle point.

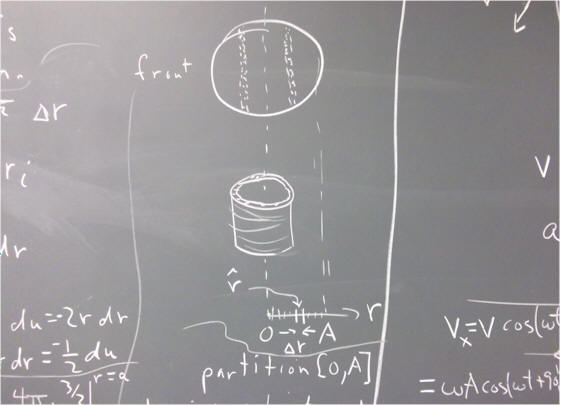
If omega is constant, and if the motion of the reference point (i.e., the point on our circle) begins on the positive x axis at t = 0, then at clock time t the angular position of the point is

theta = omega * t.

Let A represent the radius of our reference circle, r is the position vector describing the position of the reference point as a function of t, then the x projection of r is

x = A cos(theta) = A cos(omega * t).

It follows that the x velocity and acceleration are

v_x = - omega * A sin(omega * t) and

a_x = -omega^2 * A cos(omega * t).

University Physics students (and others who know calculus) can see that these expressions follow immediately from x = A cos(omega * t), by taking two successive derivatives with respect to t.

Most General College Physics and Principles of Physics students will need to simply remember these formulas.  To remember them focus on the following facts:

• omega * t appears as the argument of the sine or cosine function (omega * t is just the angle theta so it makes sense that it should be where it is)
• A doesn't change from one formula to the next
• each formula has a different power of omega. 

Try to also remember the - signs on v_x and a_x.

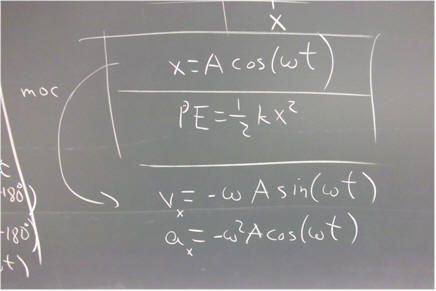
The picture below depicts the r, v and a_cent vectors for the reference-circle point (a_cent is the centripetal acceleration vector).

• v is tangent to the circle, and a_cent points toward the center
• v = omega * A, easily understood by thinking about how a radian relates arc distance to radius
• a_cent = v^2 / r = omega^2 * A.

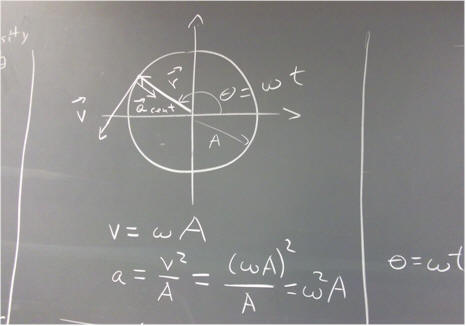
r is at angle omega * t, v is directed 90 degrees counterclockwise from the direction of r and a_cent is in the direction opposite r.

The x component of these respective vectors are the x components of the position, velocity and acceleration of the oscillator moving along the x axis.