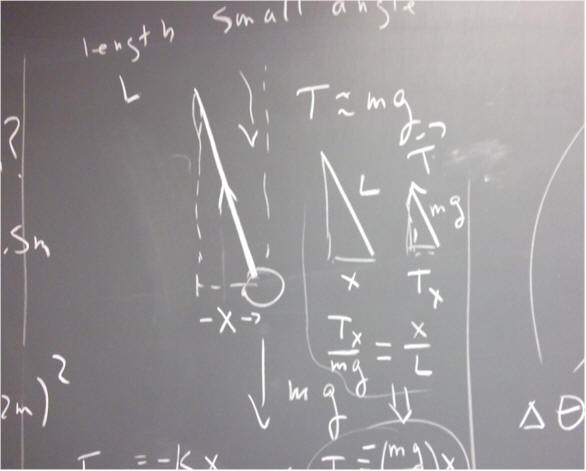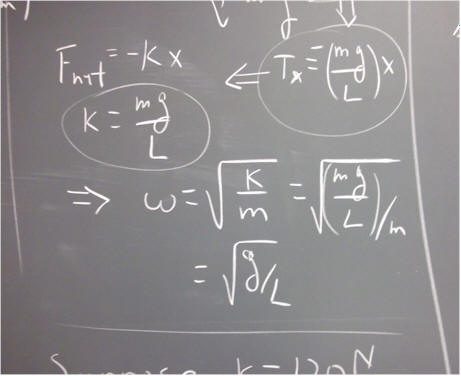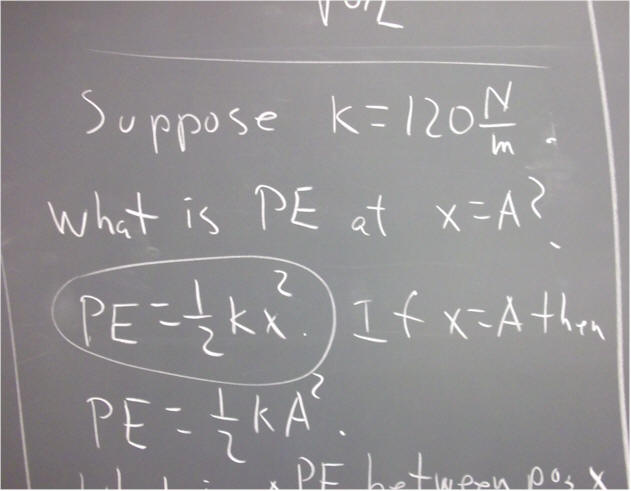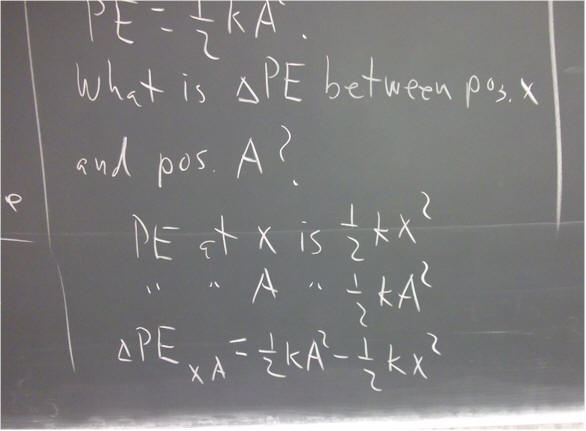101201

From the quantities v0, vf, `dt for uniformly accelerated linear motion we can reason from the definitions to get vAve, `dv, `ds and a.

Similarly from the quantities omega_0, omega_f, `dt for uniformly accelerated angular motion we can reason from the definitions to get omega_Ave, `dOmega, `dTheat and alpha.

This should not be surprising, since the definitions of vAve and aAve are nearly identical (e.g,. for velocity and angular velocity, compare 'average rate of change of position' with respect to clock time with 'average rate of change of angular position with respect to clock time'; the only difference is the word 'angular').  Recall that angular position is measured in units of angle (e.g., revolutions, degrees, radians, half-revolutions, etc.), while linear position is measured in units of length (e.g., cm, meters, etc.).  The most convenient measure of angular position is generally the radian.  Using this measure of angle avoids the need for complicating conversion factors when analyzing the physics and calculus of angular dynamics.

In the case of linear motion, Newton's Second Law relating net force and mass to acceleration amplifies our picture, and motivates our definitions of impulse-momentum and work-kinetic energy (F_net `dt = `d ( m v ), impulse = F `dt, momentum = m v, `dW = F_parallel * `ds, KE = 1/2 m v^2 and `dW_net = `dKE).

In the case of angular motion, Newton's Second Law is expressed in terms of moment of inertia I and net torque tau_net.  This form of Newton's Second Law, combined with the angular quantities we reason out from omega_0, omega_f and `dt, leads us to the angular impulse-angular momentum theorem and the work-kinetic energy theorem for angular motion (tau_net `dt = `d( I omega), angular impulse = tau_net `dt, angular momentum = I omega, `dW = tau_parallel `dTheta , KE_rotational = 1/2 I omega^2, `dW_net_rotational = `dKE_rotational).  Rotational KE has units of energy, and can be converted to and from other forms of translational or rotational KE or PE.  Angular momentum, on the other hand, is a completely new quantity, different from linear momentum.

The structure of the 'flow diagram' for these quantities is identical for the translational and the rotational cases.  The reasoning used to construct one diagram is completely analogous to the reasoning used to construct the other.

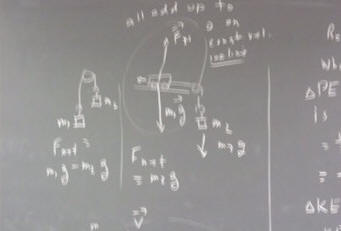
Consider a system consisting of a uniform disk plus a number of discrete masses attached at various points on the disk.  The system rotates about an axis through the center of the disk and perpendicular to its plane.  The total moment of inertia of the system is the sum of the moment of inertia 1/ 2 M R^2 of the disk, and the m r^2 contributions of all the discrete masses.

Calculating the moment of inertia for one such system we find that it is I = .0019 kg m^2. 

The frictional torque is given as .00126 m N, and a force of .09 N acts tangent to the rim of the disk, at a distance of 10 cm from the axis.  The torque exerted by this force is therefore .09 N * .10 m = .009 m * N.  The net torque is therefore the sum of the applied and frictional torques: 

tau_net = .009 m * N + (-.00126 m N) = .0077 m N

This torque is applied for 9 seconds.  This results in angular impulse tau_net * `dt, which by the angular impulse-angular momentum theorem is equal to the change in the angular momentum I * omega.  Since I doesn't change, the change in I * omega is just I * `dOmega, so that

tau_net * `dt = I * `dOmega and

`dOmega = tau_net * `dt / I = .0077 m N * 9 sec / (.0019 kg m^2) = 36 rad / sec.

The units calculation:  m N s / (kg m^2) = m * kg m/2^s * s / (kg m^2) = 1 / s.  Since m / m = rad when the numerator indicates an arc displacement and the denominator indicates a radius, we can say that the result is in rad / s.

`q001.  If a ball rolls on a flat ramp without slipping, then a point on its rim must be rotating about its center with a speed equal to the speed of the ball.  Suppose a ball of radius 20 cm and mass 40 grams is rolling at a speed of 50 cm/s. 

What must be its angular velocity about its axis (hint:  just find the angular velocity of a point on the rim; the whole ball has the same angular velocity)?

What is its moment of inertia?

What therefore is its rotational kinetic energy I omega^2?

What is the ball's translational kinetic energy 1/2 m v^2 of the ball?

What is the total kinetic energy of the ball?

What is the translational kinetic energy as a percent of the total kinetic energy?