Rate of Change definition applied to velocity (from Class Notes 100830)

If you know the time down an incline and the distance, you can easily calculate the average velocity, which is the average rate of change of position with respect to clock time.  By definition of average rate the average velocity is

• ave vel = ave rate of change of position with respect to clock time = (change in position) / (change in clock time).

So for a ball down a ramp, the change in position could be the length of the ramp, the change in clock time the time required to roll from one end to the other.  You would therefore divide the length of the ramp by the time required to roll down the ramp.

The Equations of Uniformly Accelerated Motion (from Class Notes 100901)

This follows the discussion of 'graph trapezoids' in the class notes.

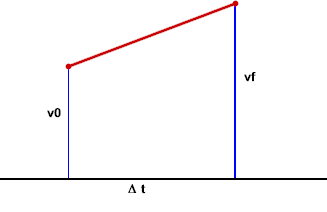
More generally, let us represent the initial and final velocities by the symbols v_0 and v_f, and the time interval by `dt:

The rise between our two points is from v_0 to v_f, a rise of (vf - v0).  The 'run' is the width `dt of the trapezoid, so the slope is

• slope = rise / run = (vf - v0) / `dt

The vertical coordinate of the midpoint is halfway between v0 and vf, so our 'equal-area rectangle' will have height (v0 + vf) / 2, which is the average of the initial and final velocities.  Its width is `dt, so its area is

• area = average height * width = average velocity * time interval = (vf + v0) / 2 * `dt.

The slope represents the acceleration of the corresponding object, and the area represents its displacement, so using a for the acceleration and `ds for the displacement we can write

• a = (vf - v0) / `dt .  We will usually rearrange this equation by solving it for vf, obtaining the equivalent form
• vf = v0 + a `dt.

and

• `ds = (vf + v0) / 2 * `dt.

These equations apply as long as the straight line segment accurately represents the motion of the object during the interval.

These equations involve five quantities:  v0, vf, a, `ds and `dt. 

• If we know three of these quantities, then only two remain unknown.
• With these two equations we will therefore have two unknowns, and we can solve the equations simultaneously to obtain the values of the two unknown quantities.

These equations should not prevent us from directly reasoning out as much of the solution as possible, using the seven quantities vf, v0, vAve, `dv, a, `dt and `ds and the definitions of average velocity and acceleration. 

Most combinations of three of the five variables can be reasoned out without resorting to either of these equations.  Only two combinations (namely, (v0, a `ds) and (vf, a, `ds)) cannot be directly reasoned out using the definitions.  In those cases, we would require several steps to solve the two simultaneous equations.  We can take care of that complication now so we don't have to worry about it later:

We will be doing the algebra during the next class, and we will be writing these steps out using standard notation.  For reference I'm including it here:

We can pretty easily eliminate vf from the two equations:

The equation vf = v0 + a `dt gives us an expression to substitute for vf in the equation `ds = (vf + v0) / 2 * `dt.  We get

`ds = ( (v0 + a `dt) + v0 ) / 2  * `dt.  Simplifying the numerator (v0 + a `dt) + v0 we get

`ds = ( 2 v0 + a `dt) / 2 * `dt.  Dividing the numerator by 2, being sure to use the distributive law, we obtain

`ds =  ( (2 v0) / 2 + a `dt / 2) * `dt = (v0 + 1/2 a `dt) * `dt.  Multiplying through by `dt we get

`ds = v0 `dt + 1/2 a `dt^2.  We will refer to this as the third equation of uniformly accelerated motion.

We can eliminate `dt from the two equations. 

We solve the first for `dt:

a = (vf - v0) / `dt so

`dt = (vf - v0) / a.

We now substitute this expression for `dt in the second equation `ds = (v0 + vf) / 2 * `dt.  We obtain

`ds = (v0 + vf) / 2 * (vf - v0) / a. 

The right-hand side can be written (vf + v0) ( vf - v0) / (2 a).  Since (vf - v0) ( vf + v0) = vf^2 - v0^2, our equation becomes

`ds = (vf^2 - v0^2) / (2 a). 

We could leave the equation as it is, but you will see later that there is good reason to rearrange it as follows:

Multiply both sides by 2 a to get

2 a `ds = vf^2 - v0^2.

Then solve for vf^2, obtaining

• vf^2 = v0^2 - 2 a `ds.

We will refer to this as the fourth equation of uniformly accelerated motion.

Our v vs. t trapezoid therefore gives us four equations that apply to uniformly accelerated motion:

• `ds = (v0 + vf) / 2 * `dt  (we will call this our first equation)
• vf = v0 + a `dt   (we will call this our second equation)
• `ds = v0 `dt + 1/2 a `dt^2  (we will call this our third equation)
• vf^2 = v0^2 + 2 a `ds.  (we will call this our fourth equation)