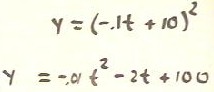Overview_of_sections

Calculus II

Class Notes, 1/08/99

Overview of Sections 6.1 - 6.3

Sections 6.1 - 6.3 contain very little new material. Rather they go into slightly greater depth with topics already covered in the first semester.

Section 6.1 is concerned with creating graphs of antiderivative functions -- i.e., with constructing the graph of f(x), given the graph of f'(x). The main ideas are that

The value of f'(x) at a given x is the slope of the graph of f(x) at that x.
The change in the value of f(x) between two values of x is equal to the area under the graph of f'(x) between those values of x.

Section 6.2 is concerned with constructing antiderivative expressions for given functions and with applying the Fundamental Theorem.

In this section we find antiderivatives for given functions from our knowledge of the derivatives of simple power functions, trigonometric functions and exponential and logarithmic functions.
In a few problems we will encounter relatively simple composite functions and will have to be careful to keep the chain rule in mind.

Section 6.3 is concerned with writing and solving some basic differential equations, mostly in the context of uniformly accelerated motion.

The differential equations encountered will be of the form dy / dx = f(x) for some function f(x); solution will consist of finding the antiderivative y(x) of the function f(x).
The solution function will sometimes have an initial condition, where the value of y is specified for given value of x.

Constructing the graph of f(x) from the graph of f'(x)

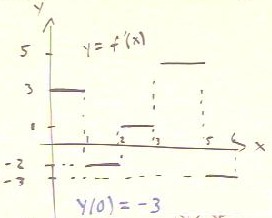
The figure below depicts the graph of a function y = f'(x). We wish to find a graph of y = f(x), subject to the condition y(0) = 3.

We use the fact that the change in the value of the function f(x) between two x values will be equal to the area under the graph of y = f'(x) between these x values.
Between x = 0 and x = 1, we easily see that the area under the y = f'(x) graph is height * width = 3 * 1 = 3.
Between x = 1 and x = 2, we see that the area under the y = f'(x) graph is -2 * 1 = -2.
The corresponding areas between x = 2 and x = 3, and between x = 3 and x = 5, are 1 * 1 = 1 and 5 * 2 = 10.

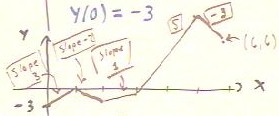
We now construct the graph of y(x), starting with y(0) = -3--i.e., with the point (-3,0).

From the area under the f'(x) graph between x=0 and x=1 we see that f(x) must change by 3 over this interval, so that its value goes from -3 to -3 + 3 = 0. Since f'(x) has constant value 3 on this interval, the y(x) graph will have constant slope 3. You'll see that the graph shown below starts at the point (-3,0) and proceeds along a straight line with slope 3 to the point (1,0).
Over the interval from x = 1 to x = 2 the area under the f'(x) graph is -2, so the change in the y = f(x) graph will be -2. The graph therefore starts the interval at the point (1,0) and ends up at (2, -2); since the f'(x) graph has constant value -2 over this interval the y = f(x) graph will have constant slope -2.
Over the intervals from x = 2 to x = 3, and from x = 3 to x = 5, the changes are similarly found to be 1 and 10, indicating the points (2,-1) and (5,9) on the y(x) graph. The slopes over these intervals are respectively 1 and 5, the values of the f'(x) function over these intervals.
Over the final interval from x = 5 to x = 6, we see that the area under the f'(x) graph is -3, implying a change of -3 in f(x). The change occurs with a constant slope of -3. So we end up the a straight line with slope -3 to the point (6,6).

Finding an Antiderivative Function

Suppose that we wish to find an antiderivative of the function p(`theta) = 3 cos(4 `theta).

We recall from the chain rule that when we take a derivative of sin(4 `theta), we get 4 cos(4 `theta).
So to get a derivative equal to cos(4 `theta), we need to take a derivative of some multiple of sin(4 `theta).
Since the derivative of sin(4 `theta) is 4 cos(4 `theta), to get 3 cos(4 `theta) we need to take the derivative of 3/4 sin(4 `theta).
This is therefore the desired antiderivative.

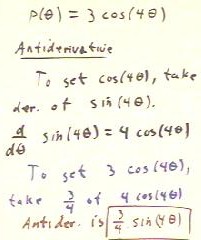
A more formal approach to finding this antiderivative uses a trial function.

The trial function we use here will be c sin(4 `theta).

We know to use this particular trial function because we know from the chain rule that any derivative of sin(4 `theta) will give us a multiple of cos(4 `theta), and that we therefore have only to multiply the sine function by the proper constant to get the desired derivative.
We set the derivative of the trial function c sin(`theta) equal to the function 3 cos(4 `theta) for which we wish to find the antiderivative.
We take the derivative on the left-hand side and obtain an equation we can easily solve for the constant c.
We obtain c = 3/4, so that an antiderivative function is c sin(4 `theta) = 3/4 sin(4 `theta).

As another example we find the general form of the antiderivative of the function t^2 `sqrt(t) + 1 / (t^3 `sqrt(t) ), as indicated in the figure below.

Note that when the antiderivative is written with the integral sign in the form below, we are stating that we wish to find the most general antiderivative possible.

It might seem difficult the find an antiderivative of, say, t^2 `sqrt(t), since this seems to be the product of two functions.
We know that the product rule makes it very unlikely that we can simply find an antiderivative of t^2 and another of `sqrt(t), then multiply them together. So we reject this approach.

The problem becomes relatively easy when we realize that, for example, t^2 `sqrt(t) = t^2 * t^.5 = t^2.5 = t^(5/2).
We can thus rewrite the antiderivative as in the second line below.

At this point we can probably see from our knowledge of power functions that the antiderivative will involve the functions 2/7 t^(7/2) and (-2/5) t^(-5/2).

For illustration, however, we will use a trial function with two constants, c1 and c2, to be evaluated.

We evaluate the constants c1 and c2 using the fact that an antiderivative of t^(5/2) will be some multiple of t^(7/2), which we call c1 * t^(7/2), and that an antiderivative of t^-(7/2) is c2 * t^(-5/2).
We also included an arbitrary constant c in our antiderivative, representing the fact that when we take the derivative, the derivative of c will be 0 and have no effect on our original function.
We therefore use a trial antiderivative function c1 * t^(7/2) + c2 * t^(-5/2) + c.
We set the derivative of this trial function equal to the original function t^(5/2) + t^(-7/2), as in the equation in the fourth line below.
On the left-hand side, after taking the derivative, we obtain the coefficient 7/2 c1 for t^(5/2). Since the coefficient of the t^(5/2) term on the right-hand side is 1, we have 7/2 c1 = 1 and c1 = 2/7.
We similarly see that -5/2 c2 = 1, so c2 = -2/5 (note error: in the last line c2 has been written as -2/7, not -2/5).
Our final antiderivative is therefore as shown in the upper right hand corner of the figure below.

Differential Equations for Freely Falling Objects

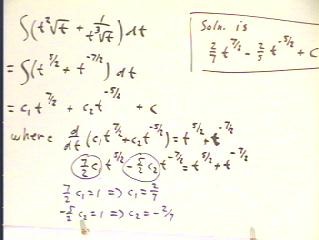
We first recall that acceleration is the rate at which velocity changes. That is, acceleration is expressed by dv / dt.

A freely falling object accelerates downward, in the negative direction (provided we choose the positive direction as up), and the acceleration has magnitude g = 9.8 m/s^2.
Thus for a freely falling object we have dv / dt = -g.
This means that the velocity v of a freely falling object must be an antiderivative of -g.
The most general antiderivative of -g, with respect to clock time t, is -gt + c.
Thus we have v(t) = -g t + c for any freely falling object.

We next recall that the velocity of an object is the rate of change of its position function s(t). That is, v = ds / dt.

In the present example of a freely falling object we have v(t) = -gt + c, with c an arbitrary constant.
Thus we have ds / dt = -gt + c.
It follows that s(t) is an antiderivative of -g t + c.
The most general antiderivative of -gt + c is -1/2 g t^2 + c t + k, where k is an arbitrary constant.
Our position function is therefore s(t) = -1/2 g t^2 + c t + k, with c and k arbitrary constants.

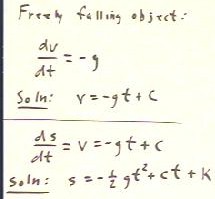
Suppose that we have a situation in which an object falls freely under the acceleration of gravity within initial velocity of -2 meters/second.

These conditions are indicated in the first line below.

The condition on the initial velocity is expressed by v(0) = 2, indicating that initially (i.e., at clock time t = 0) the velocity is -2. This is called an initial condition, as indicated in the figure below.
Since the object is falling freely we have dv / dt = -g = -9.8, indicated simply by the differential equation dv / dt = -9.8 in the second line of the figure below.
The solution to this equation is the antiderivative v(t) = -9.8 t + c.
For this antiderivative function we have v(0) = -9.8 * 0 + c; we note that from the initial condition v(0) is also -2.
We conclude that -9.8 * 0 + c = -2, and that we therefore have c = -2.
It follows that our antiderivative for this specific initial condition is v(t) = -9.8 t + -2, as indicated in the last line below.
This function v(t) = -9.8 t - 2 is therefore our velocity function for initial velocity -2 m/s.

In the preceding example we solved the differential equation dv / dt = -9.8 with initial condition v(0) = -2.

We now solve the equation dy / dx = 4x^3 - 3x, with initial condition y(3) = 5.

Our general solution will be a general antiderivative for 4x^3 - 3x.
We easily find that y(x) = x^4 - 3/2 x^2 + c is a general antiderivative, where c is a constant of integration.
Applying the condition y(3) = 5, we obtain the equation 81 - 27/2 + c = 5.
We easily solve this equation for the integration constant c to obtain c = -62.5.
Our final solution is therefore y(x) = x^4 - 3/2 x^2 - 62.5.

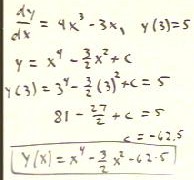
As another example we solve the problem of finding the depth y vs. clock time t for flow from a uniform cylinder.

We find from physics theory and from experiment that the rate at which depth changes is proportional to the square root of the depth.

Depth y therefore satisfies the differential equation dy / dt = k `sqrt(y).

Suppose that we have an initial depth of 100 at clock time t = 0. Then we have the initial condition y(0) = 100.

In order to evaluate the proportionality constant k, we need to know the rate of depth change at some depth.

Let us suppose that the rate of depth change when y = 100 cm is known to be -2 cm/sec. Then we say that when y = 100, dy / dt = -2.

Substituting these quantities into the proportionality we obtain -2 = k `sqrt(100), so that k = -1/5 = -.2.

Our differential equation dy / dt = k `sqrt(y) now becomes dy / dt = -.2 `sqrt(y).

We now have the differential equation dy / dt = -.2 `sqrt(y), with initial condition y(0) = 100.

We cannot solve this equation by simply finding an antiderivative of the right-hand side, because the right-hand side has as its variable y instead of t.
To see this, note that if we tried to say that the antiderivative of -.2 `sqrt(y) is the antiderivative with respect to y, which is -.133 y^(3/2), we would be in trouble because then we would have no idea how to find dy / dt.
Instead we proceed as in the last line of the figure below, algebraically rearranging the equation so that all the y expressions are on one side all the t expressions on the other.

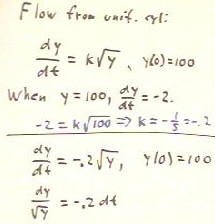
We proceed to find the general antiderivative of both sides of the equation:

An antiderivative of the left-hand side might be 2 `sqrt(y), while an antiderivative of the right-hand side might be - .2 t.
To obtain the most general antiderivative, each side will have an integration constant. However, since these constants are both completely arbitrary, they can be combined on one side of the equation to give a single arbitrary constant.
We therefore finally obtain the equation `sqrt(y) = -.1 t + c; we square both sides to get y = (-.1 t + c) ^ 2.
Applying the initial condition that y(0) = 100, we easily evaluate c, obtaining c = 10.

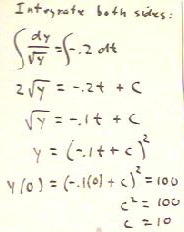
Our final solution is therefore y = (-.1 t + 10) ^ 2.

We can expand the solution into the most familiar quadratic form y = - .01 t^2 - 2 t + 100.
This solution agrees very well with kind of solutions we obtained at the beginning of the first semester for the quadratic models of actual depth vs. time observations.