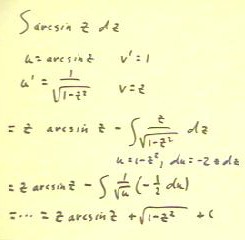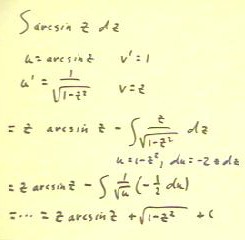
We integrate x / [ (x+5)^2 + 1] using the substitution u = x + 5.

• We do not obtain an x dx in our expression for du, as we might have hoped.
• We therefore solve u = x + 5 for x, so that x = u - 5, which we will substitute for the lonely x.
• We obtain the integral in the fourth line below, which we separate into the two integrals of the fifth line.
• The first of these integrals we perform using a substitution v = u^2 + 1, as indicated; the second we see to be an inverse tangent.
• The integration is easily completed after the last step shown below.

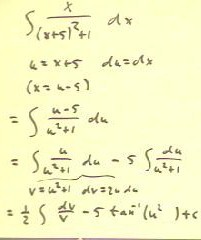
Video Clip #01

We integrate x^4 e^(-3x) using the table, recognizing that our form is that of the integral of p(x) e^(ax).

• We substitute p(x) = x^4 and a = -3 into the form as shown below.
• After factoring out the e^(-3x) we need only reduce the fractions to lowest terms to obtain the final form of the integral.

Video Clip #02

To use the table for the integral of u^5 ln(5u) we first make  the substitution x = 5u, obtaining a multiple of the integral of x^5 ln x.

• Using the integral for x^n ln x in the table, indicated in the upper right corner of the figure, we obtain the expression indicated near the bottom of the figure.
• The last step consists of simplifying the numerical expressions and is straightforward.

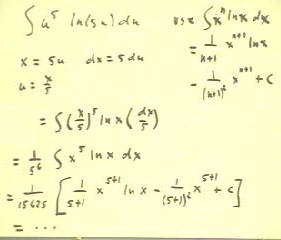
To integrate 1/ sin^2(5`theta) we first substitute u = 5 `theta, obtaining a multiple of the integral of du / sin^2(u).

• We then use the formula for the integral of 1 / sin^m (x) dx, indicated in the upper right-hand corner of the figure.
• Substituting m = 2 we obtain the indicated expression, which simplifies as shown.

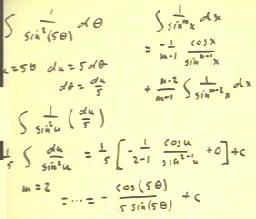
Video Clip #03

The instructions in the text table for integrating sin^m (x) * cos^n (x) say that when m is positive and n negative we expand the denominator using cos^2 (x) = 1 - sin^2 (x).

• The crossed-out second step shows what happens if we follow these instructions. That integral is amenable to any reasonable technique.
• If however we expand the numerator using sin^2 (x) = 1 - cos^2 (x) we obtain the integral in the third line.
• We expand the numerator of this integral as in the fourth line, then separate it into three integrals, each of which we can integrate easily using the tables.

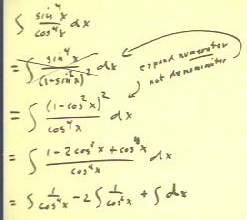
To integrate sin^3 (3 `theta) cos^4 (3`theta) we first substitute u = 3 `theta as shown.

• We obtain the integral shown in the second line.
• Since this integral contains an odd power of the sine function, we leave sin(u) and express the remaining even power of the sine in terms of the cossine function using sin^2(u) = 1 - cos^2(u).
• We obtain the integral in the fourth line which we separate in the fifth line into two integrals, both of which we easily evaluate using the substitution v = cos(u), as indicated.
• The integration of the simple power functions is easily completed.

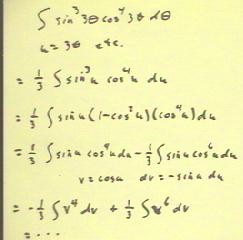
Video Clip #04