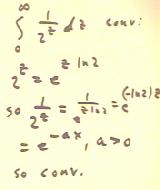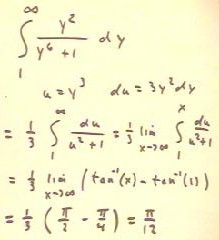Calculus II
Class Notes, 2/08/99
The integral in the figure below is evaluated by first performing a change
a variable u = y^3, as indicated.
- We then express the improper integral as a limit in
the usual manner.
- The limit of tan^-1(x) as x -> infinity is
the angle approached as the tangent of the angle approaches
infinity.
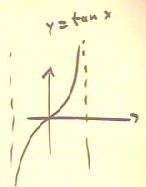
- The graph of the tangent function (second figure)
shows that this angle is `pi/2.
- We thus obtain the values in the last line and the final result `pi/12.
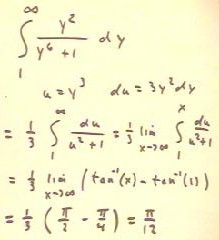
The integral of dx / (x ln(x) ), shown below, is
evaluated by the change of variable u = ln(x).
- After a few straightforward steps we obtain antiderivative ln( ln(x) ), to
be evaluated at x = 2 and x = 1.
- We run into a serious problem when we try evaluate ln ( ln(1)
), since ln(1) = 0 and ln( ln(1) ) = ln(0) is undefined.
- This shows us that we have an improper integral.
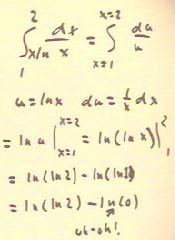
We reevaluate the integral using the limit, as shown
below.
- As y -> 1, ln(y) -> 0; thus the limit of ln
( ln(y) ), as y -> 1, is the limit of ln(z)
as z -> 0. This limit is (-infinity).
- We thus see that the integral approaches infinity in the limit, and
hence diverges.
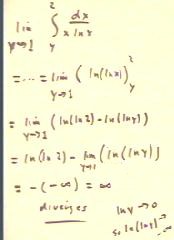
In the figure below we evaluate the integrals of 1
/ x^.9 and 1 / x^1.1, first from 1 to infinity then
from 0 to 1.
The antiderivative of 1 / x^.9 is 10 x^.1.
- Being a positive power of x, this antiderivative approaches
infinity as x -> infinity, so the integral from
1 to infinity will approach infinity and hence diverge.
- Being a positive power of x, this antiderivative
approaches 0 as x -> 0, so the integral
from 0 to 1 is 10 (1^.1) = 10.
The antiderivative of 1 / x^1.1 is -10 x^-.1.
- Being a negative power of x, this antiderivative approaches
zero as x -> infinity, so the integral from 1
to infinity is -10 (1^.1) = -10.
- Being a negative power of x, this antiderivative approaches
-infinity as x -> 0, so the integral from 0
to 1 will approach infinity and hence diverge.
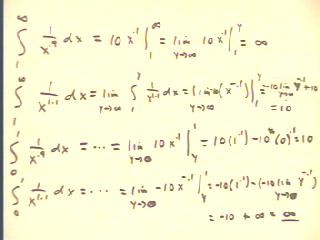
At the top of the figure below we see a graph
of the antiderivative 10 x^.1 of 1 / x^.9.
- The integral of 1 / x^.9 between two x values is
the distance between the corresponding y values of the antiderivative
function.
- The integral from 0 to 1 is therefore indicated
by the vertical arrow from y = 0 to y =
10, as shown.
- The integral from x = 1 to infinity similarly
corresponds to the y arrow from y = 10 to infinity.
In the lower half of the figure below we see the graph
of the antiderivative -10 x^-.1 of 1 / x^1.1.
- The integrals from 1 to infinity and 0 to 1 are
indicated by vertical arrows in a manner similar to that used in the top
figure.

The above integrals show us why the integral of 1
/ x^p, for x = 1 to infinity, diverges if p
< 1 and converges if p > 1.
- Anytime p > 1, we end up with an antiderivative which
is a power function with a negative power and which
therefore approaches zero as x approaches infinity.
- Anytime p < 1, the antiderivative will be a power
function with a positive power and will therefore approach
infinity as x approaches infinity.
These integrals also show us why the integral of 1 / x^p from
0 to 1 must converge if p < 1 and diverge
if p > 1.
- Anytime p > 1 the antiderivative will be a negative
power of x, and will therefore diverge as x
approaches zero.
- Anytime p < 1 the antiderivative will be a positive
power of x, and will therefore approach zero as
x approaches zero.
The integral in the figure below corresponds to the indicated
area under the graph.
The graph has a vertical asymptote at u = -4; its area
might therefore converge or diverge, depending
upon how tightly the asymptote is 'squeezed' to
the vertical line x = -4.
- The change of variable t = u + 4, with the corresponding change
of the limits of integration, shows us that we have the integral
of dt / t^p for p < 1. Since the left-hand
limit is 0, we see that the integral must
therefore converge and the total area remains finite.
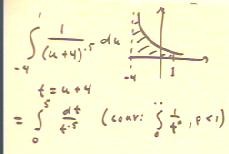
To test the convergence of the integral in the figure
below, we need only note that the integrand is always
< 1 / x^3, which converges.
- If the integrand is less than that of a convergent
integral, the integral must converge.
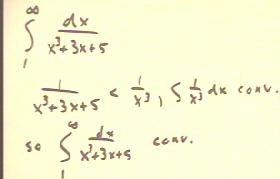
Since 13^z + 5^z > e^z, 1 / (13^z + 5^z) < 1 / e^z - e^-z.
- Since the integral of e^-z converges, the indicated
integral must also converge.

Since 2^z = e^( z ln(2) ), 1/2^z = e^( - ln(2) z) = e^( -a z), with a = ln(2) > 0.
- Since the integral of e^(-a z) converges, so must the integral
of 1 / 2^z.