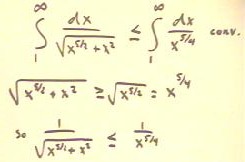Since `sqrt( x^(5/2) + x^2 ) > = `sqrt(x^(5/2)) = x^(5/4), we see that 1 / `sqrt( x^(5/2) + x^2 ) < = 1 / x^(5/4), which is 1 / x^p for p > 1 and therefore converges.

• It follows that the integral in the figure below converges, as indicated.

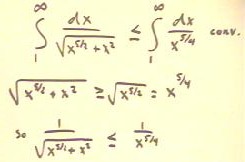
To see that the integral in the figure below converges, we observe that the numerator must lie between 1 and 7, as shown by the graph of the numerator (model by a reference circle of radius three centered at y = 4, as indicated).

• It follows that the given integral is bounded above by the integral of 7 / `theta^3, which is clearly convergent (with denominator `theta ^ p, p > 1).

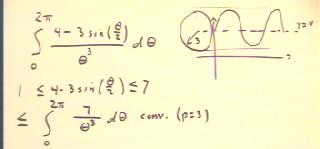
To find an upper bound for the given integral of e^(-x^2), we note that since for x > = 1 we have x^2 > = x, then for x > = 1 we have e^(x^2) > e^x and therefore e^-(x^2) < = e^(-x).

• Then since the integral of e^-x for the given limits is e, we see that the given integral of e^-(x^2) must converge.

We can generalize this result, as shown in the lower right-hand corner, to show that the integral of e^(-x^2) from a to infinity must be < = e^(-a^2) / a.

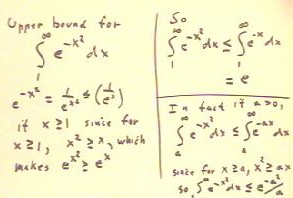
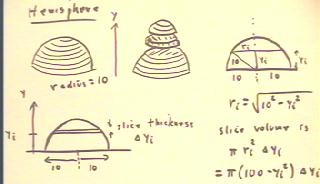
We can determine the volume of a hemisphere of radius 10 by first determining the approximate volume of a horizontal slice with thickness `dyi near altitude yi.

• The approximate volume will be the product of the cross-sectional area of the slice as determined at yi and its thickness.
• The figure at lower left depicts the slice.
• The figure at upper right shows how we can use right triangles to determine the radius of the cross-section at height yi.
• The approximate volume of the slice will therefore be as indicated at lower right.

The total volume of the slices will be the sum of all such slices, indicated by the sum in the figure below.

• The values of yi range from 0 to 10.
• In the limit the integral therefore approaches that shown in the last line of the figure.

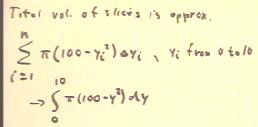
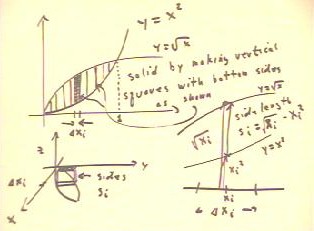
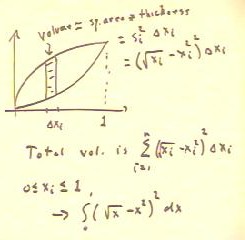
To find the volume of the solid created above the region bounded by the curves y = x^2 and x = `sqrt(x), with the property that each cross-section parallel to the y axis is a square whose base is the segment between the curves, we proceed as in the figure below.

• The sketch at lower left depicts the cross-section of the solid on interval i.
• The volume of the cross-section will be approximately equal to the area of the indicated square and the thickness `dxi.
• To find the length si of the side we use the sample point xi within the ith interval, where the distance from the x axis to the lower curve is xi^2 and to the higher curve is `sqrt(xi).
• The side si extends from the lower curve to the upper and hence has length `sqrt(xi) - xi^2.

The volume lying above the strip indicated in the figure below is therefore the product si^2 `dxi = (`sqrt(xi)^2 - xi^2) `dxi, as indicated below.

• The total volume is obtained by summing over all such strips, where xi ranges from 0 to 1.
• We therefore obtain the integral indicated at the bottom of the figure below.

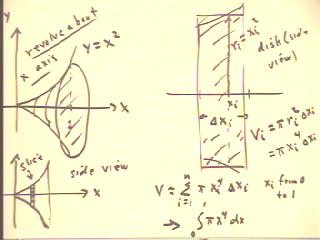
We can rotate the portion of the curve y = x^2 from x = 0 to x = 1 about the x axis, obtaining the horn-shaped solid indicated below.

• We find the volume of this figure by finding the approximate volume of the typical slice of the figure.
• The slice will be a disk with beveled edges; if the slice is sufficiently thin the difference in cross-sectional areas over an individual slice will be small, so the we can approximate the slice by a uniform disk.
• The volume of the disk will be the product of the area of its circular cross-section and its thickness.
• An enlarged view of the ith slice is shown at upper right in the figure below.
• xi is the arbitrary point within the interval at which we determine the radius of the slice, which we will then be used to find the area of the corresponding circular cross-section of the disk.
• The radius will equal the value xi^2 of the function at xi.
• The volume of the disk will therefore be `pi ri^2 `dxi = `pi xi^4 `dxi.
• The total volume will be approximately equal to the sum indicated at bottom right, where xi range from 0 to 1.
• The sum approaches the specified integral.