This experiment uses three calibrated rubbers bands, a paper clip, the 1-foot square of 1/4-inch plywood, three push pins and a paper clip.

NOTE:  This experiment is written for a lab set that includes a piece of thin plywood and push pins.  Your materials might not include these items.  In this case the following substitutions are suggested:

• Instead of the plywood you can use a piece of cardboard; the cardboard should be at least a foot long and 8 inches wide.  The stresses involved are small (less than a pound), so medium-weight cardboard is more than sufficient; lighter weights are often OK, but if the cardboard is too light it might bend.
• If you have push pins of your own you should use them, but if they aren't handy it's not difficult to fold three paperclips into U shapes to make three 'staples', which can then be pushed through the cardboard to hold the ends of the three rubber bands (if you do this be careful; it takes moderate force to push a paper clip through cardboard, and if you have a hand or finger helping out on the other side you can draw blood when the end pushes through).  To hold the system stable you'll want to push them all the way through.

Whatever you use (plywood, cardboard, etc.), you'll want to support it above your tabletop, in order to avoid damaging the tabletop.  A cardboard box works very well for this purpose; so would a couple of books to support the ends of the board.

Set up the experiment:

1.  Print out the grid, which is a .gif file and should give you a printout with 1-cm squares.  (NOTE:  If the 'grid' link doesn't work, or if you prefer to use a PDF, download and/or print grid_1cm).  Place this grid on the plywood square.  (Place an accurate ruler on the grid and verify that the squares indeed line up with the 1-cm marks.  If they don't email the instructor and include the number of millimeters, to the most accurate fraction of a mm you can estimate, by which the grid is off on a 10-cm measurement in the horizontal direction, and the number of mm of error on a 10-cm measurement in the vertical direction.) 

You may also print out a page of rulers.  Be sure to right-click on the page with the rulers, then click on Print.  Otherwise you might print out the top frame of the page, which is not what you want here.  These rulers should be accurate to within a fraction of a millimeter over their 22-cm length.  Measure them and be sure they are indeed accurate.  Note that the markings on these rulers might not be perfect, due to limitations of pixel placement, and that this may  introduce an additional small element of uncertainty in the results of your measurements.

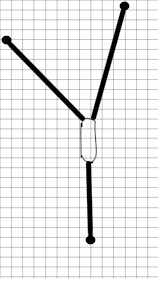
2.  Using a paper clip, three rubber bands and three push pins (or paperclip 'staples') set up the system as shown in the figure below.  In the figure the dark thick lines represent the rubber bands, all three of which are attached directly to the paper clip.  The small circles at the other end of each rubber band represents a push pin (or a  'staple').  The setup should have the following characteristics:

• One rubber band (the one lowest in the figure below) should run along one of the vertical lines of the grid.  In the figure the lowest rubber band isn't quite parallel to the vertical line.  Make sure yours is parallel and that it's on the line.
• Don't let any rubber band exceed its original length by more than 30% (e.g., a rubber band with unstretched length 8 cm should not exceed 10.4 cm in length).  The rubber band most likely to exceed this length will be the one parallel to the vertical grid lines.  Keep an eye on that one as you position the other two.  It would be a good idea to check your calibration graphs to see which rubber band is capable of exerting the most force at the 'plus-30% length', and use that for the 'vertical' rubber band.
• The second rubber band will be directed toward the upper left and will be angled at least 45 degrees to the left of vertical.  This rubber band should stretched to a length that will cause it to exert a force of about 1 Newton.
• The third rubber band should exert enough force to cause the lower rubber band to stretch to at least 20% beyond its maximum unstreched length, but not more than 30% (standard #32 or #33 rubber bands with an initial length of about 8 cm stretch to about 10 cm when supporting about 2 Newtons of weight; if your rubber bands are shorter or stiffer, the lengths may be shorter).  The third rubber band will probably end up closer to vertical than the second rubber band.  Remember that the lower rubber band has to be parallel to the vertical lines.
• It's not shown that way in the picture but you should use paper clips bent into hooks to attach the rubber bands to the push pins.  That will prevent the push pins from 'crushing' the rubber bands and preventing the ends from stretching, and it will also make it much easier to accurately mark the positions of the ends of the rubber bands.  However the 'hooks' can't be too long, or the system won't fit on the board. (If you use paperclip 'staples', as described near the beginning, there is no need to use these 'hooks').

Be very sure that the 'downward' rubber band is stretched to between 10.0 and 10.5 cm, and that it is parallel to the vertical gridlines.

Mark the positions of the ends of the rubber bands, measure their lengths and determine the force exerted by each:

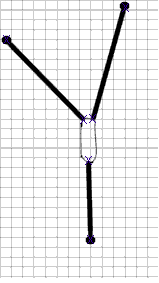
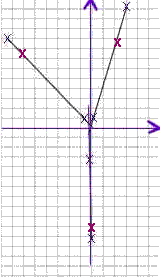
1.  Using a pencil with a good point or a reasonably fine-tipped pen make an x under the end of each rubber band, with the x crossing directly under the very end of the rubber band. Locate this mark as accurately as possible.  The first figure below indicates the positions of the x's (note that the x's under the circles representing push pins will in fact be under hooks at the ends of the rubber bands). 

       

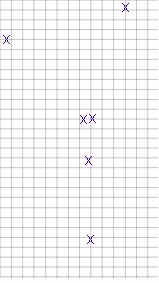
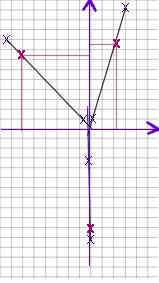
2.  Once you have marked both ends of each rubber band all your information will be on the grid, and you may remove the pins, the rubber bands and the paper clip.   The second figure above shows the grid as it would be with just the x's marked.

3.  Using a ruler measure the length, in cm, of each rubber band, based on the distance between your marked points.

4.  Using the appropriate calibration graph or calibration function determine the force exerted by each rubber band.

In the space below give the length of each rubber band and the corresponding force in Newtons, in this order and separated by a comma:

• In the first line give the information for the 'vertical' rubber band.
• In the second line give the information for the rubber band which slopes up and to the left..
• In the third line give the information for the rubber band which slopes up and to the right.

Starting the fourth line give a brief explanation, in your own words, of what the numbers you have reported mean and how you determined your forces.

Your answer (start in the next line):

#$&*  _ lengths and forces in Newtons _

We will now proceed to calculate the components of the net force using three different methods.  The methods are:

• Graphical determination of force components using sketches of the vectors and projection lines.
• Graphical determination of the resultant vector using the polygon method of vector addition.
• Calculation of components using basic trigonometry (methods of Introductory Problem Set 5).

Graphically determine the components of your forces, using sketches and projection lines:

Set up coordinate axes on the grid, select a point on each line and draw projection lines to determine coordinates; use coordinates to determine angles:

1.  Find the point at which the lines of force meet. For each rubber band use a straightedge to draw a line along the center of the  rubber band's position.   Extend all three lines to their point of intersection.  The first figure below illustrates the lines corresponding to the above figures.

2.  Construct a y vs. x coordinate system whose origin is at the point where the three lines of force intersect, as shown in the second figure below.

      

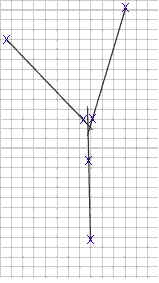
3.  Locate on each line of force the point which is 10 cm from the intersection (i.e., the origin of the coordinate system), as indicated by the heavy red x's in the first figure below.  For each rubber band, just measure 10 cm from the origin, along the line of force.

4.  Sketch the projection line from each of these points to the x and y axes, as shown in the second figure below.  Since one point is already on the y axis it isn't necessary to sketch its projection lines.

     

5.  Determine the x and y coordinate of the point selected on each line of force.   For example in the picture the x and y coordinates of the line in the first quadrant are about 2.3 cm and 8.5 cm, so the point is (2.3, 8.5).  Note that the point (2.3, 8.5) isn't really 10 cm from the origin; when you located your points you hopefully did much better.

Report your results in the space below, x and y in centimeters in comma-delimited format, one rubber band to a line.  Report with the rubber bands in the same order you reported previously. 

Starting in the fourth line, give a brief explanation of how you constructed this graph and how you obtained your results.

Your answer (start in the next line):

 

 

 

#$&*  _ coordinates of points 10 cm from origin along three lines of force _

6.  Find the angle of each line of force by calculating the inverse tangent of the y coordinate divided by the x coordinate (this means inverse tangent of (y coord / x coord), making sure your calculator is in degree mode. For example, for the point (2.3, 8.5) we would get an angle equal to arctan(8.5 / 2.3) = 74.9 degrees, approximately.

On a calculator you can use the inverse tangent function (usually INV and TAN keys, or 2d function and TAN).  Be sure you are in degree mode if you want the angle in degrees, or in radian mode if you want the angle in radians.

If you use Excel you can use the ATAN function (for this angle you would type =ATAN(8.5 / 2.8) into a cell).  Excel gives angles in radians, which you can convert to degrees if you multiply by 180 / `pi (you could just type in = ATAN(8.5 / 2.8) * 180 / PI(), which will give you the angle in degrees.  Note that pi() is Excel's way of denoting `pi).  

7.  Find the angle made by each force vector with the positive x axis, as measured in the counterclockwise direction from the positive x axis.  Note that the angle you found in the preceding instruction is the angle of the line of force with the x axis. 

• The actual force vector might point in either direction along this line.

For example, a line at angle 60 degrees might indicate a force vector into the first quadrant, at 60 degrees as measured counterclockwise from the positive x axis; or the force vector might also point into the third quadrant, making its angle 240 degrees. 

Similarly a line at angle -30 degrees could indicate a vector into the fourth quadrant, at -30 degrees or equivalently at 330 degrees; or it could indicate a vector into the second quadrant, at angle 150 degrees. 

• The rule for the angle of the line with the x axis is arctan(y component / x component).  The angle of a vector (which as indicated above can point in either of two directions along the line) is arctan ( y component / x component), plus 180 deg if the x component is negative.

Report your angles in the space below, one to a line, reporting the rubber bands in the same order as before.  This will require the first three lines.

Starting in the fourth line explain briefly, in your own words, how you obtained your angles.

Your answer (start in the next line):

 

 

#$&* _ angles of three forces

8.  Verify that all your points were really 10 cm from the origin by using the Pythagorean Theorem; i.e., by calculating `sqrt( x^2 + y^2 ), where x and y are the coordinates of the points.  For the point (2.3, 8.5), for example, you would get `sqrt( 2.3^2 + 8.5^2) = 9.2, approx..  The result should be 10.  Obviously whoever located the point on the above graph didn't do a very good job.  Hopefully your results will be better.

Give the results of the Pythagorean theorem in the space below, reporting in each line, in comma-delimited format, the result you obtained and its deviation from the ideal 10 cm.  Report three lines, one for each rubber band, reporting in the same order as previously.

Starting in the fourth line explain what the numbers you have reported mean and how they were obtained.

Your answer (start in the next line):

 

 

#$&* _  pythagorean theorem applied to reported coordinates of three points

Draw to scale the force vectors corresponding to the rubber band forces, determine their components and find their sum.   Note carefully that you are drawing force vectors here, NOT  the lengths of the rubber bands.  You are now done with the lengths of the rubber bands.  Those lengths were only used to find the forces and they are no longer important.

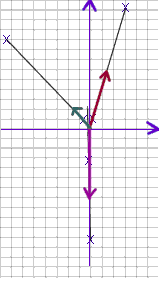
1.  Using a scale of 4 cm per Newton sketch the vector representing the force exerted by each rubber band (the force, not the length of the rubber band). Use a different color or style for the vector corresponding to each rubber band; you might use pens of different colors, or you might use pencil for one, pen for another, and another pen with a different color; or you could use a line which is thicker or thinner than the other lines..

2.  Each vector should have its initial point at the origin, should lie along the line of force and be directed in the direction of the force exerted on the paper clip by the rubber band.  The first figure below illustrates three vectors representing forces of roughly 1.5 Newtons, .6 Newtons and 1.8 Newtons.

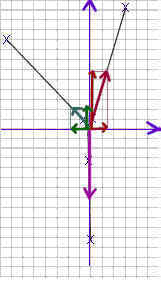
3.  Now draw the projection lines, sketch the component vectors, and validate the components as calculated using the sines and cosines of the angles:  From the tip of each vector sketch the projection lines back to the x axis and to the y axis. Be sure the projection lines run parallel to the grid lines and use a straightedge to locate the projection lines as accurately as possible.

4.  Using the same colors and/or line styles you used to sketch the vectors, sketch the component of each of the force vectors along the x and y axes, as shown in the second figure below.

5.  Measure the length of each of these components, and using the 4 cm to 1 Newton scale determine as accurately as possible how many Newtons are represented by each component.  In the figure below, for example, it looks like the red vector in the first quadrant has components measuring 1.4 cm in the x direction and about 5.8 cm in the y direction.   These forces would correspond to .35 Newtons and 1.45 Newtons.

       

Enter your measurements in the space below.  In each line enter 4 numbers, the first and second being the x and y components of your sketches, in cm, and the second and third being the corresponding x and y forces.  Enter one line for each rubber band, using the same order of rubber bands as before.  Note each quantity you report will be positive or negative, depending on whether that quantity is in the direction of the corresponding axis or opposite the direction of that axis (i.e., right and left are + and -, respectively; up and down are also + and - respectively).

Starting in the fifth line explain briefly what you numbers mean and how you obtained them.

Your answer (start in the next line):

 

 

#$&* _measured lengths of components of vector _ 4 cm / Newton scale

In the space below, report in the first line the total of the x components of all your forces, and in the second line the total of the y components of all your forces.  In the third line explain how you obtained these totals and show the numbers you added to obtain each.

Your answer (start in the next line):

 

 

#$&* _ total of x and of y components

Graphically determine the vector sum by constructing a polygon

Add the three vectors by the polygon method:

1.  Again sketch your three force vectors, this time arranged to form a polygon. Let the terminal point of each vector be the initial point of the next. That is, the vectors should be connected head to tail, as illustrated in the second figure below.

In this figure he polygon runs along the  'red' vector from (0, 0) to (1.4, 6), then from this point along the 'green' vector to about (-.3, 8), then from this point along the 'purple' vector to about (-.3, 1). 

At a scale of 4 cm per Newton, which can also be expressed as 1/4 Newton per cm or .25 Newton per centimeter, the resultant vector has x component -.3 cm * .25 N / cm = -.075 N and y component 1 cm * .25 N / cm = .25 N.

2.  Now sketch a vector from the initial point of the first vector to the terminal point of the last vector.  This vector is the short blue vector in the second and third figures below.  The 'blue' resultant vector originates at (0, 0) and terminates at the third point of the polygon, which we have estimated in the figure below to be at (-.3, 1). 

The fourth figure below indicates the components of this resultant vector, about -.3 cm in the x direction and about 1 cm in the y direction..

What are the coordinates of the resultant vector in your sketch?

       

   

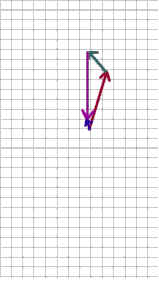
Give the x and y coordinates of the points on your actual graph, in cm, then the x and y coordinates of the corresponding force components, in Newtons, in the first line of the space below, in comma-delimited format.

Starting in the second line give a brief description of your polygon, including the initial and terminal points of each of the vectors in the polygon, and explain how you calculated the force components of your resultant vector using the scale of the graph.

Your answer (start in the next line):

 

 

#$&* _ describe polygon

3.  Are the components of your resultant vector reasonably consistent with the results you got in the preceding activity when you added the components of the vectors?  Answer in the space  below.

Your answer (start in the next line):

 

 

#$&* _ consistency between polygon and adding components

4.  What is the magnitude of the force vector indicated by your sketch?  Use the pythagorean theorem to calculate the magnitude of the resultant force vector, as indicated by the components you gave in the preceding space .  Give your magnitude in the first line, the magnitude calculated by the Pythagorean Theorem in the second, and explain starting in the third line how you calculated it:

Your answer (start in the next line):

 

 

#$&* _magnitude of force vector indicated by measurement _ then by pythagorean theorem on components

Use sines and cosines to find the components of the resultant vector and compare with the results of graphical methods:

Add the three vectors by calculating components:

1.  For each rubber band use the magnitude and the angle of the force it exerts to determine the x and a y component of that force.

• Use the methods of Problem Set 5, using magnitude with the sine and cosine of each angle; i.e., the x component of a force is F cos(theta) and the y component is F sin(theta), where F is the magnitude and theta the angle of the force; you listed these magnitudes and angles early in your report.

List in the space below, using comma-delimited format, the magnitude, angle, x component and y component of each vector.  List one vector per line, in the order of rubber bands used throughout this experiment.  Starting in the third line explain in detail how you calculated the components of the second of these vectors.  Also include a statement comparing the components you calculated with the components you obtained from the scale drawing of the vectors (the one where you used a scale of 4 cm to 1 Newton).

2.  What is the sum of all the x components you calculated in the preceding step? What is the sum of all your y components?

You previously obtained x and y components graphically, first using a sketch and projection lines, then using the polygon method of addition.  Compare your results with the results you obtained before.

In the first line below give, in comma-delimited format, the sum of your x components, as found here, then the sum as found using the first sketch and projection lines, and finally the x component you obtained by the polygon method.  Give in the second line the same information for the sum of the y components.  Beginning in the third line explain what you have done and comment on the relative accuracy of the various methods:

Your answer (start in the next line):

 

 

#$&* _ sum of x comp using sin, cos _ sum using first sketch _ x comp of polygon _ then same for y _discuss relative accuracy

Compare results with ideal result:

Compare what you got with the ideal result:

1.  What is the actual sum of the x components of the forces that actually occurred, in the real world, when you perform this experiment? What is the actual sum of all the y components?

2.  What is the resultant vector corresponding to these components? What is the magnitude of this resultant?

Report the answers to these two questions in the space  below, and explain how you know that your answers must be so:

Your answer (start in the next line):

 

 

#$&* what is actual sum of x comp, y comp  _ what is ideal resultant vector

3.  For each of the three methods of calculating the resultant of the three forces, your error is the magnitude of the difference between the expected result and the actual result, your actual result being the resultant you obtained. Express the magnitude of your error as a percent of the largest of the three force vectors.  Give in the first line the magnitude of your error, and the percent error, for the first graphical method.  In the second line give the same information for the polygon method of addition.  In the third line give the information for your calculations based on magnitudes and angles of the three vectors.

Your answer (start in the next line):

 

 

#$&* _ magnitude of percent error each way as percent of largest force vector _

Your answer (start in the next line):

#$&*

Your answer (start in the next line):

#$&*

Please copy your completed document into the box below and submit the form: