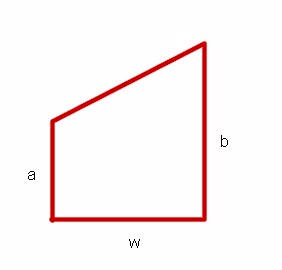
This trapezoid has width w and altitudes a and b.  The width is measured perpendicular to the altitudes.

This particular trapezoid has its altitudes perpendicular to one of the other two legs.  The fourth leg will be called the 'slope segment'.

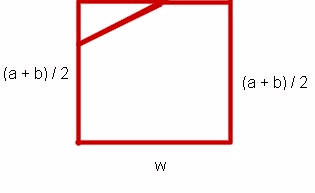
The same trapezoid with a small triangle 'trimmed' at the midpoint of the 'slope segment'.

The trimmed triangle is inverted and appended as shown.  This creates a rectangle whose are is the same as that of the trapezoid.

The altitude of this rectangle is halfway between the two altitudes of the original trapezoid.  Those altitudes were a and b, so the 'midway altitude' would be (a + b) / 2.

The slope of the 'slope segment' is equal to the rise of that segment divided by its run.  The 'slope triangle' is depicted below, a right triangle having width 2 (the 'run') and altitude (b - a) (the 'rise').  The slope is rise / run = (b - a) / w. 

The slope is designated in a rectangular box above the slope segment.

The rectangle formed earlier is superimposed on the trapezoid.  We see that its altitude is equal to the 'midway' altitude (a + b) / 2, the altitude as measured at the midpoint of the slope segment.

The area of the rectangle is thus width * altitude = (a + b) / 2 * w.  This area is designated within an ellipse which is located more or less in the center of the trapezoid.

The traditional definition of the trapezoid has a and b as 'bases'; the condition is that the bases are parallel.  The distance between the bases is generally called the altitude and is generally labeled 'h' rather than 'w' as is done here.  There is no reason to assume that any of the angles of a trapezoid are right angles.  You may search the Web for the usual definition of a trapezoid and the formula for its area.  The usual formula is obtained by a construction very much like the one used here, except that when there are no right angles, it becomes necessary to trim two triangles in order to convert the trapezoid into a rectangle.  The usual formula is area = (a + b) / 2 * h.  This is the same as the formula given here, except that instead of w, h is used for the distance between the parallel sides a and b.

The reason the trapezoid is oriented as shown in the current document is that this orientation and terminology is more appropriate when using trapezoids to approximate the graphs of mathematical functions.