016. `query 16

 

Question: `q 5.4.3 was 5.4.2 fn piecewise linear from (0,1)-(1,1)-(3,-1)-(5,-1)-(6,0). F ' = f, F(0) = 0. Find F(b) for b = 1, 2, 3, 4, 5, 6.What are your values of F(b) for b = 1, 2, 3, 4, 5, 6 and how did you obtain them.

 

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Assessment:

Given Solution:

 ** f(x) is the 'rate function'. The change in the 'amount function' F(x) is represented as the accumulated area under the graph of f(x). Since F(0) = 0, F(x) will just the equal to the accumulated area.

 

We are taking some liberties with the term 'area'.  Area is never actually negative, but in the this solution it is treated as a quantity that can be positive or negative.  There are other terms we could use that would be more accurate, but with this disclaimer we will use the term 'area', including the quote marks, to mean the area of the region which lies above the x axis, minus the area that lies below. 

 

We can represent the graph of f(x) as a trapezoidal approximation graph, with uniform width 1.

 

The first trapezoid extends from x = 0 to x = 1 and has altitude y = 1 at both ends. Therefore its average altitude is 1 and its what is 1, giving area 1. So the accumulated area through the first trapezoid is 1. Thus F(1) = 1.

 

The second trapezoid has area .5, since its altitudes 1 and 0 average to .5 and imply area .5. The cumulative area through the second trapezoid is therefore still 1 + .5 = 1.5. Thus F(2) = 1.5.

 

The third trapezoid has altitudes 0 and -1 so its average altitude is -.5 and width 1, giving it 'area' -.5. The accumulated area through the third trapezoid is therefore 1 + .5 - .5 = 1. Thus F(3) = 1.

 

The fourth trapezoid has uniform altitude -1 and width 1, giving it 'area' -1. The accumulated area through the fourth trapezoid is therefore 1 + .5 - .5 - 1 = 0. Thus F(4) = 0.

 

The fifth trapezoid has uniform altitude -1 and width 1, giving it 'area' -1. The accumulated area through the fifth trapezoid is therefore 1 + .5 - .5 - 1 - 1 = -1. Thus F(5) = -1.

 

The sixth trapezoid has altitudes -1 and 0 so its average altitude, and therefore its area, is -.5. Accumulated area through the sixth trapezoid is therefore 1 + .5 - .5 - 1 - 1 - .5 = -1.5. Thus F(6) = -1.5 **

 

If you made a trapezoidal graph of this function what would be the area of teach trapezoid, and what would be the accumulated area from x = 0 to x = b for b = 1, 2, 3, 4, 5, 6? What does your answer have to do with this question?

 

STUDENT QUESTION:

 

 after reading the solution using the areas of the trapeziods to find the f(x) is clear but but i am not sure where the values
for the altitudes are coming from. I would think that the coordinates given in the problem would be the values you use to
find the altitudes.

INSTRUCTOR RESPONSE:  The value of f (x) is the value of F ' (x), so f(x) is the rate at which the function F(x) changes with respect to x.

On an interval, a linear f(x) forms a trapezoid, which allows us to determine the exact value of the area. The area of the f(x) trapezoid on an interval is the change in the F(x) function on that interval. The reasoning is as follows:

f(x) is the rate at which F(x) changes.

On an interval where f(x) is linear, its average value is equal to the average of its initial and final values. The average value of f(x) on such and interval corresponds to its midpoint value, and represents the average rate of change on the interval.

Multiplying this average value by the 'width' of the interval yields the area of the trapezoid, as can be verified by a simple geometric construction. The width represents the change in x, so the area calculation corresponds to multiplying the average rate of change of F with respect to x, by the change in x. By the definition of rate of change this gives us the change in the value of F(x).

• Thus each trapezoidal area tells us the change in F(x), which we add to the previous value of F(x) (the value at the beginning of the interval) to get the next value (the value at the end of the interval).

 

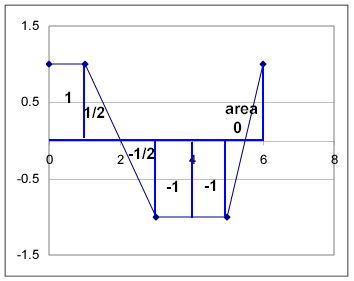
The graph of a function very similar to f(x) is depicted below, with trapezoidal 'areas' indicated.  Note that trapezoidal areas aren't true areas, because areas used in this sense can be negative.

 

From the graph we can read the consecutive 'graph areas' 1, 1/2, -1/2, -1, -1, 0.  Each area gives us the corresponding change in F(x).

 

The function differs from the given function only on the last subinterval, where F(6) = 1 rather than 0.

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question: `q Query 5.4.38 6th; 5.4.35 was 5.4.12. integral of e^(x^2) from -1 to 1.

 

How do you know that the integral of this function from 0 to 1 lies between 0 and 3?

 

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Assessment:

Given Solution:

 ** The max value of the function is e, about 2.71828, which occurs at x = 1. Thus e^(x^2) is always less than 3.

 

On the interval from 0 to 1 the curve therefore lies above the x axis and below the line y = 3. The area of this interval below the y = 3 line is 3. So the integral is less than 3.

 

Alternatively e^(x^2) is never as great as 3, so its average value is less than 3. Therefore its integral, which is average value * length of interval, is less that 3 * 1 = 3. **

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question: `q Query Add comments on any surprises or insights you experienced as a result of this assignment.