If your solution to stated problem does not match the given solution, you should self-critique per instructions at

   http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm

.

Your solution, attempt at solution.  If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it.  This response should be given, based on the work you did in completing the assignment, before you look at the given solution.

002.  The Fundamental Angles.

Goals for this Assignment include but are not limited to the following: 

1.   Construct a unit circle showing all standard angular positions which are multiples of pi/6 or pi/4.

2.  Given starting point and angular velocity model motion on the unit circle.

3.  Relate angular displacement on the unit circle to arc distance and vice versa.

Click once more on Next Question/Answer for a note on

Previous Assignments.

Previous Assignments:  Be sure you have completed Assignment 1 as instructed under the Assts link on the homepage and submitted the result of the Query and q_a_ from that Assignment. 

Question:  `q001.  Note that this assignment has 9 activities. 

If the red ant (review preceding qa if necessary) moves at an angular velocity of pi/6 radians every second, starting from the standard initial point, then what will be its angular position at the end of each of the first 12 seconds?

Your solution: 

Confidence Assessment:

Given Solution: 

The angular position changes by pi/6 radians every second. Starting at angular position 0, the angular positions at t = 1, 2, 3, 4, ..., 12 will be

pi/6, 2 pi/6, 3 pi/6, 4 pi/6, 5 pi/6, 6 pi/6, 7 pi/6, 8 pi/6, 9 pi/6, 10 pi/6, 11 pi/6, and 12 pi/6.

You might have reduced these fractions the lowest terms, which is good. In any case this will be done in the next problem.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q002.  Reduce the fractions pi/6, 2 pi/6, 3 pi/6, 4 pi/6, 5 pi/6, 6 pi/6, 7 pi/6, 8 pi/6, 9 pi/6, 10 pi/6, 11 pi/6, and 12 pi/6 representing the angular positions in the last problem to lowest terms.

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe reduced fractions are pi/6, pi/3, pi/2, 2 pi/3, 5 pi/6, pi, 7 pi/6, 4 pi/3, 3 pi/2, 5 pi/3, 11 pi/6 and 2 pi.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q003.  Sketch a circle centered at the origin of an x-y coordinate system, depicting the angular positions pi/6, pi/3, pi/2, 2 pi/3, 5 pi/6, pi, 7 pi/6, 4 pi/3, 3 pi/2, 5 pi/3, 11 pi/6 and 2 pi. 

What are the angular positions of the following points:

The point 2/3 of the way along the arc between (0,1) and (-1,0)

The point 1/3 of the way along the arc from (0, 1) to (-1,0)

The points 1/3 and 2/3 of the way along the arc from (-1,0) to (0,-1)

The points 1/3 and 2/3 of the way along the arc from (0, -1) to (0,1)??

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe points lying 1/3 and 2/3 of the way along the arc between the points (0,1) and (-1,0) are at angular positions 2 pi/3 and 5 pi/6; the point 2/3 of the way between these points is at angular position 5 pi/6.

The points lying 1/3 and 2/3 of the way along the arc between the points (-1,0) and (0,1) are at angular positions 7 pi/6 and 4 pi/3.

The points lying 1/3 and 2/3 of the way along the arc between the points (0,-1) and (1,0) are at angular positions 5 pi/3 and 11 pi/6.

Note that you should be able to quickly sketch and label this circle, which depicts the angles which are multiples of pi/6,   whenever you need it.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q004.  If the red ant moves at an angular velocity of pi/4 radians every second then what will be its angular position at the end of each of the first 8 seconds?

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe angular position changes by pi/4 radians every second. Starting at angular position 0, the angular positions will be pi/4, 2 pi/4, 3 pi/4, 4 pi/4, 5 pi/4, 6 pi/4, 7 pi/4, and 8 pi/4. You might have reduced these fractions the lowest terms, which is good.In any case this will be done in the next problem.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q005.  Reduce the fractions pi/4, 2 pi/4, 3 pi/4, 4 pi/4, 5 pi/4, 6 pi/4, 7 pi/4, and 8 pi/4 representing the angular positions in the last problem to lowest terms.

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe reduced fractions are pi/4, pi/2, 3 pi/4, pi, 5 pi/4, 3 pi/2, 7 pi/4, and 2 pi.

Self-critique (if necessary):

Self-critique Rating:

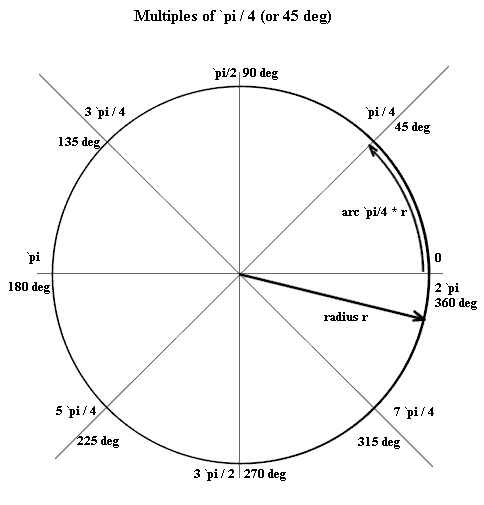
Question:  `q006.  Sketch a unit circle (i.e., a circle of radius 1) centered at the origin of an x-y coordinate system, depicting the angular positions pi/4, pi/2, 3 pi/4, pi, 5 pi/4, 3 pi/2, 7 pi/4, and 2 pi.

What are the angular positions of the following points:

The point 1/2 of the way along the arc between (0,1) and (-1,0)

The point 1/2 of the way along the arc from (0, -1) to (1,0)

The point 1/2 of the way along the arc from (0,-1) to (0, -1)?

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe point lying 1/2 of the way along the arc between the points (0,1) and (-1,0) (the topmost and leftmost points of the circle) is at angular position 3 pi/4.

The point lying 1/2 of the way along the arc between the points (0,-1) and (1,0) is at angular position 7 pi/4.

The point lying 1/2 of the way along the arc between the points (-1,0) and (0,-1) is at angular position 5 pi/4.

These angles are shown in Figure 21.   Note that the degree equivalents of the angles are also given.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q007.  If the red ant starts at angular position pi/3 and moves at an angular velocity of pi/3 radians every second then what will be its angular position at the end of each of the first 6 seconds? Reduce your fractions to lowest terms.

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe angular position changes by pi/3 radians every second. Starting at angular position pi/3, the angular positions after successive seconds will be 2 pi/3, 3 pi/3, 4 pi/3, 5 pi/3, 6 pi/3 and 7 pi/3, which reduce to 2 pi/3, pi, 4 pi/3, 5 pi/3, 2 pi and 7 pi/3.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q008.  Where is the angular position 7 pi/3 located?

Your solution: 

Confidence Assessment:

Given Solution: 

`aIf you have not done so you should refer to your figure showing the positions which are multiples of pi/6. 

On your picture you will see that the sequence of angular positions 2 pi/3, pi, 4 pi/3, 5 pi/3, 2 pi, 7 pi/3 beginning in the first quadrant and moving through the second, third and fourth quadrants to the 2 pi position, then pi/3 beyond that to the 7 pi/3 position. The 7 pi/3 position is therefore identical to the pi/3 position.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q009.  If the red ant starts at angular position pi/3 and moves at an angular velocity of pi/4 radians every second then what will be its angular position at the end of each of the first 8 seconds? Reduce your fractions to lowest terms.

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe angular position changes by pi/4 radians every second. Starting at angular position pi/3, the angular positions after successive seconds will be

pi/3 + pi/4,

pi/3 + 2 pi/4,

pi/3 + 3 pi/4,

pi/3 + 4 pi/4,

pi/3 + 5 pi/4,

pi/3 + 6 pi/4,

pi/3 + 7 pi/4 and

pi/3 + 8 pi/4.

These fractions must be added before being reduced to lowest terms. In each case the fractions are added by changing each to the common denominator 12. This is illustrated for pi/3 + 3 pi/4:

We first multiply pi/3 by 4/4 and 3 pi/4 by 3/3, obtaining the fractions 4 pi/12 and 9 pi/12.

So the sum pi/3 + 3 pi/4 becomes 4 pi/12 + 9 pi/12, which is equal to 13 pi/12.

The fractions add up as follows:

pi/3 + pi/4 = 7 pi/12,

pi/3 + 2 pi/4 = 5 pi/6,

pi/3 + 3 pi/4 = 13 pi/12,

pi/3 + 4 pi/4 = 4 pi/3,

pi/3 + 5 pi/4 = 19 pi/12,

pi/3 + 6 pi/4 = 11 pi/6,

pi/3 + 7 pi/4 = 25 pi/12 and

pi/3 + 8 pi/4 = 7 pi / 3.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q010.  Starting at angular position pi/4 and moving at pi/3 radians / second what will be the resulting positions after each of the first 6 seconds?

Your solution: 

Confidence Assessment:

Question:  `q011. Starting at angular position 0, the angular positions at t = 1, 2, 3, 4, ..., 12 will be

pi/6, 2 pi/6, 3 pi/6, 4 pi/6, 5 pi/6, 6 pi/6, 7 pi/6, 8 pi/6, 9 pi/6, 10 pi/6, 11 pi/6, and 12 pi/6.

So after 12 seconds we will have moved through an arc of 12 pi / 6 radians.  Since 12 pi / 6 reduces to 2 pi, we will have moved through an arc of 2 pi radians, and we will be back at our starting point.

If we continue to move around the circle for one more second we will have moved, in 13 seconds, through a total angle of 13 pi / 6 radians, and we will be at the same point on the circle as when we had moved through pi/6 radians.

Through what total angle will we have moved by the end of each of the next 4 seconds, and at what previously visited point on the circle will we be located at the end of each?

Your solution: 

Confidence Assessment:

Question:  `q012.  This is an optional challenge question.  If we start from angular position 0 and move through 7 pi / 4 radians every second, through what total angle will we have moved and where on the circle will we be at the end of each of the first 4 seconds?

Your solution: 

Confidence Assessment: