If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
005. The graph keeps going and going. Thru what coordinates on the t axis does it pass etc
Goals for this Assignment include but are not limited to the following:
1. Construct a table of the values of y = A sin(x) for a given value of A, construct a graph of a single cycle of this function, then extending the graph forward and/or backward for any specified number of complete cycles.
2. Given a function y = A sin(theta) with theta given as a function of x, construct a y vs. x graph of a single cycle of this function, then extending the graph forward and/or backward for any specified number of complete cycles.
3. Interpret the function and graph corresponding to Goal 2 in terms of angular motion on a circle of appropriate radius.
Click once more on Next Question/Answer for a note on Previous Assignments.
Previous Assignments: Be sure you have completed Assignment 4 as instructed under the Assts link on the homepage and submitted the result of the Query and q_a_ from that Assignment.
Question: `q001. If the red ant keeps traveling around the circle (e.g., assume an immortal though mindless red ant that has been traveling around the circle since before time began and will continue until time ends, whatever that means, traveling continually without pause or change in speed) then its y coordinate will go from 0 to 1 to 0 to -1 to 0, then to 1 to 0 to -1 to 0 again and again and again, endlessly repeating the cycle. A graph of y vs. theta will therefore alternates peaks at 1 and valleys at -1. By how much does theta change from one peak of the graph to the next?
Your solution:
Confidence Assessment:
Given Solution:
`aThe peak of the graph corresponds to the angular position pi/2, at the 'top' of the circle. In order for the graph to get from one peak to the next, the ant must travel from the top of the circle all the way around until it reaches the top once more. The angular displacement corresponding to a circuit around the circle is 2 pi. The angle theta on the graph therefore changes by 2 pi between peaks.
Self-critique (if necessary):
Self-critique Rating:
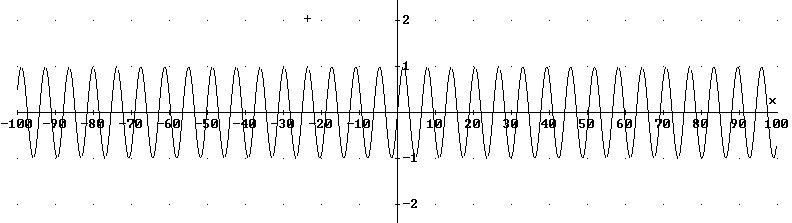
Question: `q002. The graph of the basic sine function is centered on the theta axis, running in both the positive and negative directions, never ending, always repeating with a period of 2 pi. The graph represents never-ending motion around the unit circle with angular velocity 1, extending back forever, extending for forever. That is, extending forever into the past and forever into the future. How many complete cycles of the sine function will be completed between theta = -100 and theta = 100?
Your solution:
Confidence Assessment:
Given Solution:
`aBetween theta = -100 and theta = +100 the change is 100 - (-100) = 200. Since the complete cycle is completed as theta changes by 2 pi, the graph will complete 200 / (2 pi) = 100 / pi = 31.8 cycles, approximately. This corresponds to 31 complete cycles.
However there is be another way of answering this question. If a complete cycle is defined as the cycle from y values 0 to 1 to 0 to -1 and back to 0, then between theta = 0 and theta = 100 there are 15.9 cycles, or 15 complete cycles, and moving to the left, between theta = 0 and theta = -100 there are another 15 complete cycles. This totals only 30 complete cycles.
The answer to the question therefore depends on just where cycles are considered to begin.
See Figure 25. If you count 'valleys' from the far left to the far right you find that there are 32 'valleys' so that the function completes 31 cycles between theta = -100 and theta = 100. However if you count complete cycles from the origin moving to the right you find only 15, and the same number from the origin moving to the left, so in that sense there appear to be only 30 cycles.

Self-critique (if necessary):
Self-critique Rating:
Question: `q003. The graph of y = sin(3 t) represents the y coordinate of motion around the arc of the unit circle at 3 units per second. This graph of y vs. t can, just as in the preceding problems, continue forever into the past and into the future. What will be the distance between the peaks of this graph?
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance between peaks corresponds to the time required for the ant to complete a cycle around the circle. The ant moves around the unit circle, which has circumference 2 pi. At 3 units per second the time required is 2 pi / 3 seconds. The peaks of the graph will therefore be separated by 2 pi / 3 units along the t axis.
Self-critique (if necessary):
Self-critique Rating:
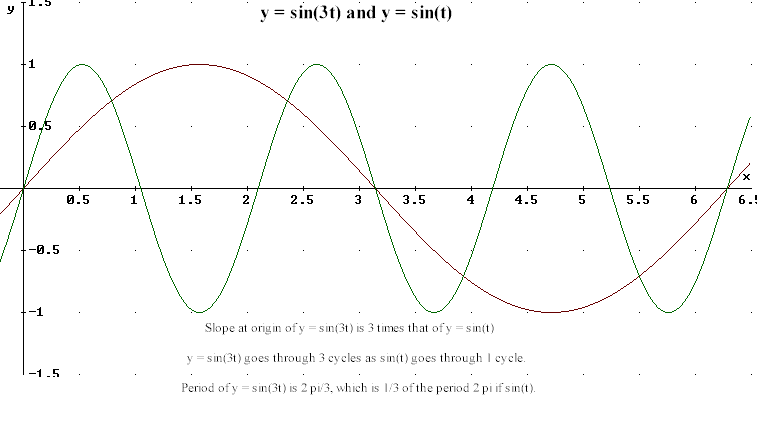
Question: `q004. The graphs of y = sin(3 t) and y = sin(t) both go through the origin and both with positive slope. Which graph goes through the origin with a greater slope?
Your solution:
Confidence Assessment:
Given Solution:
`aAs shown in Figure 41, the graph of y = sin(3t) has the same y values but the horizontal distance between peaks is 1/3 that of the y = sin(t) graph. This compression of the graph triples the slopes, so the graph of y = sin(3t) has three times the slope at corresponding points compared to the graph of y = sin(t).
The graphs do correspond at the origin, so the slope of the y = sin(3t) is three times as great at the origin as the slope of the graph of y = sin(t).
Self-critique (if necessary):
Self-critique Rating:
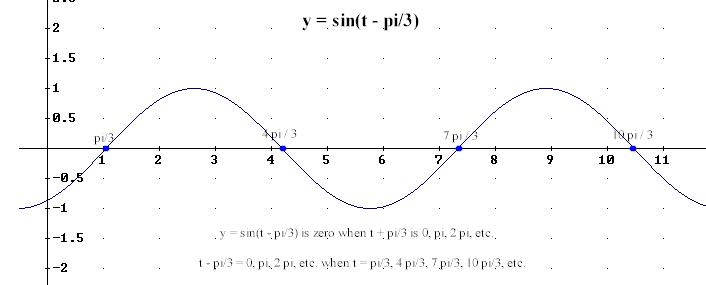
Question: `q005. Through what coordinates on the t axis does the graph of y = sin(t - pi/3) pass? Through what points on the t axis does the graph pass in the interval 0 <= t <= 2 pi? Does this graph pass through the origin?
Your solution:
Confidence Assessment:
Given Solution:
`aThe graph of y = sin(theta) passes through the horizontal axis when the reference circle position is at tthe circle meets the x axis. This occurs repeatedly, at angular positions theta = 0, pi, 2 pi, 3 pi, 4 pi, etc.; and also at angular positions theta = -pi, -2 pi, -3 pi, etc..
If we are considering the graph of y = sin(t - pi/3) then when theta = t - pi/3 takes values 0, pi, 2 pi, 3 pi, ..., we see that t = theta + pi/3 takes values t = 0 + pi/3, pi + pi/3, 2 pi + pi/3, etc.. These values simplify to give us
t = pi/3, 4 pi/3, 7 pi/3, ... .
A graph is shown in Figure 91. Note that only the values t = pi/3 and t = 4 pi/3 lie between 0 and 2 pi.
Self-critique (if necessary):
Self-critique Rating:
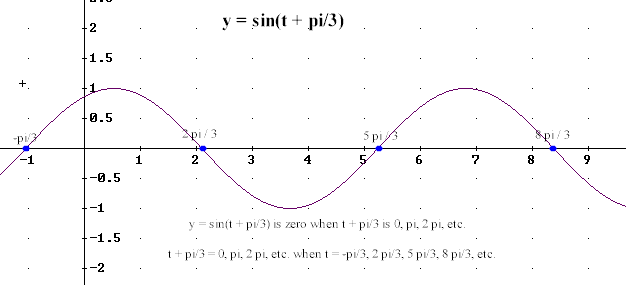
Question: `q006. Through what coordinates on the t axis does the graph of y = sin(t + pi/3) pass? Through what point on the t axis does the graph pass in the interval 0 <= t <= 2 pi? Does this graph pass through the origin?
Your solution:
Confidence Assessment:
Given Solution:
`aThe graph of y = sin(theta) passes through the horizontal axis when the reference circle position is at the rightmost or leftmost point, one of the points for the circle meets the x axis. This occurs repeatedly, at angular positions theta = 0, pi, 2 pi, 3 pi, 4 pi, etc.; and also at angular positions theta = -pi, -2 pi, -3 pi, etc..
If we are considering the graph of y = sin(t - pi/3) then when theta = t + pi/3 takes values 0, pi, 2 pi, 3 pi, ..., we see that t = theta - pi/3 takes values t = 0 - pi/3, pi - pi/3, 2 pi - pi/3, etc.. These values simplify to give us
t = -pi/3, 2 pi/3, 5 pi/3, 8 pi/3, ... .
The graph is shown in Figure 91. Only the values t = 2 pi/3 and t = 5 pi/3 lie between 0 and 2 pi.

Self-critique (if necessary):
Self-critique Rating:
Question: `q007. What are the first four t coordinates at which the graph of y = sin(t - pi/3) passes through the t axis, for t > 0?
Your solution:
Confidence Assessment:
Given Solution:
`aThe graph of y = sin(theta) passes through the horizontal axis when the reference circle position is at the rightmost or leftmost point, one of the points for the circle meets the x axis. This occurs repeatedly, at angular positions theta = 0, pi, 2 pi, 3 pi, 4 pi, etc.; and also at angular positions theta = -pi, -2 pi, -3 pi, etc..
If we are considering the graph of y = sin(t - pi/3) then when theta = t - pi/3 takes values 0, pi, 2 pi, 3 pi, 4 pi, ..., we see that t = theta + pi/3 takes values t = 0 + pi/3, pi + pi/3, 2 pi + pi/3, 0 + 4 pi / 3. These values simplify to give us
t = pi/3, 4 pi/3, 7 pi/3, 10 pi/3, ... .
These are the first four positive values of t for which the graph passes through the t axis.
Self-critique (if necessary):
Self-critique Rating:
Question: `q008. What are the first four positive t coordinates through which the graph of y = sin(t + pi/3) passes through the t axis, for t > 0?
Your solution:
Confidence Assessment:
Given Solution:
`aThe graph of y = sin(theta) passes through the horizontal axis when the reference circle position is at the rightmost or leftmost point, one of the points for the circle meets the x axis. This occurs repeatedly, at angular positions theta = 0, pi, 2 pi, 3 pi, 4 pi, etc.; and also at angular positions theta = -pi, -2 pi, -3 pi, etc..
If we are considering the graph of y = sin(t - pi/3) then when theta = t + pi/3 takes values 0, pi, 2 pi, 3 pi, ..., we see that t = theta - pi/3 takes values t = 0 - pi/3, pi - pi/3, 2 pi - pi/3, 3 pi - pi/3, 4 pi - pi/3, etc.. These values simplify to give us
t = -pi/3, 2 pi/3, 5 pi/3, 8 pi/3, 11 pi/3, ... .
The first four positive values of t for which the graph passes through the t axis are 2 pi/3, 5 pi/3, 8 pi/3 and 11 pi/3. The corresponding graph is shown in Figure 9.
Self-critique (if necessary):
Self-critique Rating:
Question: `q009. Through what coordinates on the t axis does the graph of y = sin(3t + pi/3) pass? Through what point on the t axis does the graph pass in the interval 0 <= t <= 2 pi? Does this graph pass through the origin?
Your solution:
Confidence Assessment:
Given Solution:
`aThe graph of y = sin(theta) passes through the horizontal axis when the reference circle position is at the rightmost or leftmost point, one of the points for the circle meets the x axis. This occurs repeatedly, at angular positions theta = 0, pi, 2 pi, 3 pi, 4 pi, etc.; and also at angular positions theta = -pi, -2 pi, -3 pi, etc..
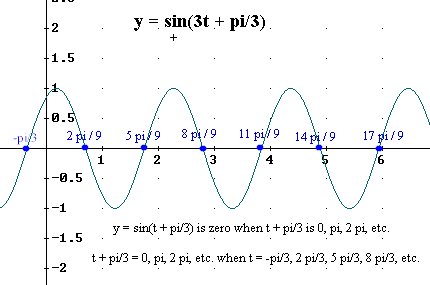
If we are considering the graph of y = sin(3t + pi/3) then when theta = 3t + pi/3 takes values 0, pi, 2 pi, 3 pi, ..., we solve for t in order to see that t = theta/3 - pi/9 takes values
t = 0/3 - pi/9, pi/3 - pi/9, 2 pi/3 - pi/9, 3 pi/3 - pi/9, 4 pi/3 - pi/9, ..., n pi/3 - pi/9, ..., where n = 0, 1, 2, 3, ... . These values simplify to give us
t = -pi/9, 2 pi/9, 5 pi/9, 8 pi/9, 11 pi/9, ... .
If we list these values starting with the first positive value 2 pi/9, continuing as long as t < 2 pi, we obtain values 2 pi/9, 5 pi/9, 8 pi/9, 11 pi/9, 14 pi/9, 17 pi/9. Since 2 pi = 18 pi/9 any subsequent solution will be greater than 2 pi so is not included. The corresponding graph is shown if Fig 66.
Complete Assignment 4, including Class Notes, text problems and Web-based problems as specified on the Assts page.
When you have completed the entire assignment run the Query program. Submit SEND files from Query and q_a_.