If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
006. Basic triangles; Inverse Functions
Goals for this Assignment include but are not limited to the following:
1. Construct the basic triangles corresponding to angles pi/6, pi/4, pi/3, as appropriate, in order to find the sines and cosines of these angles.
2. Using exact values construct tables and graphs for the basic trigonometric functions.
3. Using exact values construct y vs. x graphs of y = A sin(theta) or y = A cos(theta), where theta is given as a function of x.
4 . Use the technique of reversing columns and restricting domain to construct tables and graphs for the arcsin and arccos functions.
5. Given an equation in which the argument of the sine or cosines function is a function of x, solve the equation for all values of x within a given interval.
Click once more on Next Question/Answer for a note on Previous Assignments.
Previous Assignments: Be sure you have completed Assignment 5 as instructed under the Assts link on the homepage and submitted the result of the Query and q_a_ from that Assignment.
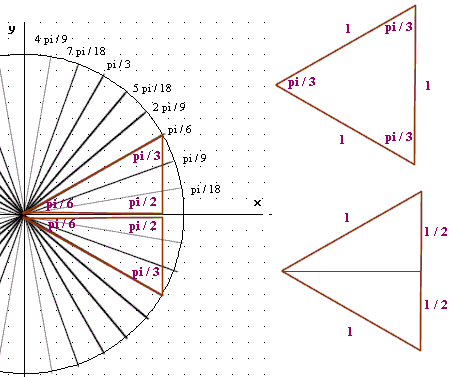
Question: `q001. Construct the triangle corresponding to the pi/6 angular position:
Sketch a segment from the origin to the pi/6 position on the circle, then straight down to the x-axis and back along the x-axis to the origin.
Sketch also the triangle corresponding to the theta = -pi/6 position, sketching a segment from the origin to the -pi/6 position on the circle, then straight up to the x-axis and back along the x-axis to the origin.
What are the three angles in each of the two triangles you have constructed?
The two triangles you have sketched join to form a larger triangle. Describe the larger triangle. How do the lengths of the sides of this larger triangle compare?
Your solution:
Confidence Assessment:
Given Solution:
Figure 2 shows the construction of these triangles on a unit circle, whose radius is 1. The angle made by the vertical and the horizontal sides of each triangle is a right angle of pi/2 radians. The remaining two angles must add up to a right angle, and since the central angle of each triangle is pi/6 the other angle is pi/3.
These two triangles naturally join to form a larger triangle, which is easily shown to be an equilateral triangle:
The central angle of the larger triangle is pi/6 + pi/6 = pi/3. The other two angles are also pi/3, so the triangle is equiangular. If the triangle is rotated through an angle of pi/3 it coincides with itself, and this symmetry implies that the triangle is equilateral. Therefore the three sides of the larger triangle are equal.

Self-critique (if necessary):
Self-critique Rating:
Question: `q002. What therefore is the length of the vertical side of each of the two original triangles?
Your solution:
Confidence Assessment:
Given Solution:
`aThe vertical side of the equilateral triangle is formed from the vertical sides of the two original triangles. Since the original two triangles are congruent it follows that the vertical side of each is 1/2 the side of the equilateral triangle. Since every side of the equilateral triangle is 1, it follows that the vertical sides of the original triangles are each 1/2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q003. Each of the original triangles has hypotenuse 1 and vertical leg 1/2. By the Pythagorean Theorem, what therefore is the length of the horizontal side of either triangle?
Your solution:
Confidence Assessment:
Given Solution:
`aBy the Pythagorean Theorem c^2 = a^2 + b^2, where a and b are the legs and c the hypotenuse of a right triangle. Thus b^2 = c^2 - a^2 so that b = sqrt(c^2 - a^2). In the case of this triangle, if a = 1/2 and c = 1 we get b = sqrt(1^2 - (1/2)^2) = sqrt(1 - 1/4) = sqrt(3/4)= sqrt(3) / 2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q004. What therefore is the y coordinate of the point on the unit circle corresponding to angular position pi/6? What is the x coordinate?
Your solution:
Confidence Assessment:
Given Solution:
The triangle is depicted in Figure 65. The y coordinate is 1/2 and the s coordinate is sqrt(3) / 2. The unit-circle point corresponding to angular position pi/6 is (sqrt(3)/2, 1/2), as indicated in Figure &&. Note that the approximate coordinates, accurate to 2 significant figures, are the values we used previously for this angle so that the approximate coordinates are (.87, .5).

Self-critique (if necessary):
Self-critique Rating:
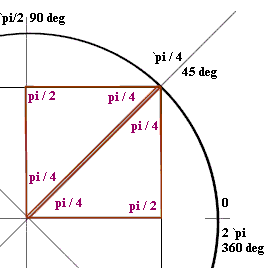
Question: `q005. Construct the angle corresponding to the angular position pi/4. Starting at the origin draw a line out to the pi/4 position, then directly down to the x axis and finally back along the x axis to the origin; this will form a triangle. Draw another triangle, this time starting from the origin, go into the pi/4 point, then straight back to the y-axis along horizontal line, and finally down the y-axis to the origin. What are the three angles in each triangle? How do the lengths of the two legs of each triangle compare? When these two triangles are put together what shape do they form?
Your solution:
Confidence Assessment:
Given Solution:
`aThe triangles are shown in Figure 46. Each triangle has a horizontal and a vertical side, so one of the angles formed is a right angle pi/2. The central angle in each is pi/4, so it follows that the remaining angle, in order that the three angles add up to pi, is also pi/4.
These triangles, having two equal angles, are therefore both isosceles, with equal legs.
The two triangles form a square, since the sides of the combined figure are all horizontal or vertical and since the equal legs form the sides.
If the entire figure is flipped about the theta = pi/4 line there will be no change except that the x and y sides will be interchanged. The interchanged triangles will coincide, but the x and y sides of the triangles will be interchanged, showing that the x and y coordinates of the two triangles are the same.
Self-critique (if necessary):
Self-critique Rating:
Question: `q006. If the circle has radius 1 it follows that the hypotenuse of either triangle is 1. Let s stand for the lengths of the (equal) legs of either triangle. By the Pythagorean Theorem what must therefore be the length of the side s?
Your solution:
Confidence Assessment:
Given Solution:
Figure 23 shows the first triangle with the legs labeled s and the hypotenuse 1.
The Pythagorean Theorem tells us that s^2 + s^2 = 1, so that 2 s^2 = 1 and s^2 = 1/2. From this we get s = 1 / sqrt(2) = sqrt(2) / 2.
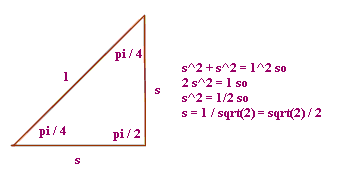
Self-critique (if necessary):
Self-critique Rating:
Question: `q007. What therefore is the y coordinate of the point corresponding to angular position pi/4? What is the x coordinate?
Your solution:
Confidence Assessment:
Given Solution:
`aThe y coordinate is the same as the x coordinate, sqrt(2) / 2. The unit-circle point corresponding to angular position pi/4 is therefore (sqrt(2) / 2, sqrt(2) / 2), as indicated in Figure 83. Note that the approximate coordinates, accurate to 2 significant figures, are the values we used previously for this angle so that the approximate coordinates are (.71, .71).

Self-critique (if necessary):
Self-critique Rating:
Question: `q008. Sketch the triangle corresponding to the angular position pi/3. Explain why this triangle is similar to the triangle you constructed for angular position pi/6. What therefore are the x and y coordinates of the theta = pi/3 point on the unit circle?
Your solution:
Confidence Assessment:
Given Solution:
`aThe triangle is shown in Figure 88. The horizontal and vertical sides are reversed from the pi/6 triangle. So the coordinates of the points are also reversed to give us (1/2, sqrt(3)/2).

Self-critique (if necessary):
Self-critique Rating:
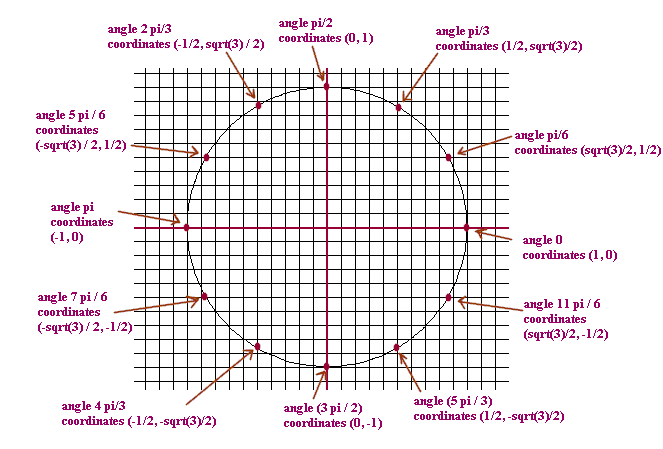
Question: `q009. Give the x and y coordinates of the points on the unit circle corresponding to angles which are multiples of pi/6. Sketch the unit circle and all angles which are multiples of pi/6, in give their coordinates.
Your solution:
Confidence Assessment:
Given Solution:
`aFigure 50 shows the angles 0, pi/6, pi/3, pi/2, 3 pi/2, 5 pi/6, ..., 2 pi with accurate values for the coordinates of the points.
Self-critique (if necessary):
Self-critique Rating:
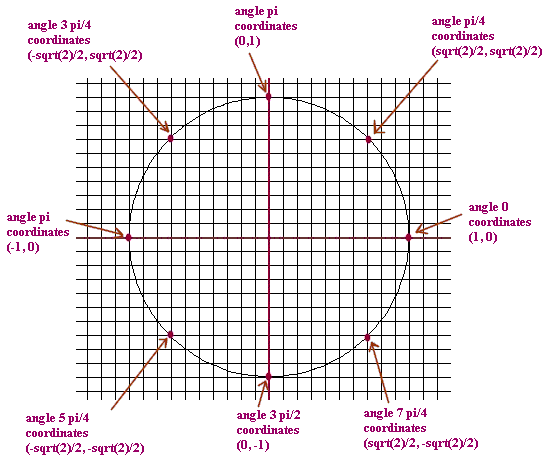
Question: `q010. Give the x and y coordinates of the points on the unit circle corresponding to angles which are multiples of pi/4. Sketch the unit circle and all angles which are multiples of pi/6, in give their coordinates.
Your solution:
Confidence Assessment:
Given Solution:
`aFigure 28 shows the angles 0, pi/4, pi/2, 3 pi/4, 2 pi, 5 pi/4, ..., 2 pi with accurate values for the coordinates of the points.
Self-critique (if necessary):
Self-critique Rating:
Question: `q011. Make the table for sin(theta) vs. theta with 0 <= theta < 2 pi, using an increment of pi/4. Sketch the corresponding graph. Now reverse the columns of the table and sketch the associated graph. Does your first graph represent a function? Does your second graph represent a function?
Your solution:
Confidence Assessment:
Given Solution:
`aUsing .71 to stand for sqrt(2) / 2 (your table should use sqrt(2)/2 where this one uses .71) we have the following table:
theta sin(theta)
0 0.0
pi/4 0.71
pi/2 1.0
3 pi/4 0.71
pi 0.0
5 pi/4 -0.71
3 pi/2 -1.0
7 pi/4 -0.71
2 pi 0.0.
The reversed table is
sin(theta) theta
0.0 0
0.71 pi/4
1.0 pi/2
0.71 3 pi/4
0.0 pi
-0.71 5 pi/4
-1.0 3 pi/2
-0.71 7 pi/4
0.0 2 pi.
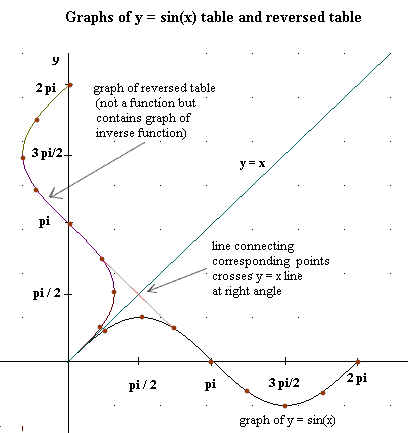
The corresponding graphs are indicated in figure 68. The red dots indicate points on the table; the rest of the function is filled in from what we know about the shape of the graph of y = sin(x).
The graph of the sine function is the usual graph. The graph of the reversed column doesn't represent a function because for example the horizontal coordinate zero is associated with two different values, 0 and pi (and also 2 pi). Another way of saying this is that the function fails the vertical line test, which says that a graph can represent a function only if any vertical line intersecting the graph of the function intersects the graph in only 1 point. Still another way of saying the same thing is that any function must be single-valued, with any number you put into the function giving you exactly 1 value.
For most numbers the first column of the inverted table we get 2 values. The numbers in the first column usually appear twice. For example sqrt(2)/2 in the first column is listed next to pi/4 and also next to 3 pi/4, 0 is listed with 0 and also with pi, etc..
Self-critique (if necessary):
Self-critique Rating:
Question: `q012. Now restrict the original table of sin(theta) vs. theta to values of theta for which pi/2 <= theta <= 3 pi/2, then reverse columns of the table. Does the resulting table give you a function? Sketch the graph corresponding to the table.
Your solution:
Confidence Assessment:
Given Solution:
`aThe table is as follows
theta sin(theta)
pi/2 1.0
3 pi/4 0.71
pi 0.0
5 pi/4 -0.71
3 pi/2 -1.0
The inverted table is as follows: sin(theta) theta
1.0 pi/2
0.71 3 pi/4
1.0 pi
-0.71 5 pi/4
-1.0 3 pi/2
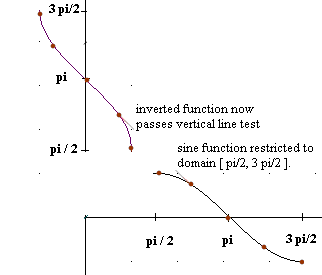
Each number in the first column appears exactly once in the table for the inverted function. The corresponding graphs are shown in figure 14. We see that the sine-function graph passes a horizontal line test, so that the inverted function passes a vertical-line test. Any vertical line passing through the inverted graph passes through at exactly point, showing that the graph does define a function.
Self-critique (if necessary):
Self-critique Rating:
Question: `q013. If we make a table of sin(theta) vs. theta for -pi/2 <= theta <= pi/2, can this table be inverted to give us a function?
Your solution:
Confidence Assessment:
Given Solution:
`aThe inverted table is as follows:
The table for the sine function is as follows
theta sin(theta)
-pi/2 0
-pi/4 -0.71
0 0
pi/4 0.71
pi/2 1.0
The inverted table is as follows:
sin(theta) theta
-1.0 -pi/2
-.71 -pi/4
0.0 0
0.71 pi/4
1.0 pi/2
Each number in the first column appears exactly once. The corresponding graph is shown in figure 34. Any vertical line passing through the graph passes through at exactly point, showing that the graph does define a function.
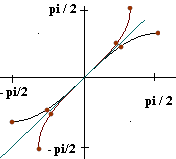
Self-critique (if necessary):
Self-critique Rating:
Question: `q014. Either of the functions graphed in the previous two exercises constitute inverses of portions of the sine function. Re-label the last table you made (the inverted table), labeling the first column x and the second column arcsin(x). This function is the generally accepted inverse of the sine function. What are the values of arcsine (.71), arcsine (0) and arcsin(-1)?
Your solution:
Confidence Assessment:
Given Solution:
`aThe table is as follows: sin(theta) theta
-1.0 -pi/2
-.71 -pi/4
0.0 0
0.71 pi/4
1.0 pi/2
Arcsine(.71) is the number in the second column of the table across from .71 in the first column. This number is pi/4.
Arcsine(0) is the number in the second column of the table across from 0 in the first column. This number is 0.
Arcsine(-1) is the number in the second column of the table across from 1 in the first column. This number is -pi/2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q015. What are the solutions to the following equations:
arcsin(x) = pi/4;
arcsin(x) = -pi/3;
sin(x) = 1.
Your solution:
Confidence Assessment:
Given Solution:
`aIf arcsin(x) = pi/4 then x appears next to pi/4 on the table of sin(x) vs. x. In other words sin(pi/4) = x. Since sin(pi/4) = sqrt(2)/2 we have x = sqrt(2)/2.
Another way of putting this is to say arcsin(sqrt(2)/2) = pi/4.
If arcsin(x) = -pi/3, similarly, this means that x = sin(-pi/3) so that x = -sqrt(3) / 2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q016. Find solutions to the following equations:
sin(2x) = .87;
sin(3x/4 + pi) = -.5?
Your solution:
Confidence Assessment:
Given Solution:
`aStarting with sin(2x) = .87, apply the arcsin function to both sides of the equation. We get the equation
arcsin ( sin(2x) ) = arcsin(.87).
The arcsin and the sine function are inverse functions; one 'undoes' the other so that arcsin(sin(2x)) = 2x. So we obtain
2x = arcsin(.87).
We know from the table of the sine function that arcsin(.87) = pi/3 so we have
2x = pi/3.
We divide both sides by 2 to obtain
x = pi/6.
Using a similar strategy for the second equation we write
arcsin( sin(3x/4) + pi) = arcsin(-.5), which gives us
3x/4 + pi = -pi/6 so that
3x / 4 = -pi/6 - pi = -7pi/6
x = 4/3(- 7 pi/6) = -28 pi / 18 = -14 pi / 7.
Self-critique (if necessary):
Self-critique Rating:
Question: `q017. Find solutions to the following equations:
sin(3x) = .38;
sin(2x+pi/4) = .93.
Your solution:
Confidence Assessment:
Given Solution:
`aIf sin(3x) = .38 then we have
arcsin( sin(3x) ) = arcsin(.38).
.38 doesn't appear on any of our tables so we have to find arcsin(.38) using a calculator. The arcsin key is sometimes labelled arcsin, sometimes sin^-1, and is often the 2d function on the sine key. We find that arcsin(.38) is about .39. So we have
3x = .39, so that
[]x = .39 / 3 = .13.
If sin(2x+pi/4) = .93 then
arcsin(2x + pi/4) = arcsin(.93). Using the calculator to find arcsin(.93) we get
2x + pi/4 = 1.19, approx..
We easily solve for x to obtain
x = (1.19 - pi/4) / 2 = .2 approx.
Self-critique (if necessary):
Self-critique Rating:
Question: `q018. For what values of t do we have sin(t + pi/3) equal to .5? Give the values for which t + pi/3 lies between 0 and 2 pi.
Are there values of t for which t + pi/3 lies outside the interval from 0 to 2 pi?
Your solution:
Confidence Assessment:
Given Solution:
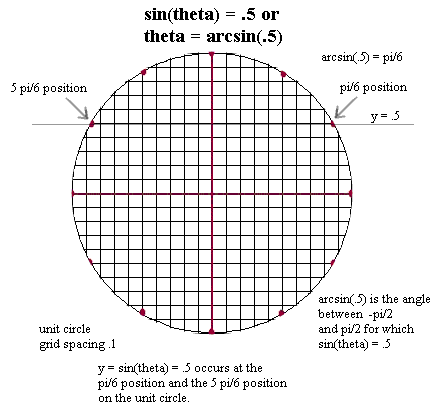
`asin(t+pi/3) = .5 means that sin(theta) = .5, with theta = t + pi/3.
The reference-circle picture of sin(theta) = .5 is given in Figure 60. We see that this occurs at the angle arcsin(.5) = pi/6 as well as at 5 pi/6.
So sin(t + pi/3) = .5 for t + pi/3 = pi/6 and for t + pi/3 = 5 pi/6. We can solve each of these equations for t:
t + pi/3 = pi/6 is solved by adding -pi/3 to both sides to obtain t = - pi/6.
t + pi/3 = 5 pi/6 is similarly solved to get t = pi.
Any angle which is coterminal with either theta = pi/6 or with 5 pi/6 (e.g., pi/6 + 2 pi, pi /6 + 4 pi, pi/6 + 6 pi, etc. or 5 pi/6 + 2 pi, 5 pi/6 + 4 pi, etc. ) will yield the same y coordinate and therefore the same value of the sine.
STUDENT QUESTION: I still don't
really understand the concept of t . I used the notes
from the last qa and I am still having trouble making sense
of it.
INSTRUCTOR RESPONSE:
Theta is the reference-circle angle.
t is the variable that determines the reference-circle angle,
but t is not itself an angle.
The given solution starts with the following two lines:
sin(t+pi/3) = .5 means that sin(theta) = .5, with theta = t + pi/3.
The reference-circle picture of sin(theta) = .5 is given in Figure 60. We see that this occurs at the angle arcsin(.5) = pi/6
as well as at 5 pi/6.
Once you understand these statements the rest follows fairly easily. If my first note doesn't help, can you tell me specifically what you do and do not understand about these statements?
Self-critique (if necessary):
Self-critique Rating:
Question: `q019. What are the first four positive values of t for which sin(t + pi/3) = .5?
Your solution:
Confidence Assessment:
Given Solution:
`aAs seen in the preceding problem sin(t + pi/3) = .5 when t + pi/3 = pi/6, 5 pi/6, pi/6 + 2 pi, 5 pi/6 + 2 pi, pi/6 + 4 pi 5 pi/6 + 4 pi, etc.. We also saw that the first two solutions, corresponding to theta = pi/6 and theta = 5 pi/6, are t = -pi/6 and t = pi. Only the second of these solutions is positive.
The solutions corresponding to theta = t + pi/3 = pi/6 + 2 pi, 5 pi/6 + 2 pi, pi/6 + 4 pi, 5 pi/6 + 4 pi, etc., will also be positive. Setting t + pi/3 equal to each of these angles and solving for t we obtain solutions
t = 11 pi / 6,
t = 5 pi/2,
t = 25 pi/6,
t = 9 pi/2.
The first four positive solutions are t = pi/2, 11 pi/6, 5 pi/2, 25 pi/6.
Complete Assignment 5, including Class Notes, text problems and Web-based problems as specified on the Assts page.
When you have completed the entire assignment run the Query program. Submit SEND files from Query and q_a_.