011. Conic sections
Question: `q001. What is the distance from (3, 5) to (7, 2)?
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance is the hypotenuse of a right triangle with vertices at the two points, whose legs are parallel to the x and y axes and whose hypotenuse runs from one point to the other.
The legs of the triangle are thus 7 - 3 = 4 and 2 - 5 = -3, and the hypotenuse is sqrt(4^2 + (-3)^2) = sqrt(25) = 5.
Self-critique (if necessary):
Self-critique Rating:
Question: `q002. What is the distance from (7, 2) to (x, y)?
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance is the hypotenuse of a right triangle with vertices at the two points, whose legs are parallel to the x and y axes and whose hypotenuse runs from one point to the other.
The legs of the triangle are thus x - 7 and y - 2, and the hypotenuse is sqrt((x-7)^2 + (y-2)^2).
Self-critique (if necessary):
Self-critique Rating:
Question: `q003. What is the distance from (x1, y1) to (x, y)?
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance is the hypotenuse of a right triangle with vertices at the two points, whose legs are parallel to the x and y axes and whose hypotenuse runs from one point to the other.
The legs of the triangle are thus x - x1 and y - y1, and the hypotenuse is sqrt((x-x1)^2 + (y-y1)^2).
Self-critique (if necessary):
Self-critique Rating:
Question: `q004. What is the distance from (x1, y1) to (x2, y2)?
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance is the hypotenuse of a right triangle with vertices at the two points, whose legs are parallel to the x and y axes and whose hypotenuse runs from one point to the other.
The legs of the triangle are thus x2 - x1 and y2 - y1, and the hypotenuse is sqrt((x2-x1)^2 + (yy-21)^2).
Self-critique (if necessary):
Self-critique Rating:
Question: `q005. Write as an equation: The distance from (7, 2) to (x, y) is 9.
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance from (7, 2) to (x, y) is sqrt((x-7)^2 + (y-2)^2), so the statement says that sqrt((x-7)^2 + (y-2)^2) = 9. Note that both sides of this equation could be squared to get (x-7)^2 + (y-2)^2 = 81.
Self-critique (if necessary):
Self-critique Rating:
Question: `q006. Write as a system of two equations: The distance from (7, 2) to (x, y) is 9 and distance from (4, 1) to (x, y) is 10. Solve the system for x and y.
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance from (7, 2) to (x, y) is sqrt((x-7)^2 + (y-2)^2), so the first statement says that sqrt((x-7)^2 + (y-2)^2) = 9.
The distance from (4, 1) to (x, y) is sqrt((x-4)^2 + (1-y)^2), so the second statement says that sqrt((x-4)^2 + (1-y)^2) = 10.{}
If we square both equations we get (x-7)^2 + (y-2)^2 = 81 and (x-4)^2 + (1-y)^2 = 100.
Expanding the squares in these equations we get
x^2 - 14 x + 49 + y^2 - 4 y + 4 = 81 and
x^2 - 8 x + 16 + y^2 - 2 y + 1 = 100.
Collecting terms we have{}
x^2 - 14 x + y^2 - 4 y = 28 and
x^2 - 8 x + y^2 - 2 y = 83.
Subtracting the second equation from the first we get
-6x - 2 y = -55, which we solve for y to get
y = -3x + 55/2.
Substituting this expression into the first equation we get
{}x^2 - 14 x + 49 + (-3x + 55/2)^2 - 4 ( -3x + 55/2 ) + 4 = 81, which we expand to get
10·x^2 - 167·x + 701.25 = 83.
Solving for x (using the quadratic formula) we get two solutions, x = 11.16 and x = 5.54.
Substituting these x values into the second equation we get y^2 - 2·y + 35.2656 = 83, with solution y = 7.98 or y = -5.98; and y^2 - 2·y - 34071/2500 = 83 with solutions y = 10.88 and y = -8.88. This gives us possible solutions (11.16, 7.98), (11.16,-5.98), (5.54, 10.88) and (5.54, -8.88).
{}Checking out these solutions with the first equation we see that (11.16, -5.98) and (5.54, 10.88) are in fact solutions, while (11.16, 7.98) and (5.54, 10.88) are not.
Self-critique (if necessary):
Self-critique Rating:
Question: `q007. Write as an equation: The distance from (7, 2) to (x, y) is equal to the distance from (4, 1) to (x, y). Simplify this equation.
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance from (7, 2) to (x, y) is sqrt((x-7)^2 + (y-2)^2), and the distance from (4, 1) to (x, y) is sqrt((x-4)^2 + (1-y)^2). To say that these distances are equal is to say that
sqrt((x-7)^2 + (y-2)^2)= sqrt((x-4)^2 + (1-y)^2)
Squaring both sides we get (x-7)^2 + (y-2)^2 = (x-4)^2 + (1-y)^2.
Expanding the squares we
x^2 - 14 x + 49 + y^2 - 4 y + 4 = x^2 - 8 x + 16 + y^2 - 2 y + 1.
Subtracting x^2 - 8 x + 16 + y^2 - 2 y + 1 from both sides we get
-6x - 2y + 36 = 0.
Solving for y we get
y = -3x + 18.
This is a linear equation, telling us that the set of points (x, y) which are equidistant from (7, 2) and (4, 1) lie along a straight line with slope -3 and y-intercept 18.
Recall from basic geometry that the perpendicular bisector of a line segment through two points is the line which is equidistant from those points. Since the slope of the segment from (7,2) to (4,1) is 1/3, we expect that the perpendicular bisector will have slope - 1 / (1/3) = -3, as is the case for the line we have obtained. It is also easy to verify that the line y = -3x + 18 contains the midpoint between (7, 2) and (4, 1): The midpoint is ( (7+4)/2, (2+1)/2 ) = (11/2, 3/2). Substitution will show that this point lies on the line y = -3x + 18.
Self-critique (if necessary):
Self-critique Rating:
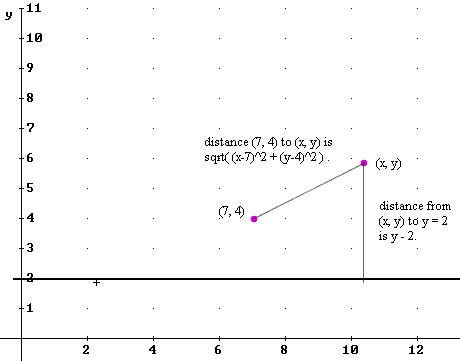
Question: `q008. Write as an equation: The distance from ((7, 4) to (x, y) is equal to the distance from the line y = 2 to (x, y). Simplify this equation.
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance from (7, 4) to (x, y) is sqrt( (x-7)^2 + (y-4)^2 ). The distance from (x, y) to the line y = 2 lies along the vertical line from (x, y) to y = 2; it is clear from Figure 49 that this distance is | y - 2 |.
Thus we have sqrt( (x-7)^2 + (y-4)^2 ) = y - 2. Squaring both sides we get
(x-7)^2 + (y-4)^2 = (y - 2 ) ^ 2. Expanding the squares we have
x^2 - 14 x + 49 + y^2 - 8 y + 16 = y^2 - 4 y + 4. Subtracting y&2 - 4 y + 4 from both sides we have
x^2 - 14 x + 49 - 4 y + 12 = 0.
You aren't expected to have known the rest of this solution before, but you need to note the following:
Note that this equation is quadratic in x and linear in y. An equation of this form is generally rearranged into the form (y - k) = A * (x - h) ^ 2. In this case we can add 4y - 12 to both sides to get
x^2 - 14 x + 49 = 4 ( y - 3). This simplifies to
(y - 3) = 1/4 ( x - 7)^2.

Self-critique (if necessary):
Self-critique Rating:
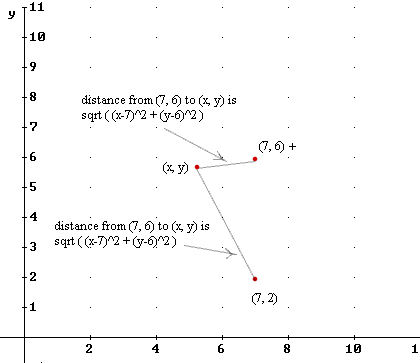
Question: `q009. Write as an equation: The distance from (7, 6) to (x, y) plus the distance from (7, 2) to (x, y) is 6. Simplify this equation.
Your solution:
Confidence Assessment:
Given Solution:
`aA sketch of the points (7, 2) and (7, 6), with a possible point (x,y) satisfying the description is shown in Figure 5.
The distance from (x, y) to (7, 6) is (sqrt((x-7)^2 + (y-6)^2) and the distance from (x, y) to (7, 2) is sqrt((x-7)^2 + (y-2)^2). To say that the sum of these distances is 6 is to say that
sqrt((x-7)^2 + (y-6)^2) + sqrt((x-7)^2 +(y-2)^2) = 6.
This equation is a bit messy to simplify. If we first square both sides we get
((x-7)^2 + (y-6)^2) + 2 sqrt [((x-7)^2 + (y-6)^2) * ((x-7)^2 +(y-2)^2)] + ((x-7)^2 +(y-2)^2) = 36.
We still have a square root in our equation so we rearrange the equation so that the square root is isolated on one side:
2 sqrt [((x-7)^2 + (y-6)^2) * ((x-7)^2 +(y-2)^2)] = 36 - ((x-7)^2 + (y-6)^2) - ((x-7)^2 +(y-2)^2)
If we square both sides and are fortunate enough to keep all the variables straight we get
4·x^4 - 112·x^3 + 8·x^2·y^2 - 64·x^2·y + 1336·x^2 - 112·x·y^2 + 896·x·y - 7728·x + 4·y^4 - 64·y^3 + 744·y^2 - 3904·y + 18020 = 4·x^4 - 112·x^3 + 8·x^2·y^2 - 64·x^2·y + 1192·x^2 - 112·x·y^2 + 896·x·y - 5712·x + 4·y^4 - 64·y^3 + 664·y^2 - 3264·y + 10404,
which looks pretty bad until we notice that the x^4, y^4, x^3, y^2, x^2 y^2, x^2 y, x y^2 and xy terms are the same on both sides so that if we simply subtract the entire right-hand side from both sides and the divide both sides by 16 we get
9·x^2 - 126·x + 5·y^2 - 40·y + 476 = 0.
Note that this equation is quadratic in both x and y. An equation of this form does not always have real solutions, but when it does the graphed solution points will lie on either an ellipse or a hyperbola.
Self-critique (if necessary):
Self-critique Rating:
Question: `q010. Write as an equation: The distance from (x, y) to (7, 6) is 6 units greater than the distance from (x, y) to (7, 2). Do not simplify this equation.
Your solution:
Confidence Assessment:
Given Solution:
`aThe distance from (x, y) to (7, 6) is sqrt((x-7)^2 + (y-6)^2) and the distance from (x, y) to (7, 2) is sqrt((x-7)^2 + (y-2)^2). To say that the first is 6 units greater than the second is to say that
sqrt((x-7)^2 + (y-6)^2) - sqrt((x-7)^2 +(y-2)^2) = 6.
This equation will end up being quadratic, as was the equation in the preceding exercise.
Self-critique (if necessary):
Self-critique Rating:
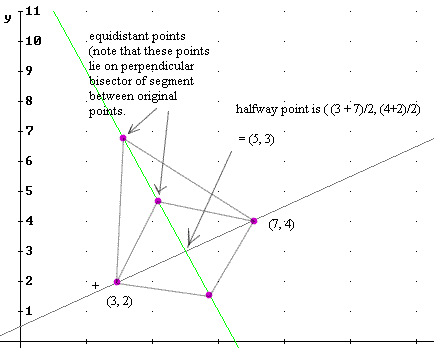
Question: `q011. Sketch the points (7, 4) and (3, 2) on a set of coordinate axes. Locate the point halfway between these two points. Then locate three more points which lie at equal distances from the two points, but not on the line joining the two points.
Your solution:
Confidence Assessment:
Given Solution:
`aThis situation is depicted in Figure 22. The halfway point is found by simply averaging the x coordinates and averaging the coordinates: we get
midway point: ( (7 + 3) / 2, (4 + 2) / 2) = (5, 3).
Three other points are depicted, each showing the two equal segments (one from each of the original points to the equidistan point) which show that the points are equidistant.
It is worth noting that these equidistant points all lie on the perpedicular bisector of the segment joining the two original points. You should be aware of how this is proved in terms of similar triangles which turn out to be right triangles.
Self-critique (if necessary):
Self-critique Rating:
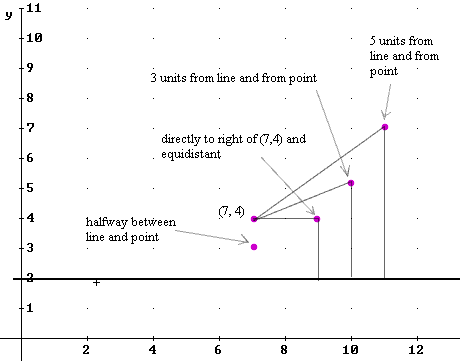
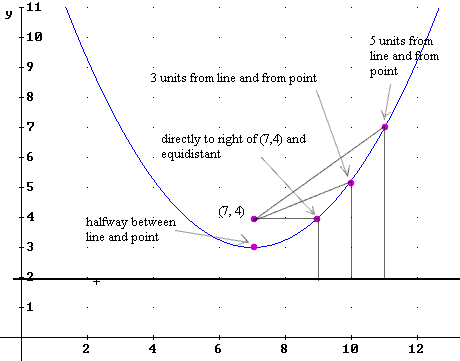
Question: `q012. Sketch the point (7, 4) on a set of coordinate axes, and also sketch the line y = 2 on the same set of axes. Sketch the point which lies halfway between the point and the line. Then locate a point which lies directly to the right of (7,4) which is at the same distance from (7,4) as from the line y = 2. Approximately locate also the points which are located as follows:
3 units above the line and also 3 units away from (7, 4)
4 units above the line and also 4 units away from (7, 4)
5 units above the line and also 5 units away from (7, 4).
Your solution:
Confidence Assessment:
Given Solution:
`aFigure 95 depicts the horizontal line y = 2 and the point (7, 4).
The point halfway between (7, 4) and the line y = 2 is indicated; note that this point lies at (7, 3).
Moving directly to the right of (7, 4) we encounter the indicated point directly to its right and equidistant from (7, 4) and the line y = 2. Note that the horizontal and vertical line segments from this point indicate these equal distances.
We also see the points which lie 3 units from both (7,4) and the line y = 2, and 5 units from line and point; note for each of these points that the line segment to the point (7,4) is the same length as the segment directed to the y = 2 line.
Self-critique (if necessary):
Self-critique Rating:
Question: `q013. Sketch the set of points (x, y) you think would satisfy the condition that the distance from (x, y) to (7, 4) is equal to the distance from the line y = 2.
Your solution:
Confidence Assessment:
Given Solution:
`aIn figure 15 we see the curve that passes through the indicated points, and which satisfies the given condition. Every point on this curve is equidistant from (7, 4) and from the line y = 2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q014. Sketch the points (7, 6) and (7, 2) on a set of coordinate axes.
How far is the point (7, 7) from each of these points? What is the sum of these distances?
What other point gives the same sum?
Your solution:
Confidence Assessment:
Given Solution:
`a(7,7) lies directly above (7,6), at a distance of 1 unit. (7,7) lies exactly 5 units above (7,2). So the sum of the two distances is 1 + 5 = 6 units.
The point (7, 1), lying 1 unit directly below (7,2), also has the characteristic that the sum of the two distances is 6.
Self-critique (if necessary):
Self-critique Rating:
Question: `q015. We saw in the preceding exercise that (7, 7) lies at distance 1 from (7, 6) and at distance 5 from (7, 2), so that the sum of these distances is 6. What is the sum of the distances from (8, 4) to (7, 6) and to (7, 2)? What is the sum of the distances from (9, 4) to these points? What is the sum of the distances from (10, 4) to these points? Estimate the x coordinate that makes the sum of the distances from (x, 4) to (7, 6) and to (7, 2) equal to 6. If you can find the exact x coordinate required.
Your solution:
Confidence Assessment:
Given Solution:
`aIn Figure 64 we see the indicated points. The figure shows that the points (8,4), (8,5) and (8,6) lie at increasing distances from (7,6) and from (7,2).
The distance from (7,6) to (8,4) is sqrt( (8-7)^2 + (4-6)^2) = sqrt(1+4) = sqrt(5); the distance from (7,2) to (8,4) is also sqrt(5). So the sum of the two distances is 2 sqrt(5) = 4.46 approx., which is less than 6.
The distance from (7,6) to (9,4) is sqrt( (9-7)^2 + (4-6)^2) = sqrt(4 + 4) = sqrt(8); the distance from (7,2) to (8,4) is also sqrt(8). So the sum of the two distances is 2 sqrt(8) = 5.56 approx., which is still less than 6.
From the pattern of the preceding two points it should be clear that the sum of distances for the point (10,4) will exceed 6. To verify this we calculate the distance from (7,6) to (10,4) and see that the distance is sqrt(13), as is the distance from (7,2) to (10,4). Thus the sum of distances is 2 sqrt(13) = 7.2, approx., which does indeed exceed 6.

Self-critique (if necessary):
Self-critique Rating:
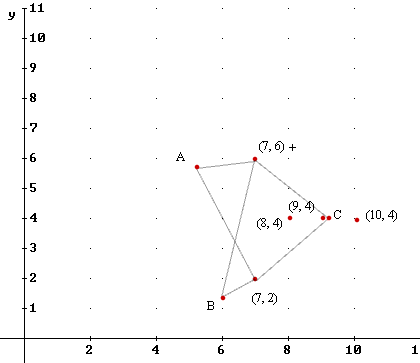
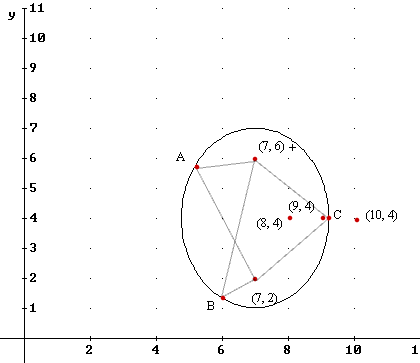
Question: `q016. Sketch the set of all points (x, y) you think would satisfy the condition that the sum of the distances from (x, y) to (7, 6) and to (7, 2) is 6.
Your solution:
Confidence Assessment:
Given Solution:
`aOne such point will lie between (9,4) and (10,4); from the pattern of results in the preceding problem we expect that this point will lie much closer to (9,4) than to (10,4). Figure 29 shows the point C, as described. Points A and B also have the property that the sum of the distances to (7,6) and (7,2) is equal to 6.
Figure 87 shows all these points with the curve every point of which whose property is the same as that of C, A and B. That is, for every point of this curve the sum of the distances from that point to (9,4) and to (10,4) is 6.
Self-critique (if necessary):
Self-critique Rating: