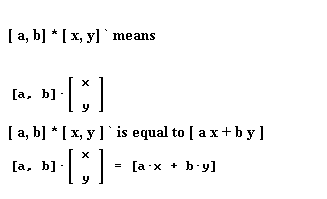
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
013. Some Stochastic Matrices; Interpretation of Matrices, Multiplication of Matrices.
Question: `q001. If an island has a population of 1000 individuals, 500 of whom are sane and the rest of whom are demented, and if at the end of each year 10% of those who were sane at the beginning of the year are demented at the end, while 20% of those who are demented at the beginning of the year are sane, then how many sane and how many demented will there be at the end of each of the first three years?
Your solution:
Confidence Assessment:
Given Solution:
`aDuring the first year 10% of the 500 sane will become demented and 20% of the 500 demented will become sane. Thus 50 sane become demented and 100 demented become sane. The sane population will therefore lose 50 but gain 100 and end up at 550, while the demented population will lose 100 and gain 50, ending up at 450.
During the second year 10% of the 550 sane will become demented and 20% of the 450 demented will become sane. Thus 55 sane become demented and 90 demented become sane. The sane population will therefore lose 55 but gain 90 and end up at 585, while the demented population will lose 90 and gain 55, ending up at 415.
During the third year 10% of the 585 sane will become demented and 20% of the 415 demented will become sane. Thus 58.5 sane become demented and 83 demented become sane. The sane population will therefore lose 59.5 but gain 83 and end up at 609.5, while the demented population will lose 83 and gain 58.5, ending up at 390.5.
Self-critique (if necessary):
Self-critique Rating:
Question: `q002. Given the transition percents from the preceding problem, if there are S sane individuals and D demented at the beginning of a year, what expression represents the numbers S' of sane and D' of demented at the end of the year?
Your solution:
Confidence Assessment:
Given Solution:
`aDuring the year 10% of the S sane will become demented and 20% of the D demented will become sane. Thus .1 S sane become demented and .2 D demented become sane. The sane population will therefore lose .1 S but gain .2 D and end up at S' = S - .1 S + .2 D, while the demented population will lose .2 D and gain .1 S, ending up at D' = D - .2 D + .1 S.
We can simplify these expressions for S' and D', obtaining S' = .9 S + .2 D and D' = .1 S + .8 D.
Self-critique (if necessary):
Self-critique Rating:
Question: `q003. The expression [ a b ] consists of the two numbers a and b in a row, set off by brackets. The expression [ x y ]` consists of the two numbers x and y written in a column and set of by brackets, as indicated in Figure 32. The ` designates the 'transpose operator' which transposes rows into columns and columns into rows.
The product [ a b ] [ x y ]` is written as indicated in Figure 32, and is equal to the single number which you get by calculating a * x + b * y.
What do you get from the product [ .1 .8 ] [ 550 450 ]` and what does this result have to do with the Sane-Demented problem?
Your solution:
Confidence Assessment:
Given Solution:
`aSince [ a b ] [ x y ]` = a * x + b * y, the product [ .1 .8 ] [ 550 450 ]` will be
[ .1 .8 ] [ 550 450 ]` = .1 * 550 + .8 * 450 = 55 + 360 = 415.
This calculation is shown in Figure 27.
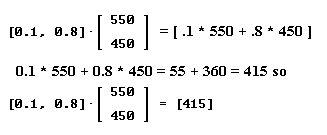
Self-critique (if necessary):
Self-critique Rating:
Question: `q004. Write an expression of the form [ a b ] [ x y ]` which represents the number of sane people 1 year after the populations were s and d. Assume the same transition percents as before.
Your solution:
Confidence Assessment:
Given Solution:
`aWe saw previously that s' = .9 s + .2 d, which can be taken as representing the fact that 90% of the sane remain sane while 20% of the demented become sane. To get the expression .9 s + .2 d we can multiply [ .9 .2 ] [ s d ], as shown in Figure 70.

Self-critique (if necessary):
Self-critique Rating:
Question: `q005. Write an expression of the form [ a b ] [ x y ]` which represents the number of demented people a year after the populations were s and d. Assume the same transition percents as before.
Your solution:
Confidence Assessment:
Given Solution:
`aWe saw previously that d' = .1 s + .8 d, which can be taken as representing the fact that 80% of the demented remain demented while 10% of the sane become demented. To get the expression .1 s + .8 d we can multiply [ .1 .8 ] [ s d ], as shown in Figure 4.
The row matrix [ .1 .8 ] is said to represent the transition rule for the demented population, while the row matrix [ .9 .2 ] of the previous exercise is said to represent the transition rule for the sane population.
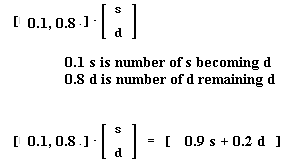
Self-critique (if necessary):
Self-critique Rating:
Question: `q006. The expression [ [ a b], [ c d ] ] is called a matrix, and consists of the two rows [ a b ] and [ c d ] enclosed in a large bracket, as indicated in Figure 89. What is the matrix whose first row represents the transition in the number of sane people, and whose second row represents the transition in the number of demented people?

Your solution:
Confidence Assessment:
Given Solution:
`aThe two rows, as seen in previous problems, are [ .9 .2 ] and [ .1 .8]. The matrix is thereefore [ [ .9 .2 ], [ .1 .8 ] ]. This matrix is depicted in Figure 94.
Self-critique (if necessary):
Self-critique Rating:
Question: `q007. The product of the expression [ [ a b], [ c d ] ] and [ x y ]` is the column vector [ a x + b y c x + d y]`, as illustrated in Figure 10. Note how the first row of the product matrix is the product of the row [ a b] and column [ x y ]` while the second row of the product matrix is the product of the row [ c d ] and the column [ x y ]`.
Describe the result of the multiplication [ [ .9 .2 ], [ .1 .8 ] ] * [ 585 415 ]` and give the meaning of your result.
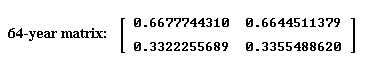
Your solution:
Confidence Assessment:
Given Solution:
`aFigure 90 shows the result of the matrix multiplication [ [ .9 .2 ], [ .1 .8 ] ] * [ 585 415 ]`. Below this result is the result of multiplying the first row, then the second, by the column vector [ 585 415 ]`.
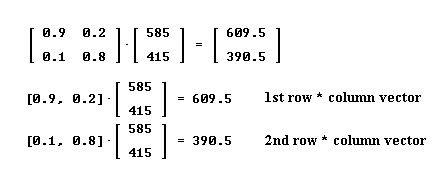
Your solution:
Confidence Assessment:
Given Solution:
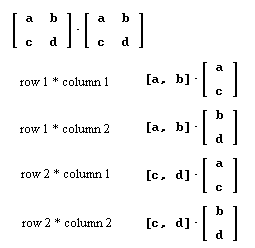
`aq008. To multiply the matrix [ [ a b], [ c d ] ] by itself we note that the product [ [ a b], [ c d ] ] * [ [ a b], [ c d ] ], written as indicated in Figure 104, can be seen as a matrix with two rows (the leftmost matrix, with the rows 'boxed' and labeled row 1 and row 2), and a matrix with two columns (the rightmost matrix, with the columns 'boxed' and labeled column 1 and column 2).
As has been done in every multiplication so far, in any multiplication we can only multiply a row on the left by a column on the right.
Let [ [ a b], [ c d ] ] stand for the matrix of transitions for the sane-demented problem. For each possible combination of a row on the left and a column on the right, multiply the row by the column. Give your results.
Your solution:
Confidence Assessment:
Given Solution:
`aThe four possible combinations of row and column are depicted in Figure 117. To multiply [ [ .9 .2 ], [ .1 .8 ] ] * [ [ .9 .2 ], [ .1 .8 ] ] we multiply each row of the first matrix by each column of the second.
The first row and first column give us [ .9 .2 ] * [ .9 .1]`, resulting in solution .9 * .9 + .2 * .1 = .83.
The first row and second column give us [ .9 .2 ] * [ .2 .8]`, resulting in solution .9 * .2 + .2 * .8 = .34.
The second row and first column give us [ .1 .8 ] * [ .9 .1]`, resulting in solution .1 * .9 + .8 * .1 = .17.
The second row and second column give us [ .1 .8 ] * [ .2 .8]`, resulting in solution .1 * .2 + .8 * .8 = .64.
Self-critique (if necessary):
Self-critique Rating:
Question: `q009. The product [ [ a b], [ c d ] ] * [ [ a b], [ c d ] ] consists of a number for each row and column combination consisting of a row from of the first matrix and a column of the second. The number will be the product of the row and the column.
So we will have four numbers, one the product of the first row and the first column, one the product of the first row and the second column, one the product of the second row and the first column, and one the product of the second row and the second column. In the preceding problem we calculated these products for the sane-demented transition matrix.
These products are arranged in the product matrix, with the product of the first row and the first column in the first row and the first column of the product matrix, the product of the first row and the second column in the first row and the second column of the product matrix, the product of the second row and the first column in the second row and the first column of the product matrix, and the product of the second row and the second column in the second row and the second column of the product matrix.
What is the matrix we obtain when we multiply the transition matrix by itself?
Your solution:
Confidence Assessment:
Given Solution:
`aThe product of the first row and first column goes into the first row and first column of the product matrix.
The product of the first row and second column goes into the first row and second column of the product matrix.
The product of the second row and first column goes into the second row and first column of the product matrix.
The product of the second row and second column goes into the second row and second column of the product matrix, as shown in Figure 47.

Self-critique (if necessary):
Self-critique Rating:
Question: `q010. Multiplying the transition matrix by itself we obtained the matrix [ [.83 .34 ], [.17 .66 ] ].
What do we get if we multiply this matrix by the original population vector [ 500 500 ]`? What does this result have to do with the sane-demented problem?
Your solution:
Confidence Assessment:
Given Solution:
`aThe product of the matrix [ [.83 .34 ], [.17 .66 ] ] with the original population vector [ 500 500 ]` includes the product [ [.83 .34 ] [ 500 500 ]` = .83 * 500 + .34 * 500 = 415 + 170 = 585 and the product [.17 .66 ] [ 500 500 ]` = 85 + 330 = 415, arranged in the product vector [ 585 415 ] `.
This result contains the second-year sane and demented populations 585 and 415. The matrix [ [.83 .34 ], [.17 .66 ] ] obtained this result from the original populations, bypassing the 1-year populations.
Figure 44 shows the calculation of this result.
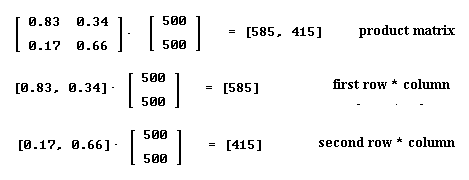
Self-critique (if necessary):
Self-critique Rating:
Question: `q011. If we multiply the 2-year transition matrix [ [.83 .34], [.17 .66] ] by itself, what matrix do we get and what is its meaning?
Your solution:
Confidence Assessment:
Given Solution:
`aTo obtain the product [ [.83 .34], [.17 .66] ] * [ [.83 .34], [.17 .66] ] we multiply each row of the first matrix by each column of the second. Figure 2 depicts the product. We have
first row * first column = [ .83 .34 ] [ .83 .17 ]` = .83 * .83 + .34 * .17 = .7467
first row * second column = [ .83 .34 ] [ .34 .66 ]` = .83 * .34 + .34 * .66 = .5066
second row * first column = [ .17 .66 ] [ .83 .17 ]` = .17 * .83 + .66 * .17 = .2533
second row * second column = [ .17 .66 ] [ .34 .66 ]` = .17 * .34 + .66 * .66 = .4934.
These results are inserted into the corresponding rows and columns to form the product matrix.
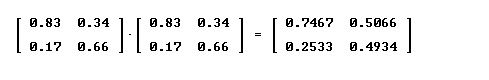
Self-critique (if necessary):
Self-critique Rating:
Question: `q012. If we multiply the 4-year matrix [ [.7467 .5066], [.2533 .4934] ] by itself what matrix do we get and what is the meaning of this matrix?
Your solution:
Confidence Assessment:
Given Solution:
`aThe result of the multiplication, shown in figure 7, is [ [ .68589 .62823 ], [ .31412 .37177 ] ], rounded to the 5th decimal place.
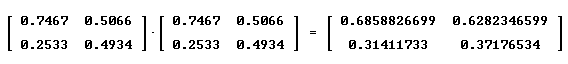
Self-critique (if necessary):
Self-critique Rating:
Question: `q013. If we multiply the 8-year matrix by itself we get the 16-year matrix. If we multiply this matrix by itself we get the 32-year matrix. Multiplying this matrix by itself we get the 64-year matrix, which is [ [.6677, .6644 ], [.3322, .3355 ] ].
What do we get if we multiply this matrix by the original population vector [ 500, 500 ]` and what is the significance of this result?
What do we get if we multiply the 64-year transition matrix by the population vector [ 900, 100 ]` and what is the significance of this result?
Your solution:
Confidence Assessment:
Given Solution:
`aThe 64-year matrix is depicted in Figure 10. Multiplying it by the population vector [500, 500] we get
[ [.6677, .6644 ], [.3322, .3355 ] ] * [500, 500]` = [666.05, 333.85]. This result tells us that after 64 years the population will consist of 666.05 Sand and 333.85 Demented--almost exactly double the number of Sand as Demented.
Multiplying the 64-year matrix by the population vector [900, 100] we get
[ [.6677, .6644 ], [.3322, .3355 ] ] * [900, 100]` = [667.37, 332.53], almost identical to the result we obtained for initial population vector [500, 500].
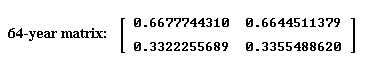
Your solution:
Confidence Assessment:
Given Solution:
`a&*&* another figure 10 ???? one labeled fig_10; same problem with fig_7 but no duplicate there
Self-critique (if necessary):
Self-critique Rating:
Question: `q014. Suppose that we have another island where there are three groups of people, sane, demented and borderline. Suppose that the number of sane who make the transition to demented is still 10% while the number of sane who make the transition to borderline is 15%, that the number of borderline who make the transition to sane is 15% while the number of borderline who make the transition to demented is 25%, that the number of demented who make the transition to sane is still 20% while the number of demented who make the transition to borderline is 15%.
Without setting up matrices yet, which group do you think will end up with the greatest and which with the least number of people after a large number of transitions?
Your solution:
Confidence Assessment:
Given Solution:
`aSorting the results out we see that the borderline group retains only 60% of its population in a transition, and gets only 15% from each of the other groups. The demented group retains 65% of its population and gets 10% from the Sane and 25% from the Borderline group, which would tend to indicate higher numbers except that if the Borderline group is the least populous there wouldn't be that many to draw from. The argument is similarly complicated for the Sane, who retain 75% of their population and gain 15% from Borderline and 20% from the Demented.
The conclusion remains unclear but based on the percentages retained a tentative prediction might be the Borderline would end up with the least and Sane with the most.
Self-critique (if necessary):
Self-critique Rating:
Question: `q015. What row vector would you multiply by the column vector [ S B D ]` in order to get the number of sane after a transition at the beginning of which the numbers of sane, demented and borderline are S, B and D?
What row vectors would you use to get the numbers of borderline and of demented from the same column vector?
What matrix would you multiply by the column vector [ S B D ]` in order to get the column vector [ S' B' D' ] of sane, demented and borderline after a transition?
Your solution:
Confidence Assessment:
Given Solution:
`aThe number of Sane after a transition is 75% of the number of Sane before transition, plus 15% of the number of Borderline, plus 20% of the number of Demented. So to get S' we would multiply [ .75 .15 .20 ] times the column vector [ S B D ] `.
{}The number of Borderline after a transition is 60% of the number of Borderline before transition, plus 15% of the number of Sane, plus 15% of the number of Demented. So to get B' we would multiply [ .15 .60 .15 ] times the column vector [ S B D ] `.
The number of Demented after a transition is 65% of the number of Demented before transition, plus 20% of the number of Sane, plus 15% of the number of Borderline. So to get D' we would multiply [ .20 .15 .65 ] times the column vector [ S B D ] `.
To get all three results at once we would multiply the matrix [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] times the column vector [ S B D ]`.
This solution is summarized in Figure 53.

Self-critique (if necessary):
Self-critique Rating:
Question: `q016. If you multiply the matrix [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ], which represents the transition in the preceding series of problems, by itself what matrix do you get and what does it represent?
Your solution:
Confidence Assessment:
Given Solution:
`aThe result is depicted in Figure 55. The product matrix is [ [ .605 .2525 .3025], [.2175 .42 .2175], [.1175 .3275 .48 ] ].
The product
[ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] * [ S B D ]` repesents the population at the end of the first year.
The product [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] * [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] * [ S B D ]` represents the population at the end of the second year.
Since matrix multiplication is associative the population at the end of the second year can also be expressed as the product [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] * [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] of the one-year transition matrix with itself, multiplied by the original population vector [ S B D ] `. Since this result gives the population at the end of the second year, the product
[ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] * [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] = [ [ .605 .2525 .3025], [.2175 .42 .2175], [.1175 .3275 .48 ] ]
represents a 2-year transition matrix.

Self-critique (if necessary):
Self-critique Rating:
Question: `q017. The matrix T = [ [ .75 .15 .10 ], [ .15 .60 .25 ], [ .20 .15 .65 ] ] represents the transition probabilities for the preceding series of problems, and as we just saw T^2 = [ [.605, .2525, .3025], [.2175, .42, .2175], [.1775, .3275, .40] ] represents the two-year transition matrix. As before if we multiply T^2 by itself we get T^4, which multiplied by itself gives us T^8, which multiplied by itself gives us T^16, which multiplied by itself gives us T^32, which multiplied by itself gives us T^64. T^64 = [ [.4479723274, .3817071874, .397645], [.2676946874, .2861475, .2676946874], [.284331875, .3321453124, .33466063124] ].
If we start with 500 sane, 300 demented and 200 borderline, what do we end up with after 64 transitions?
What if we had started with 1000 sane, 0 borderline and 0 demented?
What if we had started with 1000 borderline?
Your solution:
Confidence Assessment:
Given Solution:
`aT^64 * [ 500 300 200] ` = [ [.4479723274, .3817071874, .397645], [.2676946874, .2861475, .2676946874], [.284331875, .3321453124, .33466063124] ] * [ 500 300 200] ` = [ 418 273 309 ], with the numbers in the product matrix rounded to the nearest whole number.
The same product, only using the initial population vector [ 1000 0 0 ]`, gives us the same result, as is the case also with initial population vector [0 1000 0]`.
The powers of T converge as the power increases, just as the powers of the Sane-Demented transition matrix converged. Here the powers converge to [ [ .41..., .41, ..., .41... ], [.27..., .27..., .27...], [.31..., .31..., .31... ] ] and the populations converge to [ 414, 273, 313 ]`.
Figure 57 depicts the limiting matrix.
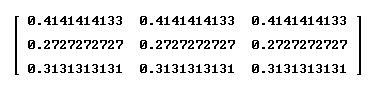
Self-critique (if necessary):
Self-critique Rating: