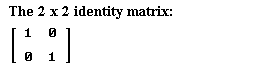
If your solution to stated problem does not match the given solution, you should self-critique per instructions at

   http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm

.

Your solution, attempt at solution.  If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it.  This response should be given, based on the work you did in completing the assignment, before you look at the given solution.

015.  Matrix Algebra; Solving the matrix equation A * X = C by finding the Inverse Matrix

Question:  `q001.  The equation a * x = c is solved by multiplying both sides by a^-1 to obtain a^-1 * a * x = a^-1 * c.  Since a^-1 * a = 1 we get 1 * x = a^-1 * c or just x = a^-1 * c.

Apply this method to the equation 3 x = 7.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q002.  In the preceding problem a^-1 is the number we multiply by a to get the identity 1.  In the specific example we had a = 3 so a^-1 = 1/3, with the result that a * a^-1 = 3 * 1/3 = 1.  The number 1 is the identity for multiplication.  It has the property that any number multiplied by 1 remains unchanged.  That's the idea of an identity.

For 2 x 2 matrices the identity is I = [  [1  0], [0  1] ], represented in Figure 63.  Show that if we multiply any 2 x 2 matrix [ [ a   b ] , [ c   d ] ] by I = [  [1  0], [0  1] ] that matrix remains unchanged.

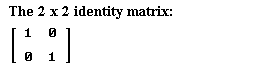
Your solution: 

Confidence Assessment:

Given Solution: 

`aMultiplying with the identity matrix on the left we have:

1st row * 1st column = [ 1   0 ] [ a  c ]` = a

1st row * 2nd column = [ 1  0 ] [ b  d ]` = b

2nd row * 1st column = [ 0  1 ] [ a  c ]` = c

2nd row * 2nd column = [ 0   1 ] [ b  d ]` = d

Placing these results in the appropriate positions in the product matrix we get the result indicated in the first equation of Figure 63.

Multiplying with the identity matrix on the right we have:

1st row * 1st column = [ a  b ] [ 1  0 ]` = a

1st row * 2nd column = [ a  b ] [ 0  1 ]` = b

2nd row * 1st column = [ c  d ] [ 1  0 ]` = c

2nd row * 2nd column = [ c   d ] [ 0  1 ]` = d.

Placing these results in the appropriate positions in the product matrix we get the result indicated in the second equation of Figure 63.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q003.  The inverse of a 2 x 2 matrix A is the matrix denoted by A^-1 which when multiplied by A gives the identity I = [  [1  0], [0  1] ].  It is tempting to conjecture that the inverse of the matrix  A = [ [ a  b ] , [ c    d ] ] is the matrix [ [ a^-1  b^-1 ] , [ c^-1   d^-1 ] ] = [ [ 1/a  1/b ] , [ 1/c   1/d ] ].  Show that this matrix is in fact not generally equal to the inverse of A = [ [ a  b ] , [ c   d ] ].

Your solution: 

Confidence Assessment:

Given Solution: 

`aIf [ [ 1/a  1/b ] , [ 1/c   1/d ] ] is the inverse matrix then [ [ 1/a  1/b ] , [ 1/c   1/d ] ] * [ [ a  b ] , [ c   d ] ] = [ [ 1  0 ], [0  1] ].  However, for example, the first row of the first matrix and the first column of the second matrix is [ 1/a   1/b] [ a  c ]` = 1 + c/b.  Unless c = 0, which cannot be assumed, this is not the first-row first-column element 1 of the identity matrix and this alone shows that the product matrix cannot be the identity [ [ 1  0 ], [0  1] ].

Figure 71 shows that the result of this multiplication is

[[ 1 + c/b,  d/b + b/a], [c/d + a/c, 1 + b/c] ],

which except in certain special cases is not equal to the identity matrix.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q004.  The way to get the inverse of a 2 x 2 matrix [ [ a  b ] , [ c    d ] ] is to start with the augmented matrix [ [ a  b | 1  0 ] , [ c    d | 0  1 ] ], which consists of the matrix [ [ a  b ] , [ c    d ] ]augmented by the identity matrix.  The augmented matrix is also pictured in Figure 76.

To get the inverse of A we add multiples of rows to rows and multiply rows by constant numbers to get the form [  [1  0 | *  * ], [0   1 | *  * ] ], where the asterisks * indicate the numbers that result from the process.  The matrix formed by these numbers is the inverse matrix we're looking for.

To obtain the inverse of the matrix [  [2  3], [-4  1] ], for example, we start with the augmented matrix [ [ 2  3 | 1  0 ] , [ -4    1 | 0  1 ] ].  Write this matrix out so you can see how the rows compare.  Then add the double of the first row to the second and replace the second row with this row.  What is your result?  Explain how your result got you closer to the desired form [  [1  0 | *  * ], [0  1 | *  * ] ], and indicate the sort of steps you plan to use in order to finish getting the desired form.

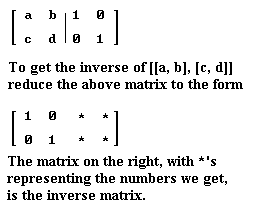
Your solution: 

Confidence Assessment:

Given Solution: 

`aThe first row is [ 2  3  | 1  0 ]; doubling the first row we get [ 4   6 |  2  0 ], which we add to the second row [ -4  1  | 0   1 ] to get [ 0   7 | 2  1 ].  Inserting this into the original matrix in place of the second row we get the matrix

[ [ 2  3 | 1  0 ] , [ 0   7 | 2  1 ] ].

Self-critique (if necessary):

Self-critique Rating:

Question:  `q005.  In the preceding problem you should have obtained the matrix [ [ 2  3 | 1  0 ] , [ 0    7 | 2  1 ] ].  Proceed by first multiplying the second row by 1/7 to get the second row into the desired form.  Then do whatever is necessary to get the first row into the desired form.

Your solution: 

Confidence Assessment:

Given Solution: 

`aMultiplying the second row by 1/7 we get the matrix [ [ 2  3 | 1  0 ] , [ 0   1 | 2/7  1/7 ] ].

We obtain the desired 0 in the second position of the first row by adding -3 * second row to the first row and replacing the first we get [ [ 2  0 | 1/7  -3/7 ] , [ 0   1 | 2/7   1/7 ] ].

We now want the 1 in the first position of the second row.  1/2 * first row accomplishes this and gives us the matrix

[ [ 1  0 | 1/14  -3/14 ] , [ 0   1 | 2/7  1/7 ] ].

This matrix has the desired form, with the identity matrix formed by the first two columns.  The last two columns therefore constitute the inverse of the original matrix.

These steps are illustrated in Figure 92.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q006.  The matrix [ [ 1  0 | 1/14  -3/14 ] , [ 0   1 | 2/7   1/7 ] ] obtained by reducing the matrix [ [ 2  3 | 1  0 ] , [ -4    1 | 0  1 ] ] consists of the identity matrix augmented by the matrix [ [ 1/14   -3/14 ], [ 2/7   1/7] ].  This matrix is the inverse A^-1 = [ [ 1/14   -3/14 ], [ 2/7   1/7] ].  Show that this matrix is indeed the inverse by showing that A * A^-1 = I, the identity matrix, and also that A^-1 * A = I.

Your solution: 

Confidence Assessment:

Given Solution: 

`aFigure 96 shows both products, each obtained by the usual method of matrix multiplication (each row of the first matrix multiplied by each column of the second with the results positioned as usual in the product matrix).  We see that both product give us the identity matrix.

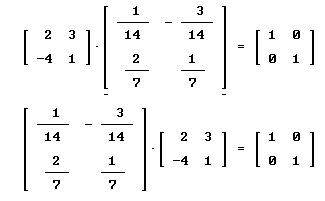
Self-critique (if necessary):

Self-critique Rating:

Question:  `q007.  Write the system 2 x + 3 y = -6, -4 x + y = 8 as a matrix equation A * X = C.  Give the matrices A, X and C.

Self-critique (if necessary):

Self-critique Rating:

Question:  `q008.  The inverse of the matrix A = [ [ 2  3 ], [ -4   1 ] ] is the matrix A^-1 = [ [ -1/14   -3/14 ], [ 2/7   1/7] ], as found in the preceding series of questions. 

If we multiply both sides of the matrix equation A * X = C by this inverse we get A^-1 * A * X = A^-1 * C; since A^-1 * A = I we thus have X = A^-1 * C.

Calculate A^-1 * C.  Then using this result write out the matrices in the equation X = A^-1 * C.  What does this tell you about the values x and y that satisfy the given system of equations?

Your solution: 

Confidence Assessment:

Given Solution: 

`aFigure 98 shows the original matrix equation translated into the symbolic algebraic form

A X = C.  This equation is then multiplied on sides A^-1, resulting in the equation

A^-1 * A * X = A^-1 * C.

Since A^-1 * A = I, the identity matrix, the left-hand side becomes I * X; and since I is the identity matrix we know that I * X = X so we have

X = A^-1 * C.

Translating this back into matrix form we have [ 1/14, - 3/14], [ 2/7, 1/7] ] * [ -6, 8 ],

with the result as shown in the figure.  Our solution is [ -15/7, -4/7 ].

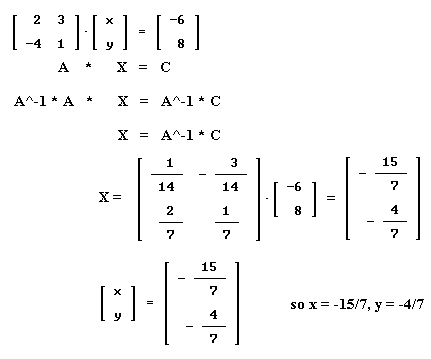
Self-critique (if necessary):

Self-critique Rating:

Question:  `q009.  Apply the techniques of this assignment to find the solution of the system 3 x - 2 y = 10, -5 x + 3 y = -13.

Your solution: 

Confidence Assessment:

Given Solution: 

`aThe system can be expressed as the product

[ [ 3  -2 ], [ -5  3 ] ] * [ x   y ]` = [ 10  -13 ]`

which is of form A X = C with A = [ [ 3  -2 ], [ -5  3 ] ] and C = [ 10  -13 ]`. 

The solution of the equation A X = C will be X = A^-1 * C, easily obtained if we can find A^-1.

The inverse of A is obtained by reducing the augmented matrix

[ A | I ] =  [ [ 3  -2  | 1  0 ], [ -5  3 | 1  0 ] ]

to the form [ I | * ] = [[ 1  0  | *  * ], [ 0  1 | *  * ] ], with the * matrix being A^-1. 

Figure 113 illustrates the reduction of the original matrix to the desired form, with the result that the inverse is

A^-1 = [ [3/19, -2/19], [5/19, 3/19] ].

We now calculate our solution X = A^-1 * C:

X = [ [3/19, -2/19], [5/19, 3/19] ] * [ 10 -13 ]` = [56/19, 11/19]` = [x, y']`.

Thus x = 56/19 and y = 11/19, or in approximation x = 2.95, y = .58.

Self-critique (if necessary):

Self-critique Rating: