If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
016. Sequences and Series
Question: `q001. What is the pattern of the sequence 2 6 10 14 18 ... ? If this pattern holds what is the value of the 100th member of this sequence? In terms of the symbol n, what is the value of the nth number in this sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aThe pattern is fairly easy to see. Each member of the sequence is 4 greater than the preceding member.
To get to the 2d member of the sequence we can start at 2 and make a 'jump' of 4 units each, ending up at 6.
To get to the 3d member of the sequence we can start at 2 and make 2 'jumps' of 4 units each.
The number of 'jumps' necessary to reach the numbers in the second and third positions of the sequence will be 1 and 2, respectively. The number of 'jumps' therefore appears to the 1 less than the position of the number.
It should be clear that this pattern will continue, with each succeeding position of the sequence corresponding to an additional 'jump' of 4 units.
It follows that the 100th member of the sequence can be found by starting at 2 and making 99 'jumps' of 4 each. 99 'jumps' of 4 each will make a net 'jump' of 4 * 99 = 396 units. Starting from 2 this will bring us to 396 * 2 = 398.
The 100th member of the sequence will therefore be
2 + 99 * 4 = 398.
STUDENT COMMENT
ok forgot to add the 2 which was the
starting number
still dont understand what the nth number is
INSTRUCTOR COMMENT
If n = 100, then as seen above the nth
term, in this case the 100th term, is 398. To get to 398 we would start at the
first number 2 and make 99 'jumps', each of 4 units. Our total 'jump' would be
99 * 4 = 396, so we would end up at 396 + 2 = 398.
If n was, say, 300, then the nth term would be 1198. To get this we would start
at the first number 2 and make 299 'jumps', each of 4 units. Our total 'jump'
would be 299 * 4 = 1196, so we would end up at 116 + 2 = 1198.
We don't want to have to figure this every time we want to find a certain number
in the sequence. So we reason as follows:
To get the nth number, whatever n might be, we start at the first number 2 and
make n - 1 'jumps', each of 4 units. Our total 'jump' would then be (n - 1) * 4,
so we would end up at (n - 1) * 4 + 2 = 4 * n - 4 + 2 = 4 * n - 2. That is, the
nth number in the sequence is 4 n - 2.
Self-critique (if necessary):
Self-critique Rating:
Question: `q002. What is the pattern of the sequence 1 2 3 4 ... ? What is the value of the 100th member of this sequence? What is the sum of the first 100 numbers in this sequence? What is the value of the nth member of this sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aThe pattern of this sequence is as obvious as it seems. We are adding 1 with each additional position. The 1st member is 1, the 2d member is 2, the 3d member is 3, etc.. The 100th member is 100.
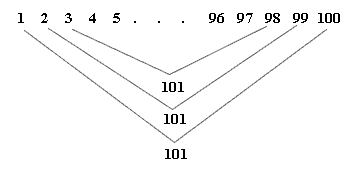
To get the sum of the first 100 members of the sequence we can use the pattern illustrated in Figure 102, grouping 1 with 100 to get 1 + 100 = 101, then 2 with 99 to get 2 + 99 = 101, then 3 with 98 to get 3 + 98 = 101, etc..
It should be clear that following this pattern we will obtain 1 such pair for every 2 numbers, for a total of 100 / 2 = 50 pairs. Each pair will total 101 so the sum of all the numbers is 50 * 101 = 5050.

The nth member of this sequence is just n.
Self-critique (if necessary):
Self-critique Rating:
Question: `q003. If we want to find the sum of the first n members of the sequence 1 2 3 4 ... , we can as in the solution to the preceding question pair the numbers in such a way that each pair adds up to the same thing. How many pairs will we get from the first n members of the sequence? What is the first of the n members and what is the last? What is their sum? What is the second of the n member and the second to the last? What is their sum? What pattern do you see here and how can it help you find the sum of the first n members? What is your expression for the sum of the first n members of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
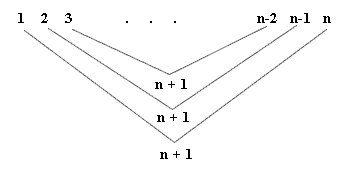
`a To get the sum of the first n members of the sequence we can use the pattern illustrated in Figure 107, grouping 1 with n to get 1 + n = n + 1, then 2 with n - 1 to get 2 + (n-1) = n + 1, then 3 with n - 2 to get 3 + (n - 2) = n + 1, etc..
It should be clear that following this pattern we will obtain 1 such pair for every 2 numbers, for a total of n / 2 pairs. Each pair will total n + 1 so the sum of all the numbers is n/2 * (n + 1) = n ( n + 1) / 2.
ALTERNATIVE EXPLANATION:
The first n members of the sequence are 1, 2, 3, 4, 5, ... (n-2), (n-1), n.
The first and last numbers in the sequence are 1 and n, so they add up to n + 1.
Since the sequence increases by the same number each time, the second number and the second-to last number add up to the same number, and it should be clear that the rest of the sequence can be paired up in a similar manner.
There are n numbers in the sequence, so there are n / 2 pairs.
The sum of the first n numbers is therefore equal to the number of pairs, multiplied by the sum of each pair so that
sum of first n numbers = (n / 2) * ( n + 1).
Self-critique (if necessary):
Self-critique Rating:
Question: `q004. Adapt the reasoning process used in the preceding two questions to find the sum of the first 100 members of the sequence 2 6 10 14 18 ... . Find the expression for the nth member and determine the sum of the first n members of this sequence.
Your solution:
Confidence Assessment:
Given Solution:
`aIn the first problem we saw that the 100th member of the sequence 2 6 10 14 ... is 2 + 99 * 4 = 398.
The sum of the first and last numbers is therefore 2 + 389 = 400, while the sum of the second and next-to-last numbers is 6 + 394 = 400.
It should be clear that we can continue pairing the numbers in this manner, obtaining the sum 400 for each pair.
We have 100 numbers so we have 100 / 2 = 50 pairs.
The total of 50 pairs each adding up to 400 is 50 * 400 = 20,000. The first 100 numbers in this sequence therefore total 20,000.
The first n members of the sequence are 2, 6, 10, 14, ..., 4 n - 2.
The first and last numbers in the sequence are 1 and 4 n - 2, so they add up to 4 n - 1.
Since the sequence increases by the same number each time, the second number and the second-to last number add up to the same number, and it should be clear that the rest of the sequence can be paired up in a similar manner.
The sequence 'jump' in units of 4, so only every fourth integer between 2 and 4 n - 2 occurs in the sequence
There are thus n / 4 numbers in the sequence, so there are 1/2 ( n / 4) = n / 8 pairs.
n / 8 pairs, each adding up to 4 n - 2, yields a total of (n / 8) * (4 n - 2) = (2 n^2 - n) / 4.
Self-critique (if necessary):
Self-critique Rating:
Question: `q005. What is the pattern of the sequence 1 2 4 8 16 32 . . . ? What is the 30th member of this sequence? What is the expression for the nth member of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
`a Each member of this sequence is double the preceding member. The second element is 2 * 1, the third is 4 = 2 * 2 = 2 * 2, the fourth is 8 = 2 * 4 = 2 * 2 * 2, etc..
Another way of saying this is to say that the second element is 2^1, the third is 2^2, the fourth is 2^3, etc.. The power of 2 is always 1 less than the position in the sequence.
The 30th member will therefore be 2^(30-1) = 2^29 = 536,870,912.
To get the nth member you start with 1 and multiply by 2, a total of n - 1 times.
Multiplying by 2 a total of n - 1 times is the same as multiplying by 2^(n - 1).
The nth member is therefore 1 * 2^(n - 1), or just 2^(n - 1).
Self-critique (if necessary):
Self-critique Rating:
Question: `q006. What is the pattern of the sequence 6 12 24 48 96 192 . . . ? What is the 30th member of this sequence? What is the expression for the nth member of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
`a Each member of this sequence is double the preceding member. The second element is 12 = 2 * 6, the third is 24 = 2 * 2 * 6 = 2^2 * 6, the fourth is 48 = 2 * 2 * 2 * 6 = 2^3 * 6, etc..
Again the power of 2 is always 1 less than the position in the sequence, and is multiplied by the first number in the sequence (i.e., by 6 in this example).
The 30th member will therefore be 6 * 2^(30-1) = 6 * 2^29 = 3,221,225,472.
To get the nth member you start with 6 and multiply by 2, a total of n - 1 times.
Multiplying by 2 a total of n - 1 times is the same as multiplying by 2^(n - 1).
The nth member is therefore 6 * 2^(n - 1).
Self-critique (if necessary):
Self-critique Rating:
Question: `q007. What is the pattern of the sequence 4 2 1 1/2 1/4 1/8 . . . ? What is the 30th member of this sequence? What is the expression for the nth member of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aEach member of this sequence is half the preceding member. The second element is 2 = 1/2 * 4, the third is 1 = 1/2 * 1/2 * 4 = 1/2^2 * 4, the fourth is 1/2 = 1/2 * 1/2 * 1/2 * 4 = 1/2^3 * 4, etc..
The power of 1/2 is always 1 less than the position in the sequence, and is multiplied by the first number in the sequence (i.e., by 4 in this example).
The 30th member will therefore be 4 * 1/2^(30-1) = 4 * 1/2^29 = 4 * 1/536870912 = 1/134217728 (this is exact, and is approximately equal to .000000007450580596, or equivalently to 7.450580596 * 10^-9).
To get the nth member you start with 1 and multiply by 1/2, a total of n - 1 times.
Multiplying by 1/2 a total of n - 1 times is the same as multiplying by (1/2)^(n - 1).
The nth member is therefore 1 * (1/2)^(n - 1), or just (1/2)^(n - 1).
Self-critique (if necessary):
Self-critique Rating:
Question: `q008. The second partial sum of the sequence 4 2 1 1/2 1/4 1/8 . . . is 4 + 2 = 6. The third partial sum is 4 + 2 + 1 = 7. What are the fourth, fifth, sixth, seventh and eighth partial sums? Do the partial sums of this sequence have an upper bound--i.e., is there a number the partial sums can never exceed?
Your solution:
Confidence Assessment:
Given Solution:
`aThe fourth partial sum is 4 + 2 + 1 + 1/2 = 7 1/2.
The fifth partial sum is 4 + 2 + 1 + 1/2 + 1/4 = 7 3/4.
The sixth partial sum is 4 + 2 + 1 + 1/2 + 1/4 + 1/8 = 7 7/8.
The seventh partial sum is 4 + 2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 = 7 15/16.
The eighth partial sum is 4 + 2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 = 7 31/32.
Self-critique (if necessary):
Self-critique Rating:
Question: `q009. The partial sums of the sequence 4 2 1 1/2 1/4 1/8 . . . are 4, 6, 7, 7 1/2, 7 3/4, 7 7/8, 7 15/16, ... . What is the pattern to these partial sums? Will the partial sum ever exceed 8? Is there any limit to how close the partial sums can get to 8?
Your solution:
Confidence Assessment:
Given Solution:
`aThe partial sums can be compared with 8:
7 1/2 is 1/2 less than 8
7 3/4 is 1/4 less than 7
7 7/8 is 1/8 less than 8
7 15/16 is 1/16 less than 8
7 31/32 is 1/32 less than 8.
Each partial sum is twice as close to 8 as the last number added.
Since the last number added will always be positive but will eventually be as small as we might wish, if this pattern continues (as it does) we expect that the partial sums will approach as close as we wish to 8 without ever reaching 8.
Self-critique (if necessary):
Self-critique Rating:
Question: `q010. If a sequence can be written in the form a * r^0, a * r^1, a * r^2, a * r^3, ..., a * r^n, ... that sequence is said to be a geometric sequence with common ratio r. How can the sequence 4, 2, 1, 1/2, 1/4, 1/8, . . . be expressed in the given form? Give the values of r and a that put the sequence into this form.
Your solution:
Confidence Assessment:
Given Solution:
`aThe sequence 4, 2, 1, 1/2, 1/4, 1/8, . . . be expressed in the given form by first factoring out the 4 to obtain the form
4 ( 1, 1/2, 1/4, 1/8, . . . ).
The common ratio of the sequence is found by dividing each member of the sequence by its predecessor:
r = 2/4 = 1/2, or r = 1/2, or r = 1/2 / (1/4) = 1/2.
We always get the same result so r = 1/2.
The sequence 1, 1/2, 1/4, 1/8, . . . is expressed in terms of powers of r as
1, 1/2, 1/4, 1/8, . . . = (1/2)^0, (1/2)^1, (1/2)^2, (1/2)^3, . . . = r^0, r^1, r^2, r^3, . . .
Thus we say that sequence
4, 2, 1, 1/2, 1/4, 1/8, . . .
is expressed in standard form a * r^0, a * r^1, a * r^2, a * r^3, ..., a * r^n, . . . as
4 ( (1/2)^0, (1/2)^1, (1/2)^2, (1/2)^3, . . . ).
Self-critique (if necessary):
Self-critique Rating:
Question: `q011. The sequence r^0, r^1, r^2, ... , r^n, ... has the property that its (n+1)th partial sum, which is 1 + r + r^2 + r^3 + ... + r^n, is equal to Sn = ( 1 - r^n ) / ( 1 - r). What therefore is the value of the 11th partial sum of the sequence 1, 1/2, 1/4, 1/8, ..., 1/n, ... ?
Your solution:
Confidence Assessment:
Given Solution:
`a The 11th partial sum is the n = 11-1 = 10 value of the expression Sn = (1 - r^n ) / ( 1 - r ) for the sequence 1, 1/2, 1/4, 1/8, . . ., 1/n, . . . with r = 1/2. We get
S10 = (1 - (1/2)^10) / ( 1 - 1/2) = (1 - 1/1024) / (1 - 1/2) = (1023 / 1024) / (1/2) = 2 * (1023 / 1024) = 2046 / 1024 = 1 511/512.
Self-critique (if necessary):
Self-critique Rating:
Question: `q012. What is the value of the 10th partial sum of the sequence 4, 2, 1, 1/2, 1/4, 1/8, ... ? What is the value of the nth partial sum of this sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aAs seen previously we can write this sequence as
4 (1 + 1/2 + 1/4 + 1/8 + . . . + (1/2)^n + . . .). The 11th partial sum of 1 + 1/2 + 1/4 + 1/8 + . . . + (1/2)^n + . . . is the n = 11-1 = 10 value of the expression Sn = (1 - r^n ) / ( 1 - r ) with r = 1/2. We get
S10 = (1 - (1/2)^10) / ( 1 - 1/2) = (1 - 1/1024) / (1 - 1/2) = (1023 / 1024) / (1/2) = 2 * (1023 / 1024) = 2046 / 1024.
The 10th partial sum of the original sequence is thus
4 (1 + 1/2 + 1/4 + 1/8 + . . . + (1/2)^n + . . .) = 4 * 2046 / 1024 = 2046 / 256 = 7 254/256 = 7 127/128.
Your solution:
Confidence Assessment:
Given Solution:
`a
Self-critique (if necessary):
Self-critique Rating:
Question: `q013. A sequence is defined by the expression a(n) = 4 n - 3. What are the values of a(1), a(2), a(3) and a(4)? What are the first four partial sums of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aTo get a(1) we substitute n = 1 into the expression a(n) = 4 n - 3, obtaining a(1) = 4 * 1 - 3 = 1. Similarly we get
a(2) = 4 * 2 - 3 = 5,
a(3) = 4 * 3 - 3 = 9,
a(4) = 4 * 4 - 3 = 13.
The partial sums are
S1 = 1,
S2 = 1 + 5 = 6,
S3 = 1 + 5 + 9 = 15,
S4 = 1 + 5 + 9 + 13 = 28.
Self-critique (if necessary):
Self-critique Rating:
Question: `q014. A sequence is defined by the expression a(n) = 4 * 3^(n-1). What are the values of a(1), a(2), a(3) and a(4)? What are the first four partial sums of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
`aTo get a(1) we substitute n = 1 into the expression a(n) = 4 * 3^(n-1), obtaining a(1) = 4 * 3^(1-1) = 4 * 3^0 = 4 * 1 = 4. Similarly we get
a(2) = 4 * 3^(2-1) = 4 * 3 = 12,
a(3) = 4 * 3^(3-1) = 4 * 3^2 = 36,
a(4) = 4 * 3^(4-1)= 4 * 3^3 = 4 = 108.
The partial sums are
S1 = 4,
S2 = 4 + 12 = 16,
S3 = 4 + 12 + 36 = 52,
S4 = 4 + 12 + 36 + 108 = 160.
Self-critique (if necessary):
Self-critique Rating:
Question: `q015. A sequence is defined by the expression a(n) = 4 * (-1/2)^(n-1). What are the values of a(1), a(2), a(3) and a(4)? What are the first four partial sums of the sequence?
Your solution:
Confidence Assessment:
Given Solution:
To get a(1) we substitute n = 1 into the expression a(n) =
4 * (-1/2)^(n-1), obtaining a(1) = 4 * (-1/2)^(1-1) = 4 * (-1/2)^0 = 4 * 1 = 4.
Similarly we get
a(2) = 4 * (-1/2)^(2-1) = 4 * (-1/2) = -2,
a(3) = 4 * (-1/2)^(3-1) = 4 * (-1/2)^2 = 1,
a(4) = 4 * (-1/2)^(4-1)= 4 * (-1/2)^3 = -1/2..
The partial sums are
S1 = 4,
S2 = 4 + (-2) = 2,
S3 = 4 + (-2) + 1 = 3,
S4 = 4 + (-2) + 1 + (-1/2) = 2 1/2.
Self-critique (if necessary):
Self-critique Rating: