'Flow diagrams' as a guide to reasoning
Many students have had questions about
the idea of 'flow diagrams', either because the concept is very new or because
the information given in assignments has been skipped or missed.
A number of questions from students have
motivated this expanded discussion, including the following question from a very
capable and conscientious student answering the Query of Assignment 5:
-
I am really struggling with the different levels here.
I can use the given information to solve for the information we
need, but Iím having trouble making connections to the different levels.
I have tried to draw out and write out a chart from doing the work on
my own and when working through the given solution.
-
Is there an additional reference I can look at, read,
or do some practice problems to try to get this?
-
I do know that the equation 'ds
= (v0 +
vf ) /
2 * 'dt
can be used to find `ds, if we know v0, vf and `dt. Knowing `ds, I
know that I can then figure out the other information. I just don't
understand the flow diagram idea.
Note also that this question is very
well-posed, telling me exactly what he knows and doesn't know
If well-prepared and conscientious
students have either missed seeing the idea, or has trouble understanding it,
then it's obvious that the entire idea needs to be addressed.
This document is therefore designed to
further explain the idea to those who have difficulty with the concept,
and to 'fill in the blanks' for those who have missed seeing the
information.
We will develop the 'flow diagram' for
reasoning out a uniform-acceleration situation in which we are given v0, vf
and `dt for uniformly accelerated motion on a specific interval.
Note that assigned Class Notes and
Introductory Problem Sets include further explanations and examples of the 'flow
diagram' idea and its applications.
The first two levels of the
diagram
The 'flow diagram' begins by listing the
symbols for the given quantities v0, vf and `dt. We call these our
first-level quantities. Our diagram will trace out how
we use these quantities to progressively reason out the remaining
quantities.
Of the seven quantities in terms
of which we reason out uniformly accelerated motion we have be given
three, v0, vf and `dt. Thus four remain, namely a, `ds, `dv and
v_Ave.
From the initial and final velocities
v0 and vf we know that we can find the change in velocity and the
average velocity:
-
The change in a quantity
during an interval is equal to the difference between its initial
value and its final value, which is obtained by subtracting
the initial value from the final. It is therefore
clear that if we know the initial and final velocities, we can directly
obtain the change in velocity.
-
We know that if acceleration
is uniform, average velocity is equal to the average of
initial and final velocities. We are assuming uniform
acceleration, so knowing the initial and final velocities we can clearly
determine the average velocity.
We indicate this on our diagram by
writing down the symbols `dv and v_Ave for change in velocity and average
velocity, and drawing lines to indicate the 'first-level' quantities from which
they are determined.
Especially when first using 'flow
diagrams' we will generally list our 'first-level' quantities in a single
line at the top of our diagram. Then we will list our second-level
quantities on a single line, lower on the diagram. Following this
pattern, our third-level quantities are listed on a line lower than the
second, etc..
Our lines at this point are listed
as

with the first line indicating our
initial quantities and the second line the quantities we can reason out from
them.
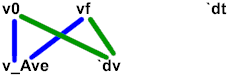
v_Ave is also found from v0 and vf.
We will therefore draw lines from v0 and vf to the symbol v_Ave.
Including the lines (using blue
lines to indicate that v_Ave comes from v0 and vf, and green lines to
indicate that `dv comes from v0 and vf), our picture now looks like the
following:
Moving on
to the third level; reasoning 'forward' and 'backward'
At this point of our reasoning we know
v0, vf and `dt (our 'first-level' quantities), and we know how to find `dv and
v_Ave (which are 'second-level' quantities).
Of the seven quantities in terms of
which we understand uniformly accelerated motion, we therefore know all but two.
The two we don't know are `ds and a_Ave.
We can 'think forward', starting
with what we know, and asking ourselves how our known quantities might be
combined to obtain new information.
Or we can 'think backward', starting
with the definitions of our remaining unknown quantities, and see if those
definitions fit in with our known quantities.
To illustrate both ways of thinking, we
will reason out how to find our average acceleration a_Ave by 'thinking
forward', then reason out it out once again by 'thinking backward'.
-
We start by asking ourselves what we
can find from what we know. We know v0, vf, `dt, `dv and v_Ave. What
can be combined with what in this list to find new information?
-
If we think through the quantities
we have, considering how to combine them, it might strike us that `dv and `dt,
being respectively the change in velocity and the change in clock time, can
be combined to find the average rate of change of velocity with respect to
clock time.
-
Then again, this might not strike us
immediately. So it's worth looking at the chain of thinking that might
lead us to this conclusion:
Going back to our list v0, vf, `dt,
`dv and a_Ave, we methodically begin to think through the possible
combinations.
Our first-level quantities v0 and vf
have already been combined to find `dv and vAve. So we have already
done everything we can think of with these two quantities.
Our remaining first-level quantity
is `dt. Can `dt be combined with anything on our 'known list' to find
useful new information?
`dt combined with v0 to figure
out how far we would go (or more precisely our displacement) if we
maintained the initial velocity v0 for the entire interval; however
since velocity changes that situation doesn't really occur. Or we
could combine `dt with vf, but again vf represents the velocity only at
the end of the interval; this velocity isn't maintained for the entire
interval.
Moving on to our second-level
quantities, `dt (change in clock time) combined with `dv (change in
velocity) can clearly be used to find an average rate of change.
We could apply the definition of average rate of change to find either
the average rate of change of clock time with respect to velocity, or
the average rate of change of velocity with respect to clock time.
We should recognize the latter as the average acceleration.
Thus `dv and `dt can be combined
to find the average rate of change of velocity with respect to clock
time, which is the average acceleration a_Ave.
Thus by combining `dv and `dt we
have found a new quantity, a_Ave. This is a third-level quantity,
since to find it we had to use the second-level quantity `dv.
This is an example of 'thinking
forward'. Whether immediately or through methodically thinking through
possible combinations, we found that `dv and `dt can be used to find a_Ave.
We will place a_Ave at the 'third
level' and connect it with lines to `dv and `dt, the quantities from which
is is calculated.
a_Ave is the average acceleration,
defined to be the average rate of change of velocity with respect to clock
time. By the definition of average rate, this is (change in velocity)
/ (change in clock time), or `dv / `dt.
Thus we can find a_Ave if we know `dv
and `dt.
Looking at our known quantities, we
find that `dv and `dt are among them.
Just as before we conclude that
a_Ave can be reasoned out from our known quantities `dv and `dt, so we place
a_Ave at the 'third level' and connect it with lines to `dv and `dt, the
quantities from which is is calculated.
It might seem from above that 'thinking
backward' is easier. It's certainly shorter. However note that you
didn't see the 'thinking-backward' solution until after you had seen the
'forward' reasoning. So you might not be in a position to judge which is
the easier.
In general it turns out there is no
clear consistent choice for which 'reasoning direction', forward or backward, is
easier. It depends on the situation, and it often depends even more on how
your mind works, on how your brain happens to be 'wired' and how your previous
experiences have influenced your ways of thinking.
We still have `ds to reason out.
We can do so by 'thinking forward' or 'thinking backward'.
-
It's probably more difficult to
reason out `ds by 'thinking backward'. This is because, unlike a_Ave
in the preceding, `ds is not defined in terms of the other quantities.
So you don't have an obvious definition to use.
However this doesn't mean you don't
have any definitions available. `ds is certainly involved in at least
one other definition.
`ds represents change in position.
One of our most basic definitions involves change in position: our
definition of average rate of change of position with respect to clock time,
i.e., average velocity. Thus v_Ave = `ds / `dt.
Knowing that v_Ave = `ds / `dt, we
can look back at our known quantities v0, vf, `dt, v_Ave, a_Ave and `dv and
quickly see that we know v_Ave and `dt. Thus we will be able to solve
v_Ave = `ds / `dt for `ds, obtaining
`ds = v_Ave / `dt.
Looking at our known quantities v0,
vf, `dt, v_Ave, `dv and a_Ave, if we systematically 'pair up' quantities we
will soon be lead to consider what we can find from `dt and v_Ave.
When we think about v_Ave, we should
recall that its definition leads us to understand that v_Ave = `ds / `dt.
Now, knowing v_Ave and `dt, we can solve for `ds, again obtaining
`ds = v_Ave / `dt.
The difference, in this example, between
'thinking forward' and 'thinking backwards' might be summarized in the following
statements:
-
When we 'think forward', v_Ave is on
our list of known quantities, so we are logically led to consider v_Ave.
-
When we 'think backward' we have to
think of the definition, but without a list of known quantities to guide us.
The diagram at the third level
With `ds and a_Ave on the 'third level',
our diagram is now as follows:

Adding lines to indicate the new
relationships, using 'red' lines to indicate the reasoning of `ds and 'purple'
lines for a_Ave, we have our final diagram:
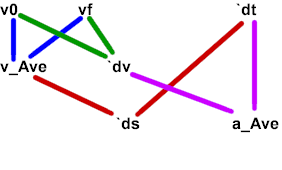
Summary
Summarizing, we see that the above
diagram is on three levels:
-
The first level indicates our given
information v0, vf and `dt.
-
The second level indicates the
quantities v_Ave and `dv, obtained using first level quantities.
-
The third level indicates the
quantities `ds and a_Ave, both of which require second-level quantities (as
well as a first-level quantity).
-
The 'blue' lines indicate the
quantities used to find v_Ave.
-
The 'green' lines indicate the
quantities used to find v_Ave.
-
The 'red' lines indicate the
quantities used to find v_Ave.
-
The 'purple' lines indicate the
quantities used to find v_Ave.
Further
thoughts
Once we understand the relationships ...
:
Once we really understand the
relationships among the seven quantities v0, vf, `dt, v_Ave, `dv, a_Ave and
`ds, we will spontaneously be able to think about a given situation in
whichever 'direction' has become more natural to us.
-
For example, we will get used to
the idea that once we know two of the three quantities v_Ave, `ds and `dt,
we can find the other, and it won't matter much to us whether we think
of this from the 'forward' or 'backward' perspective.
-
When we are still 'sorting out'
these ideas, though, it's a good idea to consciously approach a question
from both directions.
Sometimes we really do need the
equations:
In some cases, reasoning in the way
illustrated here turns out to be impossible and we must rely on equations
(this is the case if we are given a, `dt and either v0 or vf; the
definitions alone aren't sufficient, at least without using more mathematics
than we wish). However in all other cases, if we know three of the
five quantities v0, vf, `dt, a and `ds, we can reason out the values of the
seven quantities v0, vf, `dt, a, `ds, `dv and v_Ave.



