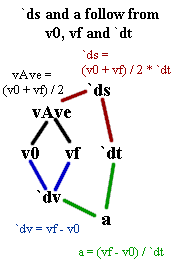
If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.
005. Uniformly Accelerated Motion
Preliminary notes:
On any interval there are seven essential quantities in terms of which we analyze the motion of a nonrotating object:
You should remember these symbols and their meanings. You will be using them repeatedly, and you will soon get used to them.
You will of course improve your understanding and appreciation of these quantities as you work through the qa and the associated questions and problems.
Note also that `dt = t_f - t_0, where t_f represents the final clock time and t_0 the initial clock time on the interval, and that `ds = s_f - s_0, where s_f represents the final position and t_0 the initial position of the object on the interval.
Further discussion of symbols (you can just scan this for the moment, then refer to it when and if you later run into confusion with notation)
the symbol x is often used instead of s for the position of an object moving along a straight line, so that `dx might be used instead of `ds, where `dx = x_f - x_0
some authors use either s or x, rather that s_f or x_f, for the quantity that would represent final position on the interval; in particular the quantity we express as `dx might be represented by x - x_0, rather than x_f - x_0
some authors use t instead of `dt; there are good reasons for doing so but at this point in the course it is important to distinguish between clock time t and time interval `dt; this distinction tends to be lost if we allow t to represent a time interval
the quantity we refer to as `dt is often referred to as 'elapsed time', to distinguish it from 'clock time'; once more we choose here to use different symbols to avoid confusion at this critical point in the course)
If the acceleration of an object is uniform, then the following statements apply. These are important statements. You will need to answer a number of questions and solve a number of problems in order to 'internalize' their meanings and their important. Until you do, you should always have them handy for reference. It is recommended that you write a brief version of each statement in your notebook for easy reference:
1. A graph of velocity vs. clock time forms a straight line, either level or increasing at a constant rate or decreasing at a constant rate.
2. The average velocity of the object over any time interval is equal to the average of its velocity at the beginning of the time interval (called its initial velocity) and its velocity at the end of the time interval (called its final velocity).
3. The velocity of the object changes at a constant rate (this third statement being obvious since the rate at which the velocity changes is the acceleration, which is assumed here to be constant).
4. The acceleration of the object at every instant is equal to the average acceleration of the object.
Question: `q001. Note that there are 13 questions in this assignment.
Suppose that an object increases its velocity at a uniform rate, from an initial velocity of 5 m/s to a final velocity of 25 m/s during a time interval of 4 seconds.
By how much does the velocity of the object change?
What is the average acceleration of the object?
What is the average velocity of the object?
(keep your notes on this problem, which is continued through next few questions)
Your solution:
Confidence rating:
Given Solution:
The velocity of the object changes from 5 meters/second to 25 meters/second so the change in velocity is 20 meters/second. The average acceleration is therefore (20 meters/second) / (4 seconds) = 5 m / s^2. The average velocity of the object is the average of its initial and final velocities, as asserted above, and is therefore equal to (5 meters/second + 25 meters/second) / 2 = 15 meters/second (note that two numbers are averaged by adding them and dividing by 2).
Self-critique (if necessary):
Self-critique rating:
Question: `q002. How far does the object of the preceding problem travel in the 4 seconds?
Your solution:
Confidence rating:
Given Solution:
The displacement `ds of the object is the product vAve `dt of its average velocity and the time interval, so this object travels 15 m/s * 4 s = 60 meters during the 4-second time interval.
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Explain in commonsense terms how we determine the acceleration and distance traveled if we know the initial velocity v0, and final velocity vf and the time interval `dt.
Your solution:
Confidence rating:
Given Solution:
In commonsense terms, we find the change in velocity since we know the initial and final velocities, and we know the time interval, so we can easily calculate the acceleration. Again since we know initial and final velocities we can easily calculate the average velocity, and since we know the time interval we can now determine the distance traveled.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. Symbolize the situation by first giving the expression for the acceleration in terms of v0, vf and `dt, then by giving the expression for vAve in terms of v0 and vf, and finally by giving the expression for the displacement in terms of v0, vf and `dt.
Your solution:
Confidence rating:
Given Solution:
The acceleration is equal to the change in velocity divided by the time interval; since the change in velocity is vf - v0 we see that the acceleration is a = ( vf - v0 ) / `dt.
The average velocity is the average of the initial and final velocities, which is expressed as (vf + v0) / 2.
When this average velocity is multiplied by `dt we get the displacement, which is `ds = (v0 + vf) / 2 * `dt.
STUDENT SOLUTION (mostly but not completely correct)
vAve = (vf + v0) / 2
aAve = (vf-v0) / dt
displacement = (vf + v0)/dt
INSTRUCTOR RESPONSE
Displacement = (vf + v0)/dt is clearly
not correct, since greater `dt implies greater displacement. Dividing by `dt
would give you a smaller result for larger `dt.
From the definition vAve = `ds / `dt, so the displacement must be `ds = vAve * `dt.
Using your correct expression for vAve you get the correct expression for `ds.
Self-critique (if necessary):
Self-critique rating:
Question: `q006. This situation is identical to the previous, and the conditions implied by uniformly accelerated motion are repeated here for your review: If the acceleration of an object is uniform, then the following statements apply:
1. A graph of velocity vs. clock time forms a straight line, either level or increasing at a constant rate or decreasing at a constant rate.
2. The average velocity of the object over any time interval is equal to the average of its velocity at the beginning of the time interval (called its initial velocity) and its velocity at the end of the time interval (called its final velocity).
3. The velocity of the object changes at a constant rate (this third statement being obvious since the rate at which the velocity changes is the acceleration, which is assumed here to be constant).
4. The acceleration of the object at every instant is equal to the average acceleration of the object.
Describe a graph of velocity vs. clock time, assuming that the initial velocity occurs at clock time t = 0.
At what clock time is the final velocity then attained?
What are the coordinates of the point on the graph corresponding to the initial velocity (hint: the t coordinate is 0, as specified here; what is the v coordinate at this clock time? i.e., what is the velocity when t = 0?).
What are the coordinates of the point corresponding to the final velocity?
Your solution:
Confidence rating:
Given Solution:
The initial velocity of 5 m/s occurs at t = 0 s so the corresponding graph point is (0 s, 5 m/s). The final velocity of 25 meters/second occurs after a time interval of `dt = 4 seconds; since the time interval began at t = 0 sec it ends at at t = 4 seconds and the corresponding graph point is ( 4 s, 25 m/s).
Self-critique (if necessary):
Self-critique rating:
Question: `q007. This situation continues the preceding.
Is the v vs. t graph increasing, decreasing or level between the two points, and if increasing or decreasing is the increase or decrease at a constant, increasing or decreasing rate?
Your solution:
Confidence rating:
Given Solution:
Since the acceleration is uniform, the graph is a straight line. The graph therefore increases at a constant rate from the point (0, 5 m/s) to the point (4 s, 25 m/s).
Self-critique (if necessary):
Self-critique rating:
Question: `q008. What is the slope of the graph between the two given points, and what is the meaning of this slope?
Your solution:
Confidence rating:
Given Solution:
The rise of the graph is from 5 m/s to 25 m/s and is therefore 20 meters/second, which represents the change in the velocity of the object. The run of the graph is from 0 seconds to 4 seconds, and is therefore 4 seconds, which represents the time interval during which the velocity changes. The slope of the graph is rise / run = ( 20 m/s ) / (4 s) = 5 m/s^2, which represents the change `dv in the velocity divided by the change `dt in the clock time and therefore represents the acceleration of the object.
Self-critique (if necessary):
Self-critique rating:
Question: `q009. The graph forms a trapezoid, starting from the point (0,0), rising to the point (0,5 m/s), then sloping upward to (4 s, 25 m/s), then descending to the point (4 s, 0) and returning to the origin (0,0). This trapezoid has two altitudes, 5 m/s on the left and 25 m/s on the right, and a base which represents a width of 4 seconds. What is the average altitude of the trapezoid and what does it represent, and what is the area of the trapezoid and what does it represent?
Your solution:
Confidence rating:
Given Solution:
The two altitudes are 5 meters/second and 25 meters/second, and their average is 15 meters/second. This represents the average velocity of the object on the time interval. The area of the trapezoid is equal to the product of the average altitude and the base, which is 15 m/s * 4 s = 60 meters. This represents the product of the average velocity and the time interval, which is the displacement during the time interval.
STUDENT COMMENT
I understand how to find the average altitude and
multiply it by the amount of seconds. I also understand how to find the area of
the trapezoid. But, again I don’t understand what it repreents, which is the
product of the average velocity and the time interval, or the displacement.
INSTRUCTOR RESPONSE
If you multiply the average velocity on a time interval by the duration of the
interval, you get the displacement.
Since the average altitude represents the average velocity and the width
represents the duration of the time interval, the product therefore represents
the displacement.
Since the product of average altitude and width is area, it follows that this
product represents the displacement.
Self-critique (if necessary):
Self-critique rating:
Question: `q010. Students at this point often need more practice identifying which of the quantities v0, vf, vAve, `dv, a, `ds and `dt are known in a situation or problem. You should consider running through the optional supplemental exercise ph1_qa_identifying_quantities.htm . The detailed URL is http://vhcc2.vhcc.edu/dsmith/genInfo/qa_query_etc/ph1/ph1_qa_identifying_quantities.htm If you are able to quickly identify all the quantities correctly 'in your head', the exercise won't take long and it won't be necessary to type in any responses or submit anything. If you aren't sure of some of the answers, you can submit the document, answer and/or asking questions on only the problems of which you are unsure.
You should take a quick look at this document. Answer below by describing what you see and indicating whether or not you think you already understand how to identify the quantities. If you are not very sure you are able to do this reliably, indicate how you have noted this link for future reference. If you intend to submit all or part of the document, indicate this as well.
Your solution:
Confidence rating:
Given Solution:
You should have responded in such a way that the instructor understands that you are aware of this document, have taken appropriate steps to note its potential usefulness, and know where to find it if you need it.
Self-critique (if necessary):
Self-critique rating:
If you understand the assignment and were able to solve the previously given problems from your worksheets, you should be able to complete most of the following problems quickly and easily. If you experience difficulty with some of these problems, you will be given notes and we will work to resolve difficulties.
Question: `q011. The velocity of a car changes uniformly from 5 m/s to 25 m/s during an interval that lasts 6 seconds. Show in detail how to reason out how far it travels.
Your solution:
Confidence rating:
Question: `q012. The points (5 s, 10 m/s) and (10 s, 20 m/s) define a 'graph trapezoid' on a graph of velocity vs. clock time.
What is the average 'graph altitude' for this trapezoid?
Explain what the average 'graph altitude' means and why it has this meaning.
What is the area of this trapezoid? Explain thoroughly how you reason out this result, and be sure to include and explain your units.
Your solution:
Confidence rating:
Question: `q013. On a certain interval of duration `dt an object has initial velocity v_0 and final velocity v_f. In terms of the symbols v_0, v_f and `dt, what are the values of the following?
Be sure to explain your reasoning.
Your solution:
Confidence rating:
Self-critique (if necessary):
Self-critique rating:
Question: `q014. (University Physics) Given the velocity function
v(t) = 0.1 m/s*3 * t^2 + 2 m/s^2 * t + 4 m/s
evaluate v for t = 5 seconds and for t = 10 second, being sure to verify that the units of our calculation are consistent and that they work out to units of velocity.
On a graph of v vs. t, what would be the coordinates of the points corresponding to t = 5 sec and t = 10 sec?
What would be the area of the 'graph trapezoid' defined by these coordinates, and what does that area mean?
Would this area be the same as, more than, or less than the area under the actual graph of v vs. t.?
What would be the actual area, and what is its meaning?
Your solution:
Confidence rating:
Self-critique (if necessary):
Self-critique rating:
You should submit the above questions, along with your answers and self-critiques. You may then begin work on the Questions, Problem and Exercises, as instructed below.
You should answer the questions and work the problems as given below, as appropriate to your course. Your work should normally be handwritten, should include diagrams and sketches where appropriate, and should go into your Physics notebook (not into your lab notebook).
If the course is not specified for a problem, then students in all physics courses should do that problem.
Principles of Physics students need not do the questions or problems that are specified for General College Physics or University Physics.
General College Physics students need not do questions or problems specified for University Physics.
University Physics students should do all questions and problems.
Principles of Physics students may if they wish do some of the questions and problems specified for General College Physics, but this is neither expected nor required. These problems are accessible to Principles of Physics students, but are generally more challenging that what is expected of students in this course. (Some University Physics problems will also be accessible to Principles of Physics students, though some will not.)
General College Physics students who wish to do so are welcome to work some or all of the University Physics questions and problems, though this is neither expected nor required. Many of the University Physics questions and problems are more challenging than those expected of General College Physics students, and a number of the problems require the use of calculus, which is not expected of General College Physics students.
You are not expected to submit these questions and problems. It would take too much of your time to key in all the answers and solutions. The Query at the end of the assignment will ask you selected questions, which you will at that time be expected to answer based on the work you have done in your notebook.
Questions related to q_a_
1. If we know the initial velocity v0, the final velocity vf and the time interval `dt for the motion of an object, then
2. Suppose we have two points on a straight-line graph of velocity vs. clock time.
3. If we know v0, `dt and a for motion on an interval:
Questions related to Introductory Problem Sets
1. In the figure below the given quantities v0, vf and `dt are listed in a straight line across the middle of the diagram.
There are lines from v0 and vf to vAve, and also from v0 and vf to `dv. Explain how v0 and vf are related to vAve, and also how they are related to `dv.
There are 'red' lines from vAve and `dt to `ds. How are vAve and `dt related to `ds by the definition of average velocity?
There are 'green' lines from `dv and `dt to a. How are `dv and `dt related to a by the definition of average acceleration?
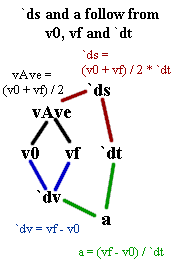
Questions related to Class Notes
1. If a cart is found to have acceleration 30 cm/s^2 when it rolls freely down an incline having slope .05, and acceleration 70 cm/s^2 on an incline having slope .08, then at what average rate is its acceleration changing with respect to ramp slope?
Questions/problems for Principles of Physics Students
4. About how long would it take an automobile moving at the speed limit to travel from Washington, D.C. to Cleveland, Ohio? You may base your answer on any reasonable estimate of the distance and the speed limit, but you should specify your estimates and show how you get from your estimates to your answer.
5. Estimate how long it would take a runner to run from New York to California. You may base your answer on any reasonable estimate of the distance and the running speed, but you should specify your estimates and show how you get from your estimates to your answer.
Questions/problems for General College Physics Students
6. Estimate how many liters of water a human being drinks in a lifetime. Would this water fill an average swimming pool?
Questions/problems for University Physics Students
What is the angle between the between the vectors -2i+6j and 2i - 3j ?
What is the cross product A X B of vector A, whose magnitude is 12.0 meters and which is directed along the negative y axis, and the vector B, with magnitude 18.0 m and directed at 37 deg as measured counterclockwise from the positive x axis? Give both the magnitude and the direction of the cross product.