If your solution to stated problem does not match the given solution, you should self-critique per instructions at
http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm
.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
At the end of this document, after the qa problems (which provide you with questions and solutions), there is a series of Questions, Problems and Exercises.007. Acceleration of Gravity
Question: `q001. We will in this and the next couple of questions obtain an estimate of the acceleration of gravity by determining the slope of an acceleration vs. ramp slope graph for an object gliding down an incline.
Sample data for an object gliding down a 50-cm incline indicate that the object glides down the incline in 5 seconds when the raised end of the incline is .5 cm higher than the lower end; the time required from rest is 3 seconds when the raised end is 1 cm higher than the lower end; and the time from rest is 2 seconds when the raised end is 1.5 cm higher than the lower end.
What is the acceleration for each trial, assuming the acceleration in each to be uniform?
Your solution:
Confidence rating:
Given Solution:
We can find the accelerations either using equations or direct reasoning.
To directly reason the acceleration for the five-second case, we note that the average velocity in this case must be 50 cm/(5 seconds) = 10 cm/s.
Since the initial velocity was 0, assuming uniform acceleration we see that the final velocity must be 20 cm/second, since 0 cm/s and 20 cm/s average out to 10 cm/s.
This implies a velocity change of 20 cm/second a time interval of 5 seconds, or a uniform acceleration of 20 cm/s / (5 s) = 4 cm/s^2.
The acceleration in the 3-second case could also be directly reasoned, but instead we will note that in this case we have the initial velocity v0 = 0, the time interval `dt = 3 sec, and the displacement `ds = 50 cm. We can therefore find the acceleration from the equation `ds = v0 `dt + .5 a `dt^2.
Noting first that since v0 = 0 the term v0 `dt must also be 0,we see that in this case the equation reduces to `ds = .5 a `dt^2. We easily solve for the acceleration, obtaining a = 2 `ds / `dt^2.
In this case we have a = 2 * (50 cm) / (3 sec)^2 = 11 cm/s^2 (rounded to nearest cm/s^2). For the 2-second case we can use the same formula, obtaining a = 2 * (50 cm) / (2 sec)^2 = 25 cm/s^2.
Self-critique (if necessary):
Self-critique rating:
Question: `q002. What are the ramp slopes associated with these accelerations?
Your solution:
Confidence rating:
Given Solution:
For the 5-second trial, where acceleration was 4 cm/s^2, the 'rise' of the ramp was .5 cm and the 'run' was nearly equal to the 50-cm length of the ramp so the slope was very close to .5 cm / (50 cm) = .01.
For the 3-second trial, where acceleration was 11 cm/s^2, the 'rise' of the ramp was 1 cm and the 'run' was very close to the 50-cm length, so the slope was very close to 1 cm / (50 cm) = .02.
For the 2-second trial, where the acceleration was 25 cm/s^2, the slope is similarly found to be very close to 1.5 cm / (50 cm) = .03.
Self-critique (if necessary):
Self-critique rating:
Question: `q003. Sketch a reasonably accurate graph of acceleration vs. ramp slope and give a good description and interpretation of the graph. Be sure to include in your description how the graph points seem to lie with respect to the best-fit straight line (i.e., the straight line that comes as close as possible, on the average, to the three points).
Your solution:
Confidence rating:
Given Solution:
The graph will have acceleration in cm/s^2 on the vertical axis (the traditional y-axis) and ramp slope on the horizontal axis (the traditional x-axis).
The graph points will be (.01, 4 cm/s^2), (.02, 11.1 cm/s^2), (.03, 25 cm/s^2).
The second point lies somewhat lower than a line connecting the first and third points, so the best possible line will probably be lower than the first and third points but higher than the second.
The graph indicates that acceleration increases with increasing slope, which should be no surprise.
It is not clear from the graph whether a straight line is in fact the most appropriate model for the data.
If timing wasn't particularly accurate, these lines could easily be interpreted as being scattered from the actual linear behavior due to experimental errors.
Alternatively the graph could that acceleration vs. ramp slope is increasing at an increasing rate.
STUDENT COMMENT
I am a little unclear about why the lines could be considered scattered from an actual linear behavior, unless it is because the line is not exactly straight and seems to have a curve.
INSTRUCTOR RESPONSE
The graph points don't line along a perfectly straight
line. Based on these three points, you could possibly infer that the graph
curves. A curved graph would be consistent with the
data.
If experimental uncertainties are large enough, the graph could also be
consistent with a best-fit straight line.
The best-fit straight line for this data wouldn't go through any of the graph points; some points will lie above the line and some below.
So the points would to an extent be scattered about the line.
As long as the degree of scattering can be explained by the uncertainties in our measurements, then it is possible that the straight-line, or linear, model is consistent with the data.
Self-critique (if necessary):
Self-critique rating:
Question: `q004. Carefully done experiments show that for small slopes (up to a slope of about .1) the graph appears to be linear or very nearly so. This agrees with theoretical predictions of what should happen. Sketch a vertical line at x = .05. Then extend the straight line you sketched previously until it intersects the y axis and until it reaches past the vertical line at x = .05.
What are the coordinates of the points where this line intersects the y-axis, and where it intersects the x =.05 line? What are the rise and the run between these points, and what therefore is the slope of your straight line?
Your solution:
Confidence rating:
Given Solution:
A pretty good straight line goes through the points (0, -6 cm/s^2) and (.05, 42 cm/s^2). Your y coordinates might differ by a few cm/s^2 either way.
For the coordinates given here, the rise is from -6 cm/s^2 to 42 cm/s^2, a rise of 48 cm/s^2. The run is from 0 to .05, a run of .05. The slope of the straight line is approximately 48 cm/s^2 / .05 = 960 cm/s^2.
Note that this is pretty close to the accepted value, 980 cm/second^2, of gravity. Carefully done, this experiment will give us a very good estimate of the acceleration of gravity.
STUDENT QUESTION
Once I graphed the points using the correct coordinates I was able to see the correct graph, and its slope of 48cm/s^2/ .05 =960cm/s^2.
??????????My question here is what if on my graph the points were at around
42cm/s^2 instead of the 48cm/s^2, and my answer
was 840 or so. Is there room for the variation in how you plot the graph, if I
started with different number or something,
or my graph is not as precise.?????????????????????????
?????????????Also I am still a little
unclear, seeing how I had my point graphed wrong in the first place, about why
we would
use the slope of the graph .5/ 50cm to get .01....I really cannot seem to
rationalize this. ?????????????????????????
INSTRUCTOR RESPONSE
Your slope is based on two points; it can't be calculated based on a single point because you need two points to get the rise and run.
If the two points on your straight line were, say, (0, -10 cm/s^2) and (.05, 48 cm/s^2) then the rise would be 48 cm/s^2 - 10 cm/s^2 = 58 cm/s^2, your run would be .05 and your slope would be 58 cm/s^2 / .05 = 1060 cm/s^2.
If the rise between the two points on your straight line was 42 cm/s^2, with the run still .05, then your slope would be 42 cm/s^2 / .05 = 840 cm/s^2, as you say.
There is in fact only one best-fit line for the data, but since we're estimating the best-fit line it is expected that our estimates of its slope and location will differ somewhat. Certainly it would be possible for one person to get an estimate of 840 cm/s^2, while another might estimate 960 cm/s^2 and another 1060 cm/s^2.
If all three people used the same three data points, and actually found the unique line that best fits those three points, then all three would get identical results.
Self-critique (if necessary):
Self-critique rating:
Question: `q005. The most accurate way to measure the acceleration of gravity is to use the relationship T = 2 `pi / `sqrt(g) * `sqrt(L) for the period of a pendulum.
Use your washer pendulum and time 100 complete back-and-forth cycles of a pendulum of length 30 cm. Be sure to count carefully and don't let the pendulum swing out to a position more than 10 degrees from vertical.
How long did it take, and how long did each cycle therefore last?
Your solution:
Confidence rating:
Given Solution:
100 cycles of a pendulum of this length should require approximately 108 seconds. This would be 108 seconds per 100 cycles, or 108 sec / (100 cycles) = 1.08 sec / cycle. If you didn't count very carefully or didn't time very accurately, you might differ significantly from this result; differences of up to a couple of cycles are to be expected.
Self-critique (if necessary):
Self-critique rating:
Question: `q006. You now have values for the period T and the length L, so you can use the relationship T = 2 `pi / `sqrt(g) * `sqrt(L) to find the acceleration g of gravity. Solve the equation for g and then use your values for T and L to determine the acceleration of gravity.
Your solution:
Confidence rating:
Given Solution:
Solving T = 2 `pi / `sqrt(g) * `sqrt(L) for g, we can first multiply both sides by `sqrt(g) to obtain
T * `sqrt(g) = 2 `pi `sqrt(L).
Then dividing both sides by T we obtain
`sqrt(g) = 2 `pi `sqrt(L) / T.
Squaring both sides we finally obtain
g = 4 `pi^2 L / T^2.
Plugging in the values given here, L = 30 cm and T = 1.08 sec, we obtain
g = 4 `pi^2 * 30 cm / (1.08 sec)^2 = 1030 cm/s^2.
You should check these calculations for accuracy, since they were mentally approximated.
STUDENT QUESTION
I do not understand how if you divide
both sides by the sqrt (g), the you end up with t* sqrt(g) = 2' pi ' sqrt (L),
when sqrt(L) was divided by 2 'pi.......why wouldnt it be t * sqrt (g) = 2'pi /
sqrt(L)....what happens to the division sign there?????
INSTRUCTOR RESPONSE
The division sign is between pi and
sqrt(g). It doesn't apply to sqrt(L).
Multiplications and divisions are done in order, as stated in the order of
operations. This means that you multiply 2 by pi, then divide the result by
sqrt(g), then multiply the result by sqrt(L).
If the sqrt(L) was to be part of the denominator, the expression would have to
be written 2 pi / ( sqrt(g) * sqrt(L) ). In that case you would begin by
multiplying sqrt(g) by sqrt(L), then you would do multiplications and divisions
in order, multiplying 2 by pi then dividing by the product (sqrt(g) sqrt(L)).
The correct expression:
The expression 2 pi / sqrt(g) * sqrt(L) is represented in a computer algebra system as
![]()
This representation is consistent with the order of operations.
The common misinterpretation of the expression:
The expression 2 pi / sqrt(g) * sqrt(L) is often misinterpreted as
![]()
However the above represents 2 pi / (sqrt(g) * sqrt(L) ), not our original expression 2 pi / sqrt(g) * sqrt(L)
Self-critique (if necessary):
Self-critique rating:
Self-critique (if necessary):
Self-critique rating:
You should submit the above questions, along with your answers and self-critiques. You may then begin work on the Questions, Problem and Exercises, as instructed below.
You should answer the questions and work the problems as given below, as appropriate to your course. Your work should normally be handwritten, should include diagrams and sketches where appropriate, and should go into your Physics notebook (not into your lab notebook).
If the course is not specified for a problem, then students in all physics courses should do that problem.
Principles of Physics students need not do the questions or problems that are specified for General College Physics or University Physics.
General College Physics students need not do questions or problems specified for University Physics.
University Physics students should do all questions and problems.
Principles of Physics students may if they wish do some of the questions and problems specified for General College Physics, but this is neither expected nor required. These problems are accessible to Principles of Physics students, but are generally more challenging that what is expected of students in this course. (Some University Physics problems will also be accessible to Principles of Physics students, though some will not.)
General College Physics students who wish to do so are welcome to work some or all of the University Physics questions and problems, though this is neither expected nor required. Many of the University Physics questions and problems are more challenging than those expected of General College Physics students, and a number of the problems require the use of calculus, which is not expected of General College Physics students.
You are not expected to submit these questions and problems. It would take too much of your time to key in all the answers and solutions. You should solve these problems and answer these questions in your notebook, in a form you can later reference and, if you later desire, revise. The Query at the end of the assignment will ask you selected questions, which you will at that time be expected to answer based on the work you have done in your notebook.
Remember that you are always welcome to ask questions at any time. Any question about a problem should include a copy of the problem and a summary of what you do and do not understand about it.
Questions related to q_a_
1. If a cart is found to have acceleration 30 cm/s^2 when it rolls freely down an incline having slope .05, and acceleration 70 cm/s^2 on an incline having slope .08, then
2. If a pendulum of length 30 cm goes through 54 cycles in a minute, then what is the corresponding estimate of the acceleration of gravity? If there is a 1% uncertainty in the count, then what is the uncertainty in the estimate?
Questions related to Introductory Problem Sets
These questions all relate to the figure below:
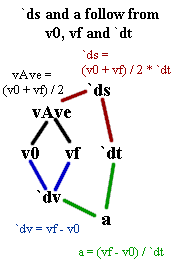
1. According to the figure, from what two quantities do we determine vAve?
According to the figure, from what two quantities do we determine `dv?
2. If we were to sketch a line from vAve to `dt, then the figure would contain a triangle with its vertices labeled vAve, `ds and `dt. This would indicate that there is a relationship among these three quantities which is dictated by at one or more of the following:
Answer the following:
3. If we were to sketch a line from `dv to `dt, then the figure would contain a triangle with its vertices labeled `dv, `ds and `dt. This would indicate that there is a relationship among these three quantities which is dictated by at one or more of the following:
Answer the following:
Questions/problems for Principles of Physics Students
The graph below depicts a trapezoid on a graph of v vs. t for some unspecified object. The questions that follow are related to this graph.
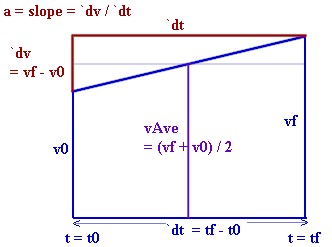
1. Sketch and label four trapezoids of your own:
Suppose that each trapezoid represents a runner. Describe what the runner is doing in each case, and how it differs from what he or she is doing in each of the other cases.
2. List the four trapezoids you sketched in the preceding problem, in each of the orders indicated below:
3. Identify the line segment in the depicted trapezoid whose length correspond to each of the following quantities:
4. In terms of the picture of the trapezoid, how do we construct the line segment for `dv?
In terms of the picture, how do we construct the line segment for vAve?
In terms of the picture, how do we construct a rectangle whose area is equal to that of the trapezoid?
In terms of the picture, how do we construct a triangle whose legs are `dv and `dt?
5. What are the height and width of the rectangle whose area is equal to that of the depicted trapezoid?
What is the meaning of the height?
What is the meaning of the width?
How are the height and width of a rectangle used to find its area?
6. What is the rise of the 'red' triangle in the figure (the 'red' triangle is the triangle having two red legs; its hypotenuse is blue)?
What is the run of that triangle?
What therefore is the slope of the triangle?
What does the rise of the triangle mean in terms of the motion of the object?
What does the run ise of the triangle mean in terms of the motion of the object?
What therefore does the slope of the triangle mean in terms of the motion of the object?
7. The slope of the trapezoid is (vf - v0) / (tf - t0), which could also have been written (vf - v0) / `dt.
8. The area of the trapezoid is (vf + v0) / 2 * ( tf - t0) = (vf + v0) / 2 * `dt. This represents the product of average velocity and time interval, i.e., the displacement.
Be prepared at any time to explain the meaning of the statement
Questions/problems for General College Physics Students
The figure shown under the heading 'Questions/problems for Principles of Physics Students' applies here as well.
1. What aspects of the figure are related to the definition of the average rate of change of position with respect to clock time, and how are they related?
2. What aspects of the figure are related to the definition of the average rate of change of velocity with respect to clock time, and how are they related?
3. How is it that we can assert that, for this graph, the average velocity is the average of the initial and final velocities?
4. Sketch an example of a velocity vs. clock time graph for a time interval, with the property that the average velocity on the interval is less than the average of the initial and final velocities. Be prepared to describe your sketch.
5. Derive the third and fourth equations of motion from the first two.
Questions/problems for University Physics Students
1. If the function s(t) = .3 m/s^3 * t^3 - 2 m/s^2 * t^2 + 5 m/s * t + 12 m, then:
2. Using the a(t) function you obtained in #1, integrate to find the general form of the v(t) and s(t) functions (you will obtain the general form if you include the integration constant with each integration; note that if you get two different integration constants you can't call them both 'c'; you might, for example, choose to call them c1 and c2).
Find the values of the integration constants required to fulfill the conditions v(0) = 4 m/s and s(0) = 20 m.
If one object moves according to the position function given in the first problem, and another moves according to the position function just obtained, how will the motions of the two objects compare?
3. If the acceleration of an object is constant, its initial velocity is v0 and its initial position is s0 we can find its velocity and position functions, in terms of a, v0, s0 and the clock time t.
Using integration, find the velocity function v(t) and the position function s(t):