011.  `query 11

 

Self-critique Rating:

Question:  `q set 3 problems 15-19.  Explain the difference between a conservative and a nonconservative force, and give an example of each.

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** A conservative force conserves energy--you can get your energy back. 

 

For example: 

 

Push something massive up a hill, then climb back down the hill.  The object, by virtue of its position, has the potential to return most of your energy to you, after regaining it as it rolls back down.  You will have done work against gravity as you move along a path up the hill, and gravity can return the energy as it follows its path back down the hill.  In this sense gravity conserves energy, and we call it a conservative force.

 

However, there is some friction involved--you do extra work against friction, which doesn't come back to you.  And some of the energy returned by gravity also gets lost to friction as the object rolls back down the hill.  This energy isn't conserved--it's nonconservative. **

 

Another more rigorous definition of a conservative force is that a force is conservative if the work done to get from one point to another independent of the path taken between those two points. 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qIf a system does work W1 against a nonconservative force while conservative forces do work W2 on the system, what are the change in the KE and PE of the system?  Explain your reasoning from a commonsense point of view, and include a simple example involving a rubber band, a weight, an incline and friction.

 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** `dKE is equal to the NET work done ON the system.

 

The KE of a system changes by an amount equal to the net work done on a system.

 

If work W1 is done BY the system against a nonconservative force then work -W1 is done ON the system by that force.

 

`dPE is the work done BY the system AGAINST conservative forces, and so is the negative of the work done ON the system BY nonconservative forces. 

`dPE = - W2.  PE decreases, thereby tending to increase KE.

So work -W1 is done ON the system by nonconservative forces and work W2 is done ON the system by a conservative force.

The KE of the system therefore changes by `dKE = -W1 + W2.

If the nonconservative force is friction and the conservative force is gravity, then since the system must do positive work against friction, W1 must be positive and hence the -W1 contribution to `dKE tends to decrease the KE. 

e.g., if the system does 50 J of work against friction, then there is 50 J less KE increase than if there was no friction.

If the work done by the conservative force on the system is positive,

e.g., gravity acting on an object which is falling downward, then since force and displacement in the same direction implies positive work, gravity does positive work and the tendency will be to increase the KE of the system and W2 would be positive. 

A couple of numerical examples:

If W2 is 150 J and W1 is 50 J, then in terms of the above example of a falling object, this would mean that gravity tends to increase the KE by 150 J but friction dissipates 50 J of that energy, so the change in KE will be only 100 J.  This is consistent with `dW_net_ON = -W1 + W2 = -50 J + 150 J = 100 J.

The previous example was of a falling object.  If the object was rising (e.g., a ball having been thrown upward but not yet at its highest point), displacement and gravitational force would be in opposite directions, and the work done by gravity would be negative. 

In this case W2 might be, say, -150 J.  Then `dKE would be -150 J - 50 J = -200 J. 

The object would lose 200 J of KE.  This would of course only be possible if it had at least 200 J of KE to lose.  For example, in order to lose 200 J of KE, the ball thrown upward would have to be moving upward fast enough that it has 200 J of KE.

STUDENT COMMENT

I find this really confusing. Could this be laid out in another way?

INSTRUCTOR RESPONSE

If you find this confusing at this point, you will have a lot of company.  This is a challenge for most students, and these ideas will occupy us for a number of assignments.   There is light at the end of the tunnel: It takes awhile, but once you understand these ideas, the basic ideas become pretty simple and even obvious, and once understood they are usually (but not always) fairly easy to apply

This could be laid out differently, but would probably be equally confusing to any given student. Different students will require clarification of different aspects of the situation.

If you tell me what you do and do not understand about the given solution, then I can clarify in a way that will make sense to you.

I also expect that in the process of answering subsequent questions, these ideas will become increasingly clear to you.

In any case feel free to insert your own interpretations, questions, etc. into a copy of this document (mark insertions with &&&& so I can locate them), and submit a copy.

STUDENT QUESTION

If the system goes against the force will this always make it negative?

INSTRUCTOR COMMENT

If a force and the displacement are in opposite directions, then the work done by that force is negative.

If the system moves in a direction opposite the force exerted BY the system, the work done BY the system is negative.

Note, however, that if this is the case then any equal and opposite force exerted ON the system will be in the direction of motion, so the force will do positive work ON the system.

A separate document related to this problem is located in the document

STUDENT COMMENT

This is a little confusing and I have read over the link that you gave. It will take some time to get use to the concepts.
So, almost all of the factors are equal and opposite of each other?

INSTRUCTOR COMMENT

In terms only of forces acting ON an object or system, we have the following:


1. The object or system can be subjected to any number of forces acting ON the system. The net force F_net_ON is the sum, the net effect, of all those forces.

2. On any given interval the work done by the net force is equal to the change in the KE of the object or system.

3. This is summarized in the work-kinetic energy theorem

`dW_net_ON = `dKE

4. Each force acting on the object or system can be classified as some combination of conservative and nonconservative forces, so

5. the net force can be expressed as the sum of a net conservative and a net nonconservative force:

F_net_ON = F_net_cons_ON + F_net_noncons_ON.

6. Thus `dW_net_ON = `dW_net_cons_ON + `dW_net_noncons_ON.

7. Change in PE can be defined to be equal and opposite the work done ON the system by conservative forces:

`dW_net_cons_ON = - `dPE

8. Since `dW_net_ON = `dW_net_cons_ON + `dW_net_noncons_ON, the work-kinetic energy theorem becomes

`dW_net_cons_ON + `dW_net_noncons_ON = `dKE.

9. Since `dW_net_noncons_ON = -`dPE this can be written

-`dPE + `dW_net_noncons_ON = `dKE.

10. This can be rearranged to

`dW_net_noncons_ON = `dKE + `dPE.

In the above we have explained the relationships among six quantities:

`dKE
F_net_ON
`dW_net_ON
`dW_net_ON_cons
`dW_net_ON_noncons
`dPE

The main relationships are

`dW_net_ON = `dKE and
`dW_net_ON_noncons = `dKE + `dPE.

If we replace the word ON by the word BY (indicating forces exerted and work done BY rather than ON the system), the force and therefore the work reverse sign.  In particular this gives us

`dKE + `dPE + `dW_net_BY_noncons = 0,

a form which is useful in understanding some problems.

For more practice, you may apply these principles to the suggested exercises at the link

query_11_suggested_exercise.htm
 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qIf the KE of an object changes by `dKE while the total nonconservative force does work `dW_nc on the object, by how much does the PE of the object change?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** We have `dKE + `dPE + `dWbyNoncons = 0:  The total of KE change of the system, PE change of the system and work done by the system against nonconservative forces is zero.

Regarding the object at the system, if W_nc is the work done ON the object by nonconservative forces then work -W_nc is done BY the object against nonconservative forces, and therefore `dWnoncons_on = -W_nc.

We therefore have `dKE + `dPE - W_nc = 0 so that `dPE = -`dKE + W_nc. **

Equivalently, the work-energy theorem can be stated

In this example the work done on the system by nonconservative forces is labeled W_nc, without the subscript ON and without the `d in front.  However it means the same thing, so the above becomes

W_nc = `dKE + `dPE

and we solve for `dPE to get

`dPE = -`dKE + W_nc

STUDENT COMMENT

 I’m still confused on how to understand when the energy is done on the object and when the energy is done against the object.

INSTRUCTOR RESPONSE

In an application, that can be the difficult question.

However in this case it is stated that W_nc is the work done by nonconservative forces ON the object.

STUDENT COMMENT:

I had the same logic as the given solution, however I got ‘dPE = -‘dKE – W_nc as the answer. I some how got an extra negative. Maybe Work can only be positive….??

INSTRUCTOR RESPONSE:

In this problem W_nc was specified as the work done on the object by nonconservative forces.

You have to be careful about whether W_nc is ON the system or BY the system.

You used the equation `dKE + `dPE + W_nc = 0; however that equation applies to the work done BY the system against nonconservative forces.  Written more specifically the equation you used would be

‘dKE + ‘dPE + W_nc_BY = 0 so

`dPE = - `dKE - `W_nc_BY.

W_nc_BY = - W_nc_ON so `dPE = - `dKE + W_nc_ON.

STUDENT RESPONSE WITH INSTRUCTOR'S COMMENTS (instructor comments in bold):

ok, so dke + dPe - W_nc = 0
W_nc is total nonconservative forces doing work on the object,

Right up to here

this increases kinetic energy and decreases potential energy.
 

there is no assumption about the sign of any of these quantities; any quantity could be positive or negative, as long as
`dKE + `dPE - `dW_nc_on = 0

If `dW_nc_ON is positive then `dPE + `dKE is positive, but this could occur with positive `dKE and `dPE, or with a negative `dPE with lesser magnitude than a positive `dKE, or with a negative `dKE with lesser magnitude than a positive `dPE. All you would know is that `dKE + `dPE would be positive.

If `dW_nc_ON is negative then `dPE + `dKE is negative, but this doesn't tell you anything about the sign of either of the two quantities.

All we can say is that `dPE = `dW_nc_on - `dKE.


Since it is decreasing the potential energy it is negative. dKE is the kinetic energy which is positive since the potential
energy is increased.

If `dW_nc_on = 0, for example, an increase in either KE or PE implies a decrease in the other. KE would increase due to a decrease in PE (e.g., if you drop an object), while an increase in PE would be associated with a decrease in KE (e.g., an object thrown upward gains PE as it loses KE).

So an increase in KE tends to decrease PE, though `dW_nc_on can be such that KE and PE both increase.

In this problem we solve for PE. So that dPE= - dKE + W_nc.
As potential energy increasess kinetic energy decreases and the non conservative work is positive because it is going with
the direction of force more so than against it.
 

An increase in PE could be the result of loss of KE and/or positive work done by nonconservative forces.

PE could also increase along with KE as long as `dW_nc_on is positive and large enough (e.g., a rocket increases both PE and KE due to nonconservative forces (the nonconservative forces result from ejecting fuel at high speed, i.e., from the rocket engines).
 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qGive a specific example of such a process.

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** For example suppose I lift an object weighing 50 N and in the process the total nonconservative force (my force and friction) does +300 J of work on the object while its KE changes by +200 J.  

More formally, `dW_noncons_ON = +300 J and `dKE = +200 J.  Since `dW_noncons_ON = `dKE + `dPE,  

So +300 J = +200 J + `dPE, and it follows that `dPE = +100 J.

STUDENT QUESTION (instructor responses inserted in bold)

&&&&&&I read your example first, and it makes no sense to me. Your force and the friction does 300J of work on the
object....
your force should be positive and friction should be negative right....so did you just add these two numbers together and
get a positve number???

Right.  No numbers were assumed for the work I do and the work done by friction.  These two forces make up the nonconservative force on the system, and we just assumed a single total.  If you wish you can assume, say, that I do 350 J of work and friction does -50 J.  However the breakdown of the individual nonconservative forces isn't the point here.  All we really need is the total work done on the object by nonconservative forces.

How did you know that is KE changed by 200J.....did you just make that up or did you mathmatically
figure that out???

The phrase starts with 'for example, then reads

'suppose I lift an object weighing 50 N and in the process the total nonconservative force (my force and friction) does +300 J of work on the object while its KE changes by +200 J'

So all these quantities are simply assumed, for the sake of a numerical example.

How does your 300J increase the KE by 200J??? I understand that if 'dKE is only 200J then the other
100J is 'dPE....I'm just not sure about the rest.

There is no specified connection between the 300 J of work I do and the 200 J of KE increase.  We just assume these quantities.  Once we have these quantities (in this case, simply by assumption; in other problems we will often find these quantities from other information), they dictate the PE increase.

There are a number of ways to think about this intuitively.  For example:

&&&&&

STUDENT COMMENT

The problem didn’t seem to fit the equation we got earlier. This stuff is very confusing. I am going to read over it again.

<h3>Your example is good.

You previously reasoned from the equation

`dPE + `dKE + `dW_by_NC = 0,

obtaining `dPE = - `dKE - `dW_by_NC.

In your example you assumed that friction does 100 J of work on the box, and `dKE = 50 J. It would follow that the work done by the box against friction is -100 J; i.e., `dW_ON_nc = 100 J so `dW_by_nc = -100 J.

Thus in your example `dPE = - `dKE - `dW_by_NC. = - 50 J - (-100 J) = +50 J.

This is the result you obtained; however in your equation you used _by_ where you should have used _on_, so be sure you understand the distinction.  Since 'on' and 'by' are opposite, - `dKE - `dW_by_NC = -`dKE + `dW_on_NC.

You could as well have reasoned from the equation

`dW_nc_ON = `dPE + `dKE,

which leads to

`dPE = `dW_nc_ON - `dKE.

You assumed frictional work on the system to be 100 J, so `dW_nc_ON = 100 J. This leads to

`dPE = `dW_nc_ON - `dKE.= 100 J - 50 J = 50 J,

the same result obtained previously.

Since `dW_nc_ON = - `dW_nc_by, the two equations used in this instructor response are equivalent:

`dPE + `dKE + `dW_nc_by = 0 is completely equivalent to
`dW_nc_ON = `dPE + `dKE.

Either equation, properly applied, leads to the correct result.</h3>

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qClass notes #10.

Why does it make sense that the work done by gravity on a set of identical hanging washers should be proportional to the product of the number of washers and the distance through which they fall? Why is this consistent with the idea that the work done on a given cart on an incline is proportional to the vertical distance through which the cart is raised?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** Informally:

More formally, the force exerted by gravity is the same on each clip, so the total gravitational force on the hanging clips is proportional to the number of clips.  The work done is the product of the force and the displacement in the direction of the force, so the work done is proportional to product of the number of washers and the vertical displacement.

 

To pull the cart up a slope at constant velocity the number of washers required is proportional to the slope (for small slopes), and the vertical distance through which the cart is raised by a given distance of descent is proportional to the slope, to the work done is proportional to the vertical distance thru which the cart is raised. **

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qHow does the work done against friction of the cart-incline-pulley-washer system compare with the work done by gravity on the washers and the work done to raise the cart?   Which is greatest?  What is the relationship among the three?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** The force exerted by gravity on the hanging weights tends to move the system up the incline.  The force exerted by gravity on the cart has a component perpendicular to the incline and a component down the incline, and the force exerted by friction is opposed to the motion of the system.

 

In order for the cart to move with constant velocity up the incline the net force must be zero (constant velocity implies zero accel implies zero net force) so the force exerted by gravity in the positive direction must be equal and opposite to the sum of the other two forces.  So the force exerted by gravity on the hanging weights is greater than either of the opposing forces.

 

So the force exerted by friction is less than that exerted by gravity on the washers, and since these forces act through the same distance the work done against friction is less than the work done by gravity on the washers.

 

The work done against gravity to raise the cart is also less than the work done by gravity on the washers. 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qWhat is our evidence  that the acceleration of the cart is proportional to the net force on the cart?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

The net force is the sum of the gravitational force on the weights, and the frictional force (one force being positive, the other negative).

The acceleration is the net force divided by total mass (mass of cart plus hanger plus washers).

Washers are progressively transferred from the cart to the hanger, which keeps the mass of the system constant while increasing the net force. So the acceleration increases with the number of washers on the hanger.

The gravitational force on the weights is therefore proportional to the number of washers on the hanger.

However the acceleration is not proportional to the number of weights.

STUDENT COMMENT

I did not go into this great of detail. I simply used the one equation. Is this necessary to go in this thoroughly or was this just for our
knowledge?

INSTRUCTOR RESPONSE

The question is asking about 'our evidence'.

The fact that the law has been thoroughly tested by centuries of engineering and physics is what makes it a law, but the question here is whether the evidence obtained in the experiment (in the Class Notes) indicates that the acceleration of this particular cart is proportional to the net force acting on it.

Of course our experiments had better agree with the law, within their limits of precision. Our results will be more a test of our experimental design, and our execution of that design, than a test of the established law.

The law itself turns out to be valid only within certain restrictions, becoming invalid at relativistic velocities and at the quantum level of matter (realms far beyond our everyday experience and perception of the world).

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

 

Question:  Calculate the displacement and velocity at times of (a) 0.500, (b) 1.00, (c) 1.50, and (d) 2.00 s for a ball thrown straight up with an initial velocity of 15.0 m/s. Take the point of release to be y_0 = 0 .

With the number of significant figures specified for this problem we would need to use a 3-significant-figure acceleration.  However the acceleration at different points on the surface of the Earth varies in the third significant figure.  Since the location isn't specified, the solution given here will ignore significant figures and use the value 10 m/s^2 for the acceleration of gravity and time intervals .5, 1, 1.5 and 2 s.  You should be aware of the significant-figure implications both of the given information and the assumptions used this given solution.

The acceleration of gravity is 10 m/s^2 downward.  We understand the meaning of this acceleration to be that the speed of the object changes by 10 m/s every second, and that the velocity change is in the downward direction.

It isn't explicitly stated, but it can be taken as implicit that the given times are in fact the times as measured on a running clock which reads 0 at the instant of release.

Directly reasoned solution for clock time 0.5 second:

In 0.5 second the change in speed will therefore be 5 m/s (if the change is 10 m/s every second, then in half a second it will be half of 10 m/s or 5 m/s).  The velocity change is in the downward direction, so an initial upward speed of 15 m/s will in this time reduce to 10 m/s.

During the 0.5 second interval, then, the velocity changes from 15 m/s to 10 m/s.  The average velocity, since acceleration is uniform (so that the v vs. t graph is a straight line) is therefore 12.5 m/s. 

In 0.5 second with average velocity 12.5 m/s, the object will therefore move through displacement `dy = 12.5 m/s * 0.5 second = 6.75 meters.

So after 0.5 second, the object's vertical position will be y = y_0 + 6.75 meters = 0 + 6.75 meters = 6.75 meters.

Similar reasoning for the other given clock times leads to the following conclusions.  Each line corresponds to the interval from clock time 0 to the given clock time.

clock time change in velocity initial velocity final velocity ave velocity position
0.5 -5 m/s 15 m/s 10 m/s 12.5 m/s 6.75 m
1 -10 m/s 15 m/s 5 m/s 10 m/s 10 m
1.5 -15 m/s 15 m/s 0 m/s 7.5 m/s 11.25 m
2 -20 m/s 15 m/s -5 m/s 5 m/s 10 m
           


More generally we could reason out the position at clock time t as follows:

Taking upward as the positive direction, the acceleration being downward is negative, with value -10 m/s^2.

The change in velocity for the interval from clock time 0 to clock time t is therefore -10 m/s^2 * t.

The final velocity for this interval is thus 15 m/s - 10 m/s^2 * t.

The average velocity for the interval is the average of the initial and final velocities, so vAve = (15 m/s + (15 m/s - 10 m/s^2 * t) ) / 2 = 15 m/s - 10 m/s^2 * t / 2 = 15 m/s - 5 m/s^2 * t.

The displacement during the interval is thus `dy = vAve * `dt = vAve * (t - 0 s) = (15 m/s - 5 m/s^2 * t) * t = 15 m/s * t - 5 m/s^2 * t^2.

Evaluating this for t = .5 s, 1 s, 1.5 s and 2 s we obtain respective displacements 6.75 m, 10 m, 11.25 m and 10 m.

The above solutions provide insight into the nature of the motion that can be bypassed by using the third equation of motion `ds = v0 `dt * 1/2 a `dt^2.  It isn't a good idea to bypass insights, so you should be able to reason out the solution in the above ways, but it's also important to be able to use the equations.  And once you're comfortable with the reasoning process, the equations often provide the quickest path to the solution:

Plugging t = 0, 0.5, 1, 1.5 and 2 into the equation we obtain respective displacements 6.75 m, 10 m, 11.25 m and 10 m.

If the displacements are added to the initial position y_0 = 0 we obtain the desired heights, which are not surprisingly identical to those obtained previously. 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating:

Given Solution: 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

 

Question:  `qprin phy and gen phy prob 34:  Car rolls off edge of cliff; how long to reach 85 km/hr?

 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`aWe know that the acceleration of gravity is 9.8 m/s^2, and this is the rate at which the velocity of the car changes.  The units of 85 km/hr are not compatible with the units m/s^2, so we convert this velocity to m/s, obtaining velocity

Common sense tells us that with velocity changing at 9.8 m/s every second, it will take between 2 and 3 seconds to reach 23.6 m/s. 

More precisely, the car's initial vertical velocity is zero, so using the downward direction as positive, its change in velocity is `dv = 23.6 m/s. 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `q****   prin phy and gen phy  problem 2.52 car 0-50 m/s in 50 s by graph

How far did the car travel while in 4 th gear and how did you get the result?

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a**  In 4th gear the car's velocity goes from about 36.5 m/s to 45 m/s, between clock times 16 s and 27.5 s.

 

Its average velocity on that interval will therefore be

 

vAve = (36.5 m/s  +  45 m/s) / 2 = 40.75 m/s and the time interval is

'dt =  (27.5s - 16s) = 11.5 s.

 

We therefore have

'ds = vAve * `dt = 40.75 m/s * 11.5 s = 468.63 m.

 

The area under the curve is the displacement of the car, since vAve is represented by the average height of the graph and `dt by its width.  It follows that the area is vAve*'dt, which is the displacement `ds.

 

The slope of the graph is the acceleration of the car. This is because slope is rise/run, in this case that is 'dv/'dt, which is the ave rate of change of velocity or acceleration.

 

We already know `dt, and we have `dv = 45 m/s - 36.5 m/s = 8.5 m/s.

 

The acceleration is therefore

 

a = `dv / `dt = (8.5 m/s) / (11.5 s) = .77 m/s^2, approx. **

 

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question: A powerful motorcycle can accelerate from rest to 26.8 m/s (100 km/h) in only 3.90 s. (a) What is its average acceleration? (b) How far does it travel in that time?

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

Acceleration is defined to be the rate of change of velocity with respect to clock time.

By the definition of rate of change, then, average acceleration = (change in velocity) / (change in clock time).

In this example velocity changes by 26.8 m/s as clock time changes by 3.9 s, so

average acceleration = 26.8 m/s / (3.9 s) = 7 m/s^2, approximately.

If the acceleration remains uniform (which will not actually be the case) the average velocity for the 3.9 s interval will be the average of the initial and final velocities, so

average velocity = (0 m/s + 26.8 m/s) = 13.4 m/s.

At this average velocity, in 3.9 s the displacement of the motorcycle will be

13.4 m/s * 3.9 s = 50 meters, approximately.

 

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:



Question: Calculate the displacement and velocity at times of (a) 0.500, (b) 1.00, (c) 1.50, (d) 2.00, and (e) 2.50 s for a rock thrown straight down with an initial velocity of 14.0 m/s from the Verrazano Narrows Bridge in New York City. The roadway of this bridge is 70.0 m above the water.

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

Your solution will have used 9.8 m/s^2 as the acceleration of gravity.  The solution given here is for rough comparison, and uses the rounded-up acceleration 10 m/s^2.

Using 10 m/s^2 downward for the acceleration of gravity, the changes in velocity of the rock will all be downward, and will have magnitudes

`dv = 5 m/s in .5 sec

`dv = 10 m/s in 1 sec

`dv = 15 m/s in 1.5 sec

`dv = 20 m/s in 2 sec

`dv = 25 m/s in 2.5 sec.

Given the downward initial velocity of 14 m/s, the rock will attain downward velocities of

19 m/s in .5 sec

24 m/s in 1 sec

29 m/s in 1.5 sec

34 m/s in 2 sec

39 m/s in 2.5 sec.

(Note: It should be clear from these numbers that a graph of velocity vs. clock time is linear, with downward velocity increasing by 5 m/s every .5 sec).

For each interval the average velocity will be the average of the 14 m/s initial velocity and the final velocity attained during that interval.  For example during the first interval the initial velocity is 14 m/s and the final velocity is 19 m/s, so the average velocity for this interval is (14 m/s + 19 m/s) / 2 = 16.5 m/s.  Thus in the .5 sec interval the rock with travel 16.5 m/s * .5 sec = 8.25 m.

For the other intervals we find the following:

average velocity (14 m/s + 24 m/s) = 19 m/s for 1 sec, so displacement is 19 m/s * 1 s = 19 m

average velocity (14 m/s + 29 m/s) = 21.5 m/s for 1.5 sec, so displacement is 21.5 m/s * 1.5 s = 31.75 m

average velocity (14 m/s + 34 m/s) = 24 m/s for 2 sec, so displacement is 24 m/s * 2 s = 48 m

average velocity (14 m/s + 39 m/s) = 26.5 m/s for 2.5 sec, so displacement is 26.5 m/s * 2.5 s = 66.25 m

(Note:  It should be immediately clear from these results that a graph of downward velocity vs. clock time is increasing at an increasing rate).

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:



Question: A steel ball is dropped onto a hard floor from a height of 1.50 m and rebounds to a height of 1.45 m. (a) Calculate its velocity just before it strikes the floor. (b) Calculate its velocity just after it leaves the floor on its way back up. (c) Calculate its acceleration during contact with the floor if that contact lasts 0.0800 ms (8.00×10−5 s) . (d) How much did the ball compress during its collision with the floor, assuming the floor is absolutely rigid?

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

Using the equation vf^2 = v0^2 + 2 a `ds, with downward as the positive direction, v0 = 0, a = 10 m/s^2 and `ds = 1.5 m, we obtain

vf^2 = 0 ^2 + 2 * 10 m/s^2 * 1.5 m = 30 m^2 / s^2

vf = +- sqrt( 30 m^2 / s^2) = +- sqrt( 30 m^2 / s^2) = +- 5.5 m/s.

The ball therefore strikes the floor at 5.5 m/s.  The velocity is in the positive direction (recall that the positive direction was chosen as downward; had upward been chosen as the positive direction the velocity would have been -5.5 m/s).

Using the same equation, with downward still the positive direction, to analyze the upward motion we have vf = 0 (the ball comes to rest, at least for an instant, at height 1.45 m), a = 10 m/s^2, and `ds = -1.45 m (the displacement is upward and for this given solution downward has been chosen as the positive direction).

The solution to the equation vf^2 = v0^2 + 2 a `ds for v0 is

v0 = +- sqrt( vf^2 - 2 a `ds).

Substituting the values of vf, a and `ds we get

v0 = +- sqrt( 29 m/s) = +- 5.4 m/s.  Knowing that v0 is upward, hence negative, we get v0 = - 5.4 m/s.

So the ball strikes the floor at +5.5 m/s and rebounds at -5.4 m/s.  For the interval between first and last contact with the floor, then we have

v0 = 5.5 m/s, vf = -5.4 m/s and `dt = 8 * 10^-5 s.

The change in velocity is therefore -10.9 m/s (this can be calculated without much understanding as `dv = vf - v0 = -5.4 m/s - 5.5 m/s = -10.9 m/s; it can be understood by noting that the ball has to lose 5.5 m/s of velocity to come to rest for an instant, which entails a change of -5.5 m/s, then has to change by an additional -5.4 m/s to achieve the -5.4 m/s final velocity, so that the total change in velocity is -10.9 m/s).

This change in velocity takes place during an interval of 8 * 10^-5 s so the average acceleration is

average acceleration = (change in velocity) / (change in clock time) = -10.9 m/s / (8 * 10^-5 s) = -1.4 * 10^5 m/s^2, approx..

(Note:  actual acceleration is not uniform, and the maximum acceleration is significantly greater than that calculated here).

To find the approximate compression of the ball we can assume that it came to rest from 5.5 m/s in half the time, 4 * 10^-5 s.  This gives us v0, vf and `dt for the interval between first contact and coming to rest, and it is straightforward to calculate the displacement `ds.  Assuming that the floor is rigid, the displacement is accounted for by the compression of the ball.  The result is on the order of 10^-4 meter. 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  Use the graph below to find the velocity at t = 10 seconds.

 

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

From the graph it appears that the position changes linearly from about 2.5 m to 5 m in an interval that runs from 0 seconds to 11 seconds.  Since the graph appears to be linear for this interval, the average velocity for the entire interval should apply at t = 10 seconds.

The average velocity for the interval is

average velocity = (change in position) / (change in clock time) = (5 m - 2.5 m) / (11 sec - 0 sec) = 2.5 m / (11 sec) = .23 m/s, approx..

It should be clear that this calculation corresponds to the calculation of the slope of the line from (0 sec, 2.5 m) to (11 sec, 5 m), with the numerator corresponding to the rise and the denominator to the run.

 

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question: A bullet in a gun is accelerated from the firing chamber to the end of the barrel at an average rate of 6.20×10^5 m/s^2 for 8.10×10−4 s . What is its muzzle velocity (that is, its final velocity)?

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:  

average acceleration = (change in velocity) / (change in clock time) so

(change in velocity) = average acceleration * change in clock time = 6.2 * 10^5 m/s^2 * 8.1 * 10^-4 s = 5 * 10^2 m/s, approx..  This is about 500 m/s.

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  (a) A world record was set for the men’s 100-m dash in the 2008 Olympic Games in Beijing by Usain Bolt of Jamaica. Bolt “coasted” across the finish line with a time of 9.69 s. If we assume that Bolt accelerated for 3.00 s to reach his maximum speed, and maintained that speed for the rest of the race, calculate his maximum speed and his acceleration. (b) During the same Olympics, Bolt also set the world record in the 200-m dash with a time of 19.30 s. Using the same assumptions as for the 100-m dash, what was his maximum speed for this race?

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

We assume that Bolt accelerated uniformly for 3 seconds, then ran at the speed he achieved for another 6.69 seconds, covering 100 meters in the process.

What we don't know is his acceleration, so we will set up the situation with acceleration a as the unknown.

During the 3 second acceleration Bolt would have started from rest, reaching a speed of

vf = (3 seconds) * a. 

His average speed would have been

vAve = (0 m/s + 3 seconds * a) / 2 = 1.5 seconds * a

and he would have covered a distance of

`ds_1 = vAve * 3 seconds = 1.5 seconds * a * 3 seconds = a * 4.5 sec^2.

He would have then run at velocity vf for an additional 6.69 seconds, covering a distance of

`ds_2 = vf * 6.69 sec = 3 sec * a * 6.69 sec = a * 20.07 sec^2.

The total distance is 100 meters, which is equal to `ds_1 + `ds_2, so

a * 4.5 sec^2 + a * 20.07 sec^2 = 100 meters.

We easily solve for a, obtaining

a = 100 meters / (24.57 sec^2) = 4.07 m/s^2.

From this we find that his final velocity would have been

vf = a * 3 sec = 12.21 m/s.

 

His acceleration, however, would not have been uniform, so this estimate will not be completely accurate.  In fact, his maximum speed (obtained by timing him between the 60 m and 80 m marks) was found to be about 12.4 m/s.  However our estimate of 12.21 m/s is pretty close.

(additional note:  in 2009 Bolt lowered the 100 meter record to 9.57 m/s and the 200 meter record to 9.19 s)

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

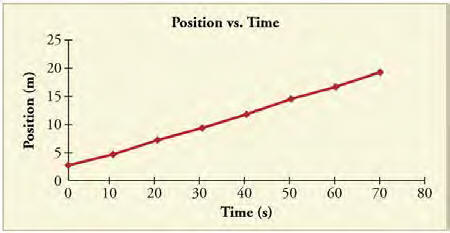
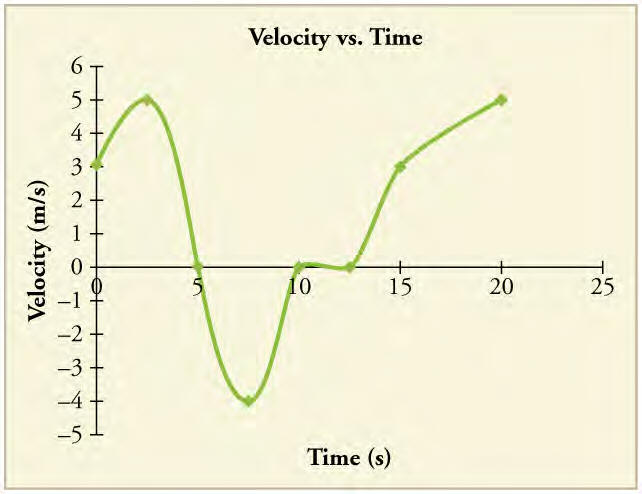
Question: (a) Use the slope of the curve in Figure 2.64 to find the jogger’s velocity at t = 2.5 s . (b) Repeat at 7.5 s. These values must be consistent with the graph in Figure 2.65.

Your solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

 

Given Solution:

The slope of the position vs. time graph appears to be nearly constant for the first 2.5 seconds.  The rise for this interval is 10 m and the run is 2.5 sec, so the slope, which represents the velocity, is 10 m / (2.5 s) = 4 m/s.  The graph of v vs. t shows a velocity of 5 m/s at t = 2.5 s, but the difference can be attributed to the difficulty of estimating intervals of linearity.  The thickness of the lines and other flaws of the graph make it impossible to construct an accurate tangent line, though it would still be worthwhile to do so.

Between t = 5 and t = 7.5 seconds the graph appears to be nearly, but not quite, linear.  The average slope between the two corresponding points of the graph appears to be about -7.5 meters / (2.5 seconds) = -3 m/s, but the graph is steeper than this average slope at t = 7.5 sec, so an estimate of -3.5 m/s could be reasonable.  The v vs. t graph indicates a velocity of -4 m/s at t = 7.5 sec, so there is reasonable consistency.

 

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

 

Question:  `q ****   Gen phy   what is the meaning of the slope of the graph and why should it have this meaning?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** The graph is of velocity vs. clock time, so the rise will be change in velocity and the run will be change in clock time.  So the slope = rise/run represents change in vel / change in clock time, which is acceleration. **

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qGen phy   what is the meaning of the area under the curve, and why does it have this meaning?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** The area under the curve is the distance traveled. This is so because 'ds = vAve*'dt.

 

'dt is equal to the width of the section under the curve and vAve is equal to the average height of the curve. The area of a trapezoid is width times average height. Although this is not a trapezoid it's close enough that we for the purpose of estimation can analyze it as such.

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `qGen phy   what is the area of a rectangle on the graph and what does it represent?

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** The area of a rectangle on the graph represents a distance. **

 

 

 

Self-critique (if necessary):

 

 

 

 

 

 

 

 

 

 

Self-critique Rating:

Question:  `quniv phy  problem 2.90 from 10th edition (University Physics students should solve this problem now).  Superman stands on the top of a skyscraper 180 m high.  A student with a stopwatch, determined to test the acceleration of gravity for himself, steps off the top of the building but Superman can't start after him for 5 seconds.  If Superman then propels himself downward with some init vel v0 and after that falls freely, what is the minimum value of v0 so that he catches the student before that person strikes the ground?

`quniv phy   what is Superman's initial velocity, and what does the graph look like (be specific)?

 

 

Your Solution:

 

 

 

 

 

 

 

 

 

 

Confidence Rating:

Given Solution: 

`a** In time interval `dt after leaving the building the falling student has fallen through displacement `ds = v0 `dt + .5 a `dt^2, where v0 = 0 and, choosing the downward direction to be positive, we have a = -9.8 m/s^2.  If `ds = -180 m then we have `ds = .5 a `dt^2 and `dt = sqrt(2 * `ds / a) = sqrt(2 * -180 m / (-9.8 m/s^2)) = 6 sec, approx..

 

Superman starts 5 seconds later, and has 1 second to reach the person. Superman must therefore accelerate at -9.8 m/s^2 thru `ds = -180 m in 1 second, starting at velocity v0.

 

Given `ds, `dt and a we find v0 by solving `ds = v0 `dt + .5 a `dt^2 for v0, obtaining v0 = (`ds - .5 a `dt^2) / `dt = (-180 m - .5 * -9.8 m/s^2 * (1 sec)^2 ) / (1 sec) = -175 m/s, approx.

 

Note that Superman's velocity has only about 1 second to change, so changes by only about -9.8 m/s^2, or about -10 m/s^2. **

 

``qsketch a graph of Superman's position vs. clock time, and on the same graph show the student's position vs. clock time, with clock time starting when the person begins falling

 

 

Your solution: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Confidence rating::

Given Solution: 

`a** If we start our clock at t = 0 at the instant the student leaves the top of the building then at clock time t the student's `dt will be just equal to t and his position will be x = x0 + v0 t + .5 a t^2 = .5 a t^2, with x0 = 180 m and a = -9.8 m/s^2.  A graph of x vs. t will be a parabola with vertex at (0,180), intercepting the t axis at about t = 6 sec.

 

For Superman the time of fall will be `dt = t - 5 sec and his position will be x = x0 + v0 (t-5sec) + .5 a (t-5sec)^2, another parabola with an unspecified vertex.

 

A graph of altitude vs. t shows the student's position as a parabola with vertex (0, 180), concave downward to intercept the t axis at (6,0).  Superman's graph starts at (5,180) and forms a nearly straight line, intercepting the t axis also at (6,0).  Superman's graph is in fact slightly concave downward, starting with slope -175 and ending with slope -185, approx. **

 

 

Self-critique (if necessary):

 

Self-critique Rating:

 

 

 

 

 

 

 

STUDENT QUESTIONS

I am not clear about the relationship between KE,  PE and Work

Will nonconservative forces always be - ?

And my notes say PE can never be neg. therefore PE will always be conserved?

INSTRUCTOR RESPONSE

Any force can do positive or negative work, depending on how the direction of the force compares to the direction of the displacement.

To determine the sign of a force or a displacement, you first to choose your positive direction.  The choice is yours.  Having made that choice:

KE = 1/2 m v^2. v^2 can't be negative, nor can m, so KE can't be negative.

PE can be positive or negative.

`dKE represents change in KE on an interval, and can be positive or negative
`dPE represents change in PE on an interval, and can be positive or negative.

Here is a summary of the work-energy theorem:

The work-kinetic energy theorem tells us that

where `dW_Net_ON is the work done by the net force acting on the system.

`dW_net_ON = `dW_nc_ON + `dW_cons_ON (work by the net force acting on the system is broken into work done by the conservative and nonconservative forces acting on the system)

`dW_cons_ON = -`dPE (change in PE is the result of conservative forces acting on the system, and is equal and opposite to the work done by those forces)

These ideas are combined to give us