If your solution to stated problem does not match the given solution, you should self-critique per instructions at http://vhcc2.vhcc.edu/dsmith/geninfo/labrynth_created_fall_05/levl1_22/levl2_81/file3_259.htm.
Your solution, attempt at solution. If you are unable to attempt a solution, give a phrase-by-phrase interpretation of the problem along with a statement of what you do or do not understand about it. This response should be given, based on the work you did in completing the assignment, before you look at the given solution.
033. `query 33
Question: `qQuery modeling simple harmonic motion with a reference circle.
In what sense can we say that the motion of a pendulum is modeled by the motion of a point moving at constant velocity around a reference circle? Be specific.
Your solution:
Confidence rating::
Given Solution:
`aGOOD STUDENT ANSWER:
A point moving around a circle can be represented by two perpendicular lines whose intersection is that point of constant velocity. The vertical line then is one that moves back and forth, which can be synchronized to the oscillation of the pendulum.
The figure below depicts the reference circle. The vector from the origin to the circle is called the radial vector. The tip of this vector is on the circle, as is called the reference point. A vertical line through the reference point extends down to the x axis, and a horizontal line through the reference point extends over to the y axis. The points where these lines meet the axes are the x and y coordinates of the reference point.
As the reference point and the radial vector move around the circle, the x and y coordinates change. If the reference point is moving counterclockwise around the circle, then starting from the position shown in the figure, the x coordinate will decrease. We imagine an object which moves in such a way that its x coordinate coincides with that of the reference point; in this sense the object 'tracks' the reference point as the object moves along the x axis.
When the reference point reaches the y axis its x coordinate will be zero.
When the reference point reaches the negative x axis the x coordinate will be at its extreme value, i.e., a point as far from the origin as possible for a point moving around this circle.
As the reference point continues moving around the circle an object tracking its x coordinate begins to move to the right, slowly at first them more and more quickly as it approaches the origin.
The x coordinate is again 0 when the reference point reaches the negative y axis. At that point the object has its maximum speed.
As the reference point approaches the positive x axis the x coordinate changes more and more slowly, reaching an extreme point when the reference point reaches the positive x axis.
Thus as the reference point continues to move around the circle, the object will continue to oscillate back and forth along the x axis.
An object which moves in this manner is said to be undergoing simple harmonic motion.
A simple pendulum, oscillating freely with an amplitude much less than its length, is modeled in this manner by a reference circle whose radius is equal to its amplitude of motion.
The time required for one complete trip around the reference circle corresponds to the period of the pendulum (i.e., to the time required for one complete oscillation of the pendulum).
Self-critique (if necessary):
Self-critique Rating:
Question: At what point(s) in the motion a pendulum is(are) its velocity 0?
Your solution:
Confidence rating::
Given Solution:
GOOD STUDENT ANSWER:
The pendulum has two points of v= 0. One at each end as it
briefly comes to a stop to
PARTIALLY CORRECT STUDENT ANSWER: equilibrium, and at each
extreme points of the oscillation, because the pendulum briefly stops at these
points
INSTRUCTOR COMMENT: If a pendulum is not swinging, then its velocity at
the equilibrium position is zero.
However if, as in the present case, it is swinging, then its passes thru the
equilibrium position with a nonzero velocity.
Furthermore its velocity as it passes through equilibrium is the maximum velocity it attains during its motion.
Question: At what point(s) in the motionof a pendulum is(are) its speed a maximum?
Your solution:
Confidence rating::
The pendulum swings from one extreme point to the other, then back, repeating this motion again and again.
Halfway between the extreme points is the equilibrium point, the point at which the pendulum would naturally hang if it wasn't moving.
It is at this halfway point that the pendulum reaches its maximum velocity.
-
As we will see, it is at the equilibrium position, and only at the equilibrium position, where the velocity of the pendulum is equal to the velocity of the point on the reference circle.
-
This could be reasoned out from energy considerations. The equilibrium position is the position at which the pendulum's mass is lowest, and so it the point at which its gravitational potential energy is lowest. Assuming that no nonconservative forces act on the pendulum, this is the point at which its kinetic energy is therefore highest.
GOOD STUDENT ANSWER:
The mid point velocity of the pendulum represents its greatest speed since it begins at a point of zero and accelerates by gravity downward to equilibrium, where it then works against gravity to finish the oscillation.
GOOD STUDENT DESCRIPTION OF THE FEELING: At the top of flight, the pendulum 'stops' then starts back the other way. I remember that I used to love swinging at the park, and those large, long swings gave me such a wonderful feeling at those points where I seemed to stop mid-air and pause a fraction of a moment. Then there was that glorious fall back to earth. Too bad it makes me sick now. That was how I used to forget all my troubles--go for a swing.
*&*& INSTRUCTOR COMMENT: That extreme point is the point of maximum acceleration. **
STUDENT QUESTION
I thought that the equilibrium point was where the velocity
was at zero??? Is this also where the pendulum reaches its
maximum velocity??? I figured that it would be gaining the most speed as it went
from a zero velocity and was released-
maybe when it leaves the amplitude point?
INSTRUCTOR RESPONSE
The equilibrium point is the point at which the pendulum naturally hangs while stationary.
When it's moving, the equilibrium point is still the point at which the pendulum would naturally hang if it was stationary. For a moving pendulum that point coincides with the 'low point' of its arc.
I refer to the points where velocity is for an instant zero as the 'extreme points' of its motion. At these points its distance from the equilibrium position is equal to its amplitude.
The pendulum does speed up most quickly when it begins its swing back from its equilibrium point.
Self-critique (if necessary):
Self-critique Rating:
Question:
`qHow does the maximum speed of the pendulum compare with the speed of the point on the reference circle?
Your solution:
Confidence rating::
Given Solution:
`a** At the equilibrium point the pendulum is moving in the same direction and with the same speed as the point on the reference circle. At any other point it is moving more slowly.
University Physics Note:
You can find the average speed by integrating the speed function, which is the absolute value of the velocity function, over a period and then dividing by the period (recall from calculus that the average value of a function over an interval is the integral divided by the length of the interval).
You find rms speed by finding the average value of the squared velocity and taking the square root (this is the meaning of rms, or root-mean-square). **
STUDENT QUESTION: what about at any point other than
equilibrium, will the speed hold the same as for a circle where speed closest to
the reference point is slower than at the radius
INSTRUCTOR RESPONSE: The point on the reference circle has constant speed.
Unless the reference point is moving in the same direction as the pendulum, the
part of its speed in the direction of the pendulum's motion is less than its
speed on the reference circle.
Thus, at only two points on the reference circle is the speed of the pendulum as
great at the speed of the reference point. Those points coincide with the
equilibrium position of the pendulum (i.e., at the equilibrium position the
motion of the reference-circle point is in the same direction as that of the
pendulum).
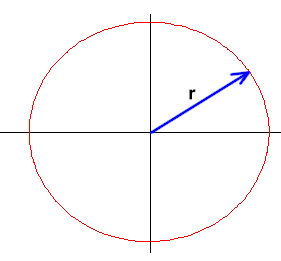
The figure below depicts the reference circle along with the radial vector r , the vector from the center of the circle to the reference point. This particular vector corresponds to an angular position of about 35 degrees.
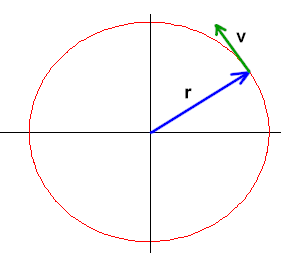
The next figure depicts as well the velocity vector v for the reference point, assuming that the reference point is moving in the counterclockwise direction. The velocity of the reference point is tangent to the circle, and hence perpendicular to the radial vector.
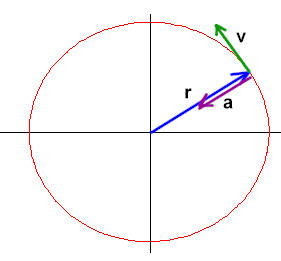
The final figure adds the centripetal acceleration vector a , which points back along the radial vector toward the origin. In the figure the acceleration vector is slightly offset from the radial vector, to make it clearly visible. In reality this vector would lie right over the radial vector.
If this figure models the motion of an object oscillating back and forth along the x axis, then the velocity of the object corresponds to the x component of v. It is clear that in this picture the x component of v is of lesser magnitude than v. That is, the object is moving more slowly than the reference point.
If the radial vector was horizontal, then the velocity v of the reference point would be vertical and its x component would be zero. The object would at that instant be stationary.
If the radial vector was vertical, then the velocity v of the reference point would be horizontal, and its x component would be of the same magnitude as v. The object would be moving at the same speed as the reference point and this would be its maximum speed.
Self-critique (if necessary):
Self-critique Rating:
Question: `qHow can we determine the centripetal acceleration of the point on the reference circle?
Your solution:
Confidence rating::
Given Solution:
`a** Centripetal acceleration is v^2 / r. Find the velocity of a point on the reference circle (velocity = angular velocity * radius).
The acceleration of the actual pendulum (which we assume moves along the x axis) is the x component of the centripetal acceleration of the reference point.
-
When the pendulum is at one of its extreme positions, the reference circle is on the x axis and the centripetal acceleration vector points back along the x axis toward the origin, so at this point the acceleration of the pendulum is equal to the centripetal acceleration of the reference point.
-
When the pendulum is at its equilibrium position the reference point lies directly above or below the pendulum, with its centripetal acceleration vector pointing in the vertical direction. The centripetal acceleration vector therefore has no component in the direction of the pendulum's motion, and the pendulum is for that instant not accelerating.
-
At any other position the centripetal force vector has a nonzero component in the x direction which has a magnitude less than that of the vector. This component is identical to the acceleration of the pendulum.**
If we want to find the centripetal acceleration of a circle
we can use the formula a_cent= v^2/r
The only thing I wonder about is if we would know what the radius of the circle
is or is there a formula we could use to
solve for this?
INSTRUCTOR RESPONSE
The radius of the reference circle is equal to the amplitude of motion.
When a pendulum moving along the x axis it at its maximum position x = A, the reference point is passing through the positive x axis, and the r vector is directed along the x axis. Thus the magnitude of the r vector is equal to the amplitude A, and the radius of the circle is therefore equal to the amplitude.
Self-critique (if necessary):
Self-critique Rating:
Question: `qQuery gen phy problem 9.12 30 kg light supported by wires at 37 deg and 53 deg with horiz.
What is the tension in the wire at 37 degrees, and what is the tension in the other wire?
Your solution:
Confidence rating::
Given Solution:
`a** The given solution is for a 30 kg light. You should be able to adapt the details of this solution to the 33 kg traffic light in the current edition:
The net force on the light is 0. This means that the net force in the vertical direction will be 0 and likewise for the net force in the horizontal direction.
We'll let the x axis be horizontal and the y axis vertical and upward.
Let T1 be the tension in the 37 deg wire and T2 the tension in the 53 deg wire. Assuming that the 37 deg is with the negative x axis then T1 acts at the angle 180 deg - 37 deg = 143 deg.
Gravity exerts a downward force of 30kg * 9.8 m/s^2 = 294N.
The x and y components of the forces are as follows:
x y
weight 0 -294 N
T1 T1 cos(143 deg) T1 sin(143 deg)
T2 T2 cos(53 deg) T2 sin(53 deg)
The net force in the x direction is
T1 cos(143 deg) + T2 cos(53 deg) = -.8 T1 + .6 T2
The net force in the y direction is
T1 sin(143 deg) + T2 sin(53 deg) - 294 N = .6 T1 + .8 T2 - 294 N.
These net forces are all zero so
-.8 T1 + .6 T2 = 0 and
.6 T1 + .8 T2 - 294 N = 0.
Solving the first equation for T1 in terms of T2 we obtain T1 = .75 T2.
Plugging this result into the first equation we get
.6 ( .75 T2) + .8 T2 - 294 N = 0 which we rearrange to get
1.25 T2 = 294 N so that
T2 = 294 N / 1.25 = 235 N approx.
Thus T1 = .75 T2 = .75 * 235 N = 176 N approx.. **
Self-critique (if necessary):
Self-critique Rating:
Question: `qQuery problem 9.19 172 cm person supported by scales reading 31.6 kg (under feet) and 35.1 kg (under top of head).
Your solution:
Confidence rating::
Given Solution:
`a****The solution given here is for a person 170 cm tall, rather than 172 cm tall. You should be able to adapt the given solution to the 172 cm height; all distances will increase by factor 172 / 170 = 86 / 85, a little more than 1%:
The center of gravity is the position for which the net torque of the person is zero. If x represents the distance of this position from the person's head then this position is also 170 cm - x from the person's feet.
The 35.1 kg reading indicates a force of 35.1 kg * 9.8 m/s^2 = 344 N and the 31.6 kg reading indicates a force of 31.6 kg * 9.8 m/s^2 = 310 N, both results approximate.
About the point x cm from the head we then have the following, assuming head to the left and feet to the right:
}torque of force supporting head = -344 N * x
torque of force supporting feet = 310 N * (170 cm - x).
Net torque is zero so we have
-344 N * x + 310 N * (170 cm - x) = 0. We solve for x:
-344 N * x + 310 N * 170 cm - 310 N * x = 0
-654 N * x = -310 N * 170 cm
x = 310 N * 170 cm / (654 N) = 80.5 cm.
The center of mass is therefore 80.5 cm from the head, 89.5 cm from the feet. **
Principles of Physics and General College Physics Problem 9.2: 58 kg on diving board 3.0 m from point B and 4.0 m from point A; torque about point B:
The torque exerted by the weight of the 58 kg person is
torque = moment arm * force = 3.0 meters * (58 kg * 9.8 m/s^2)
= 3.0 meters * 570 N
= 1710 meter * newtons.
Self-critique (if necessary):
Self-critique Rating:
Question: `qPrinciples of Physics and General College Physics Problem 9.30: weight in hand 35 cm from elbow joint, 2.0 kg at CG 15 cm from joint, insertion 6.0 cm from joint. What weight can be held with 450 N muscle force?
Self-critique (if necessary):
Self-critique Rating:
Question: `qQuery gen problem 9.32 arm mass 3.3 kg, ctr of mass at elbow 24 cm from shoulder, deltoid force Fm at 15 deg 12 cm from shoulder, 15 kg in hand.
Give your solution:
Your solution:
Confidence rating::
Given Solution:
`a**The total torque about the shoulder joint is zero, since the shoulder is in equilibrium.
Also the net vertical force on the arm is zero, as is the net horizontal force on the arm.
The 3.3 kg mass of the arm experiences a downward force from gravity of w = 3.3 kg * 9.8 m/s^2 = 32 N, approx. At 24 cm from the joint the associated torque is 32 N * .24 m = 8 m N, approx.
THe 15 kg in the hand, which is 60 cm from the shoulder, results in a torque of 15 kg * 9.8 m/s^2 * .60 m = 90 m N, approx.
}The only other force comes from the deltoid, which exerts its force at 15 degrees from horizontal at a point 12 cm from the joint. If F is the force exerted by the deltoid then the resulting torque is F * sin(15 deg) * .12 m = .03 F, approx..
If we take the torques resulting from gravitational forces as negative and the opposing torque of the deltoid as positive then we have
- 8 m N - 90 m N + .03 F = 0 (sum of torques is zero),
which we easily solve to obtain F = 3300 N.
This 3300 N force has vertical and horizontal components 3300 N * sin(15 deg) = 800 N approx., and 3300 N * cos(15 deg) = 3200 N approx..
The net vertical force on the arm must be zero. There is a force of 800 N (vert. comp. of deltoid force) pulling up on the arm and 32 N (gravitational force) pulling down, which would result in a net upward vertical force of 768 Newtons, so there must be another force of 768 N pulling downward. This force is supplied by the reaction force in the shoulder as the head of the humerus is restrained by the 'socket' of the scapula and the capsule of ligaments surrounding it.
The net horizontal force must also be zero. The head of the humerus is jammed into the scapula by the 3200 N horizontal force, and in the absence of such things as osteoporosis the scapula and capsule easily enough counter this with an equal and opposite force. **
Self-critique (if necessary):
Self-critique Rating:
Question: `qUniv. 11.62 (11.56 10th edition). .036 kg ball beneath .024 kg ball; strings at angles 53.1 deg and 36.9 deg to horiz rod suspended by strings at ends, angled strings .6 m apart when joining rod, .2 m from respective ends of rod. Tension in strings A, B, C, D, E, F (lower ball, upper ball, 53 deg, 37 deg, 37 deg end of rod, 53 deg end).
Your solution:
Confidence rating::
Given Solution:
`a** Cord A supports the .0360 kg ball against the force of gravity. We have T - m g = 0 so
T = m g = .0360 kg * 9.8 m/s^2 = .355 N.
The second ball experiences the downward .355 N tension in string A, the downward force .0240 kg * 9.8 m/s^2 = .235 N exerted by gravity and the upward force Tb of tension in string B so since the system is in equilibrium
Tb - .355 n - .235 N = - and Tb = .59 N.
If Tc and Td are the tensions in strings C and D, since the point where strings B, C and D join are in equilibrium we have
Tcx + Tdx + Tbx = 0 and
Tcy + Tdy + Tby = 0.
Noting that strings C and D respectively make angles of 53.1 deg and 143.1 deg with the positive x axis we have
Tby = =.59 N and Tbx = 0.
Tcx = Tc cos(53.1 deg) = .6 Tc Tcy = Tc sin(53.1 deg) = .8 Tc
Tdx = Td cos(143.1 deg) = -.8 Td Tdy = Td sin(143.1 deg) = .6 Td.
So our equations of equilibrium become
.6 Tc - .8 Td = 0
.8 Tc + .6 Td - .59 N = 0.
The first equation tells us that Tc = 8/6 Td = 4/3 Td.
Substituting this into the second equation we have
.8 (4/3 Td) + .6 Td - .59 N = 0
1.067 Td + .6 Td = .59 N
1.667 Td = .59 N
Td = .36 N approx. so that
Tc = 4/3 Td = 4/3 (.36 N) = .48 N approx..
Now consider the torques about the left end of the rod. We have torques of
-(.200 m * Td sin(36.9 deg)) = -.200 m * .36 N * .6 = -.043 m N (note that this torque is clockwise, therefore negative).
-(.800 m * Tc sin(53.1 deg) = -.800 m * .48 N * .8 = -.31 m N and
1.0 m * Tf, where Tf is the tension in string F.
Total torque is 0 so
-.043 m N - .31 m N + 1.0 m * Tf = 0 and
Tf = .35 N approx..
The net force on the entire system is zero so we have
Te + Tf - .59 N = 0 or
Te = .59 N - Tf = .59 N - .35 N = .24 N. **
STUDENT QUESTION:
Why does the given solution find the torque of the system to
calculate the tension of E and F? Can't you just use the
same logic as you did to find Tension C and B to find it? In other words, Tex +
Tfx = 0 and Tey + Tfy = 0.588N.
Actually I see that this won't work because the weight is not in the center of
the system, but how would finding the torque
help us.
INSTRUCTOR RESPONSE:
Excellent questions.
The conditions of equilibrium are as follows:
-
each mass is in x and y equlibrium, as is any combination of masses, including the entire system
-
each object is in rotational equilibrium, i.e., the torque on each object is zero
We can use the conditions of x and y equilibrium to find the
tensions in all the strings except the ones supporting the ends of the rod., as
was done in the given solution.
We know the sum of the tensions in the strings supporting the rod (they add up
to .59 N, the sum of all the weights being supported).
However at this point we don't know how these tensions are balanced, as they
must be in order to prevent rotation. The conditions of x and y equilibrium have
taken us as far as they can. So we now need to consider rotational equilibrium.
-
We could have taken the torques about any point on the rod.
-
We chose to use an endpoint because the tension in the string at that point contributes nothing to the torque about this point, leaving us one less unknown in our equation.
Self-critique (if necessary):
Self-critique Rating: