Graph Trapezoids

You won't know what any of this means until you do it. Then, up to a point, it will all be obvious. The relational thing takes some real work with a lot of problems and exercises and, just like chess, the individual moves are simple but the game is complex. The difference is that this game is finite, whereas chess is at least practically infinite.

This isn't exactly typical. In your assignments you're going to have to build your own structure from experience and activity.

Our immediate goal is the understand how the word 'Relate' is used in listing course objectives, and even more importantly how this can help us think about what it means to understand a topic.

The basic idea of the word 'relate' is the following:

If we know a bunch of things, maybe we can put some of them together and figure out new things.

If we know a bunch of things, maybe we can pick just a few of them that could have been used to figure out all the others (if we didn't already know them).

... and maybe, if we do use a few things to figure out the others, we'll find that we were wrong about some of them.

That's pretty abstract, so let's look at a few specific examples:

First example:

Here's a small bunch of things:

{one number, another number, the sum of the two numbers}

Just to be really clear we might add the the 'sum' of two numbers is what we get when we add them. (This statement is actually sort of backward because the idea of 'sum' comes before the idea of addition, but we aren't going to worry about that right now)

There are only three things in this bunch.

If we know two of the things, then we can figure out the third. Specifically:

if we know the first number and the second, we can add them to get the third

if we know the first number and the sum of the two numbers, we can subtract the first number from the sum and get the second

if we know the second number and the sum of the two numbers, we can subtract the second number from the sum and get the first

We also understand that if we only know one of the three things, we can't find the other two.

So we know everything that can be known about how these three things are related.

This is what it means to 'Relate' a bunch of things.

Notice that I went ahead and listed the three things, separated by commas, between a set of braces { }. When I do that I can call the whole thing a set.

So here's a first attempt to define the word 'Relate':

We can 'Relate' a bunch of things if we know every way two or more things can be combined to get other things, and we know every combination that can be used to figure out the whole bunch.

Second example:

Here's another small bunch of things:

{one number, another number, the sum of the two numbers, the product of the two numbers}

There are four things in this bunch. (We can also say that there are four elements in this set.)

Can some of these things be related to others?

Obviously if we know the two numbers, we can add them to find their sum and multiply them to find their product.

So from the two numbers, we can find everything else in the bunch.

We say that the set

{one number, another number}

generates the set

{one number, another number, the sum of the two numbers, the product of the two numbers}

Also, if we know the first number and the sum, we can subtract to find the second number. Then knowing the two numbers we can multiply them to find their product.

So from one number and the sum of the two numbers, we can again find the whole bunch.

We say that the set

{one number, sum of the two numbers}

generates the set

{one number, another number, the sum of the two numbers, the product of the two numbers}

How many other ways can you find to combine two or more of these things to find the rest?

It turns out that we can prove that any two of these things can be used to find the other two.

But to do so we have to prove that if we know the product and the sum of two numbers, we can find the two numbers.

You can probably figure out what two numbers have a sum of 6 and a product of 8.

But can you figure out what two numbers have a sum of 23 and a product of 107?

That requires some algebra, and not everyone who has had algebra can do this.

An even fewer can prove that it's always possible, given the sum and product of two numbers, to find the numbers.

So what have we learned about the idea of 'Relate'?

It's easy to see that someone who knows only arithmetic can understand a lot about how to 'Relate' the set

{one number, another number, the sum of the two numbers, the product of the two numbers}.

However you have to know some stuff that goes beyond arithmetic, and be fairly clever as well (or be within a few days of a test on the topic), to prove that any two of these things are enough to figure out the the other two.

So

Some bunches of things can be partially related, some can be completely related, but not everyone can completely understand all the relationships.

That's the way it is with most knowledge.

In this course the better you understand the relationships, the better you are likely to do.

To help out

We list most of the sets to be related.

You master the relationships by practicing them, mostly by solving problems.

************************

We're going to continue our discussion with another example. In this case

our set has 10 elements (that is there are 10 things in the bunch we want to relate)
there are over 1000 subsets
you probably couldn't list them all even if you took the time

but, most importantly

you probably are able to 'Relate' the set

Furthermore

you won't need to do so, but you can probably prove that you can 'Relate' this set.

Here's the example:

Take a look at the graph below:

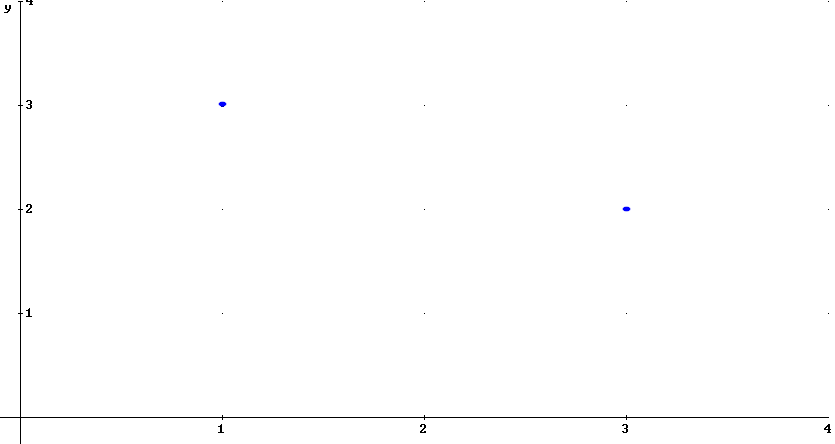
There are two points indicated by blue (and slightly elliptical) dots.

Can you answer the following questions?

What is the x coordinate of the first point, which we will take to be the point to the left?

If x_1 stands for the x coordinate of the first point, then what is the value of x_1?

If y_1 stands for the y coordinate of the first point, then what is the value of y_1?

If (x_1, y_1) is the ordered pair that represents the first point, then how do we write the ordered pair (x_1, y_1) with actual numbers in place of the symbols x_1 and y_1?

What do you think is the ordered pair (x_2, y_2)?

Where is the line segment that joins point 1 to point 2? Can you sketch the graph and sketch this line segment?

What is the 'rise' from the first point to the second?

You probably don't need the answers to these questions, but just in case:

The answer to question 2 is 1, since the x coordinate of the first point is 1 and x_1 said to stand for this coordinate.

The answer to question 5 is (3, 2). We haven't really said that (x_2, y_2) stands for the ordered pair representing the second point, but you probably made this connection based on what was stated in the first few questions.

The answer to question 4 is (1, 3), since the x coordinate of the first point is 1 and the y coordinate is 3.

The answer to question 7 is -1, since the 'rise' between two points is the change in the y value between these points. If we move from the first point to the second we move 2 units to the right and 1 unit downward, giving us a 'rise' of -1.

The answer to question 1 is 1, since the x coordinate of the first point is 1.

The answer to question 3 is 3, since the y coordinate of the first point is 3 and y_1 is said to stand for this coordinate.

... easier: For example if we know ... and ... and ... we can figure out all the rest. In a nutshell that's the key to understanding what 'relate' means. 'relate' means that we can always tell if our information is enough to determine everything, and if we wanted to take the time we could list all the combinations that would do the job

Objective, sets, bulleted list or set notation, evaluation, rubric

Now we're going to state an objective that might well be part of a precalculus, calculus or physics course. A lot of this will look like nonsense right now, but we're gradually going to make sense of all of it:

Objective:

Relate symbolically or numerically

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}

U

{point 1, graph of y vs. x coordinate plane, rise, run, slope, distance, midpoint, length}

U

{change in x, change in y, average rate of change of y with respect to x, difference quotient, slope of y vs. x graph}

U

{average y value, region beneath segment, graph trapezoid, graph altitudes, average graph altitude, trapezoid 'width', trapezoid area}

U

{interpretation for depth vs. clock time, interpretation for money vs. clock time, interpretation for pay rate vs. clock time, interpretation for temperature vs. clock time, interpretation in terms of pond width vs. position, interpretation for pond area vs. depth}

where

graphs are constructed in the x-y coordinate plane

y_1 and y_2 are both positive

'graph of points' defined as the y vs. x coordinate plane with the points (x_1, y_1) and (x_2, y_2) indicated and labeled

'segment' defined as straight line segment joining point_1 and point_2

... and before you know it you've learned (or reviewed) some mathematics

We've used the notation of sets to state this objective. There are other more common ways of stating objectives, and we will do so in many cases, but this way is more general and more powerful. It will also be more useful to some students.

You should already be familiar, through your general mathematics education, with the notations used here, but just to be sure we're all talking about the same thing:

braces { } denote sets
when a list of things appears between the braces, separated by commas, those things are called the elements of the set
U denotes the operation of set union
the union of two or more sets consists of all the elements that appear in at least one of the sets

The objective is therefore stated in terms of the union of five sets.

From the example we considered earlier, you probably have a good idea of what we're talking about with the first of the five sets, the one that starts { x_1, y_1, x_2, y_2,

How many elements do you see in that set?

Do you see anything in that set you don't pretty much recognize from the previous example?

The first set is easy to understand.

Most of the other five sets aren't that hard to understand either.

We're going to take them one at a time.

We observe the following:

Each of the five sets that makes up this objective is a topic unto itself.
Each topic also related to the other topics.

Now let's be sure we understand the first of the five sets.

The first set is

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}.

You might not recognize it yet, but if you have completed the prerequisites for your course you already know how to 'Relate' this set. So you really don't have much of anything new to learn, except an additional way to look at what it means to understand something.

Here's a short exercise to help explain the meaning of this set:

Start by sketching yourself a set of x-y axes and graph the points represented by the ordered pairs (2, 4) and (5, 9).

Then sketch the line segment between these points.

Got it? Ok, then:

The first point is (x_1, y_1) and the second point is (x_2, y_2). What do you think are the values of x_1, y_1, x_2 and y_2?

link to solution/explanation for a different set of points

Now that you've got an example to help, let's take another look at our objective.

Look again at the very first of the five sets:

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}

The question told you to sketch a set of x-y axes (more properly called an x-y coordinate plane), gave you the points (2, 4) and (5, 9), then asked for the values of x_1, x_2, y_1 and y_2.

Did the given information tell you the value of x_1? It didn't; you figured out the value of x_1 from the given information.

It might seem obvious to you that the question did give you the value of x_1.

However you were not told the value of x_1. You figured out (or could have figured out) what x_1 had to be, after you were told that the first point was (x_1, y_1). Similarly you figured out (or could have figured out) the values of y_1, x_2 and y_2.

You also figured out, from the given information, where to put the points and where to draw the segment.

What you were given, then, were the coordinates of a point (x_1, y_1), and those of a second point (x_2, y_2), along with the information that these points were to be graphed on an x-y plane. We can say that you were given the information in the subset

{ (x_1, y_1), (x_2, y_2) }

from which you were able to figure out the information in the entire set

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}.

Now think about another possible subset of information:

What if you had been given the subset

{ graph of point 1, graph of point 2}

This means that you are given an x-y plane with the two points.

From the graph of the points you could easily graph the line segment joining them.

And you could easily see (or at least reasonably estimate) the values of x_1, y_1, x_2, y_2, the ordered pairs (x_1, y_1) and (x_2, y_2) and the 'rise'.

So once again you could figure out the information in the entire set

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}.

Our first set

{ x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point1, graph of point 2, graph of segment}

lists 10 elements. They are

x_1
y_1
x_2
y_2
(x_1, y_1)
(x_2, y_2)
rise
graph of point 1
graph of point 2
graph of segment

We have seen 2 subsets of this set from which we can figure out everything else in the whole set.

Each of these subsets happens to consist of 2 elements. The first subset consisted of

(x_1, y_1)
(x_2, y_2)

The second consisted of

graph of point 1
graph of point 2

We could at this point ask ourselves the following question:

Is every possible 2-element subset sufficient to figure out everything else in our 10-element set?

Take a minute and ponder this question. What do you think?

OK, it's fairly clear that is isn't so.

For example the set {x_1, x_2} is a 3-element subset but it just isn't enough. We need more information.

If we also knew the values of y_1 and y_2, we would have all the information we need. So if we add y_1 and y_2 to the set, then we can figure out where to put the two points on our graph we'll have a 4-element set that generates our entire 10-element set.

So we conclude that while some 2-element subsets have enough information to figure out all 10 elements, there's at least one 2-element subset that doesn't.

We could also ask a question like

How many two-element subsets are there that generate the entire set?

This might or might not be a question we want to think about. As you have seen, you can understand this set quite well without knowing the answers to such questions. If the goal of the course is just to 'Relate' this set, then it isn't necessary to think about such a question.

This is turning into a lot of discussion about a situation that's much easier to understand than the discussion itself. And the discussion could go on for awhile.

In fact, there are 1022 non-empty subsets which are smaller than our 10-element set, and a lot of interesting questions we could ask, such as:

What is the largest number of elements that won't generate the entire set?

How many 3-element subsets are there that generate the entire set?

Of all the 3-element subsets that generate the entire set, how many of them don't contain a 2-element subset that does so?

All these questions, and many more like them, can be answered.

These sorts of questions are interesting and can be important, but we're not studying set theory right now.

We're just trying to understand how the word 'Relate' can be used to help us think about what it means to know stuff.

There are also questions that can't be answered, such as

What is the prettiest set that determines the entire set?

Of all the sets that determine the entire set, which is the easiest to understand?

Which set would the good guys prefer?

Why can't we answer these questions? Or can we?

Now if I want to test you on the set, there are a whole lot of questions I could ask. For example:

Question: Sketch a graph of the points (7, 4) and (12, 8) and the segment joining them. Then determine the 'rise' from the first point to the second.

Question: If you know the values of x_1, x_2, y_1 and y_2 is it possible to sketch a graph of the line segment joining the points (x_1, y_1) and (x_2, y_2)?

You understand this situation, and you can probably answer the above. You can probably answer just about any other question I could ask you about how the 10 elements of our set are related.

The following questions don't ask directly about how things in the set are related, but rather they ask you to apply what you know about the relationships. You could probably answer the following:

Question: If the point shown on the graph below is represented by the ordered pair (x_1, y_1), then what are the values of x_1 and y_1? What would be the values of x_2 and y_2 for the point which is 1 unit to the right and 2 units lower than this point?

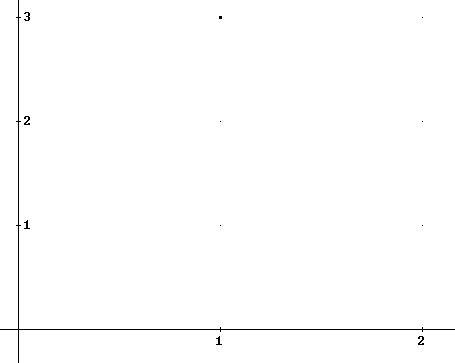
Question: If the point shown on the graph above is (x_1, y_1), what are the values of x_2 and y_2 for the point (x_2, y_2) that lies twice as close to the x axis and twice as far from the y axis?

These problems can be solved based on your understanding of the elements of the set { x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}.

At this point you understand what is meant by the objective

'Relate { x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment}, where

x_1, y_1, x_2, y_2 are numbers,

(x_1, y_1) is the ordered pair representing the point called 'point 1' on a y vs. x graph whose x coordinate is x_1 and whose y coordinate is y_1,

(x_2, y_2) is similarly defined, and

'segment' is the line segment joining point 1 and point 2.'

We could also express this in bulleted form as

Relate

x_1

y_1

x_2

y_2

(x_1, y_1)

(x_2, y_2)

rise

graph of point 1

graph of point 2

graph of segment

Symbolic

The set { x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), rise, graph of point 1, graph of point 2, graph of segment} is just the first of five sets that make up our Objective.

Before we consider the second of our sets, let's go back to our first picture. We understand that picture quite well at this point, so we're going to go ahead and build on our understanding with a few more questions.

Here's the picture again:

See if you can answer the following questions. In case you can't answers will follow.

What is the rise from the first point to the second?
What is the run from the first point to the second?
What is the slope from the first point to the second?
What is the midpoint of the line segment from the first point to the second?
How far is the first point from the second?
How far is the second point from the first?
What is the length of the segment between the two points?

Also consider the question

How many different quantities are related by these questions?

Answers:

The answer to question 3 is slope = rise / run = -1/2.
The answer to question 7 is that the segment is the hypotenuse of a right triangle with legs 1 and 2, so its length is sqrt(1^2 + 2^2) = sqrt(5).
The answer to question 2 is that the points are (1, 3) and (3, 2) so the run is from x = 1 to x = 3, a run of 3 - 1 = 2.
The answer to question 6 is that the distance between the points is the length of the line segment joining them. The segment is the hypotenuse of a right triangle with legs 1 and 2, so its length is sqrt(1^2 + 2^2) = sqrt(5), and this how far the second point is from the first.
The answer to question 1 is that the points are (1, 3) and (3, 2) so the rise is from y = 3 to y = 1, a rise of 1 - 3 = -2.
The answer to question 4 is that the segment goes from x = 1 to x = 3 so the midpoint is at x = 2, halfway between the x values; and from y = 3 to y = 2 so the midpoint is at y = 2.5, halfway between the y values. The midpoint is therefore the point (2, 2.5).
The answer to question 5 is that the distance between the points is the length of the line segment joining them. The segment is the hypotenuse of a right triangle with legs 1 and 2, so its length is sqrt(1^2 + 2^2) = sqrt(5), and this how far the first point is from the second.

What does this have to do with our objective?

The second of our sets is

{point 1, rise, run, slope, distance, midpoint, segment length}

Some observations about this set:

It should be clear that the last set of questions shows us a lot about how this set is related.

For example:

The set {rise, run} is sufficient to determine slope (remember that slope is equal to rise / run), distance and segment length (the last two equal to one another; either can be found using the Pythagorean Theorem). However from just this information we cannot determine point 1 or the midpoint of the segment, so the set {rise, run} does not generate the entire set.

The set {rise, run, point 1} is sufficient to determine everything.

The set {rise, run, midpoint} is sufficient to determine everything.

The above relationships can be figured out pretty easily by sketching a graph and applying general knowledge. This is true for most of the relationships that occur with this set.

However some of the relationships are at least moderately challenging.

For example:

The set {slope, distance, midpoint} is sufficient to generate the entire set, but requires algebra and significant problem-solving skills.

So, as before with the set {one number, another number, sum of the two numbers, product of the two numbers}, we have encountered a set where most of the relationships are fairly easy to understand, but some are significantly more difficult.

This second set {point 1, rise, run, slope, distance, midpoint, segment length} is also related to our first set. If we put the two sets together we get the intimidating-looking set

union of first two sets: { x_1, y_1, x_2, y_2, (x_1, y_1), (x_2, y_2), graph of y vs. x coordinate plane, graph of point 1, graph of point 2, graph of segment, rise, run, slope, distance, midpoint, length, point 1}

This set has 17 elements, and over a hundred thousand subsets. But from the examples and questions we've looked at, and from what you knew when you started, you can handle almost all of the relationships. You understand these quantities and their relationships pretty well. However some of the relationships are challenging. You have to be pretty well practiced as well as clever in order to understand and apply all the possible relationships.

When you do know all of the relationships, and know how to apply them to a variety of situations, you can be said to have 'mastered' the set.

Most students who have done well in prerequisite courses have the ability, given a reasonable amount of time and focused effort, to become functional with the relationships we encounter in this course.

Actual mastery is more difficult. Most students lack the combination of time, focus and ability necessary to fully master all the topics. Hence partial credit ... and other excuses

... where rise and run are... distance is ... etc.

Next we move to less familiar territory, where you must be alert to the constant danger of learning something. This requires a lot of presence of mind, careful focus and ...

{change in x, change in y, average rate of change of y with respect to x, difference quotient, slope of y vs. x graph}