Quiz 0210
Find the average rates of change of the function y(t) = 7 * 2^-t on each of the following intervals:
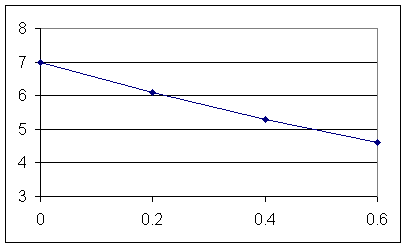
The y values at t = 0, .2, .4, .6 are 7, 6.094, 5.305, 4.618.
The changes in the y values are `dy , taking values -.906, -.789, -.683.
Changes in t are .2.
The average rates of change are `dy / `dt taking values -4.53, -3.94, -3.43 (e.g., the first rate is `dy / `dt = -.906 / .2 = -4.53.).
The graph below indicates the t = 0, .2, .4, .6 points of the graph. Note that the average rate between two consecutive points is
ave rate = change in y / change in t = `dy / `dt = rise / run = slope
That is the average rate on an interval is represented by the slope of the graph on that interval.

The table shown below indicates the values if t, the values of y(t) and for each interval the values of `dt, `dy and average rate = `dy / `dt:
| t | y(t) = 7 * 2^-t | `dt | `dy | ave rate = `dy / `dt |
| 0 | 7 | |||
| 0.2 | 6.093853943 | 0.2 | -0.906146057 | -4.530730285 |
| 0.4 | 5.305007983 | 0.2 | -0.78884596 | -3.944229801 |
| 0.6 | 4.618277688 | 0.2 | -0.686730295 | -3.433651475 |
On the first three intervals you calculated above, do the rates of change change by the same amount as you go from one interval to the next?
Between the first and second interval the rate of change goes from -4.53 to -3.94, which is a difference of +.59.
Between the second and third interval the rate of change goes from -3.94 to -3.43, which is a difference of +.51.
These changes in rate are not the same.
As we've seen in previous classes, the rate of change changes by a constant amount of equal intervals if and only if the function is quadratic. This function is exponential, not quadratic.
For the same function find the expression for the average rate of change on the interval from t to t + `dt.
Average rate of change = change in y / change in t = ( y(t+`dt) - y(t) ) / `dt.
Since y(t) = 7 * 2^-t so
and the average rate becomes
change in y / change in t =
( y(t+`dt) - y(t) ) / `dt =
( 7 * 2^-(t+`dt) - 7 * 2^-t) / `dt
If y(t) represents the temperature of an object at clock time t, then what do the slopes of the graph represent?
The slope is rise / run.
What do rise and run represent?
So what does slope represent?
change in temperature / change in clock time =
average rate of change of temperature with respect to clock time.
What is an expression for the slope between the points (1, 3) and (7, 5)?
slope = rise / run. Rise is change in y coordinate, run is change in x coordinate. So rise = 5 - 3 = 2 and run = 7 - 1 = 6. Thus
slope = rise / run = 2 / 6 = 1/3.
What is an expression for the slope between the points (1, 3) and (x, y)?
The rise from (1, 3) to (x, y) is y - 3.
The run from (1, 3) to (x, y) is x - 1.
So the slope is
slope = rise / run = (y-3) / (x-1).
What equation expresses the claim that the slope between the points (1, 3) and (7, 5) is equal to the slope between the points (1, 3) and (x, y)?
The slope between (1, 3) and (7, 5) is
(5-3) / (7-1).
The slope between (1, 3) and (x, y) is (y-3) / (x-1).
The two are equal if
(5-3) / (7-1)= (y-3) / (x-1).
We note that the two slopes are equal if and only if (x,y) lies on the line defined by the two points (1, 3) and (5, 7).
What do you get when you solve this equation for y?
To solve (5-3) / (7-1)= (y-3) / (x-1) for y:
multiply both sides by (x-1) and then add 3 to both sides to get
y = 1/3 (x-1) + 3.
Expand and simplify to get
y = 1/3 x + 8/3.
This equation holds if and only if (x,y) lies on the line defined by the two points (1, 3) and (5, 7).
This is therefore called the equation of the straight line through the two given points.