Quiz 0224
If y = f(x) = x then quickly sketch graphs of the following:
∑ y = .2 f(x)
The basic points (0, 0) and (1, 1) are vertically stretched to give us (0, 0) and (1, .2). The resulting graph is the straight line thru these points.
∑ y = f(x) - 3
The basic points are vertically shifted -3 units, moving the basic points to (0, -3) and (1, -2). The resulting graph is the straight line thru these points.
∑ The family y = f(x) + c for c values from -3 to +2.
The graph of y = f(x) + c is vertically shifted c units from the graph of y = f(x), so the lowest graph will lie 3 units below the y = x graph and the highest will lie 2 units above the y = x graph. All vertically shifted graphs in between the lowest and the highest will be included.
The DERIVE command that gives us the graphs for c = -3, -2, -1, 0, 1 and 2 is
VECTOR(y = x + c, c, -3, 2, 1)
and the resulting graph is shown below.
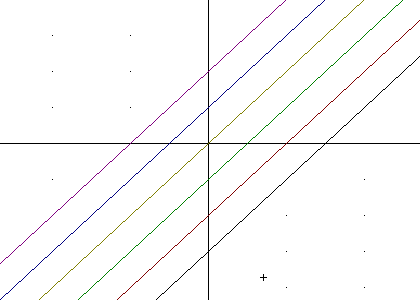
The DERIVE command that gives us the graphs for c = -3, -2.9, -2.8, ... , 1.9, 2 is
VECTOR(y = x + c, c, -3, 2, ,1)
and the resulting graph is shown below.
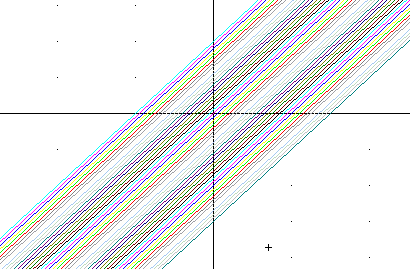
∑ The family y = A f(x) for A values -.5 to +2.
If we multiply f(x) by A then every y value will become A times as great, which vertically stretches the graph by factor A. The graphs in this family will vertically stretch the basic points (0, 0) and (1, 1) by factors as low as -.5 and as high as 2. The stretch by factor -.5 will change the basic points to (0, 0) and (1, -.5), resulting in a graph with slope -.5. The stretch by factor 2 will change the basic points to (0, 0) and (1, 2), resulting in a graph with slope 2. Every slope between -.5 and 2 will occur, and every graph will pass through (0, 0).
The DERIVE command VECTOR(a∑x, a, -0.5, 2, 0.1) gives us the graph shown below:

If y = f(x) = 3x - 4 then
∑ What are the coordinates of the x = 2 and x = 5 points of the graph?
When x = 2 we get y = f(2) = 2
When x = 2 we get y = f(5) = 11.
Our two graph points are therefore (2, 2) and (5, 11).
∑ What is the slope of the line segment between these two points?
Rise = 11 - 2 = 9
Run = 5 - 2 = 3
Slope = rise / run = 9 / 3 = 3.
If y = f(x) = 3x - 4 then
∑ What is the symbolic expression for the coordinates of the graph point for which x = x1?
y1 = 3 * x1 - 4 so the coordinates are (x1, 3 * x1 - 4)
∑ What is the symbolic expression for the coordinates of the graph point for which x = x2?
y2 = 3 * x2 - 4 so the coordinates are (x2, 3 * x2 - 4)
∑ What is the symbolic expression for the rise between these points?
The rise is the change in the y coordinate, which in this case would be ( 3 * x2 - 4 ) - ( 3 * x1 - 4).
∑ What is the symbolic expression for the run between these points?
The run is the change in the x coordinate, which is x2 - x1.
∑ What is the symbolic expression for the slope between these points?
slope = rise / run = [ ( 3 * x2 - 4 ) - ( 3 * x1 - 4) ] / (x2 - x1), which simplifies to ( 3 * x2 - 3 * x1) / (x2 - x1) by just simplifying the numerator, then to 3(x2-x1) / ((x2 - x1) by factoring the 3 out of the numerator, and finally to just 3 since (x2-x1) / (x2-x1) = 1.
In terms of a graph of f(x) vs. x,
∑ What does the expression ( f(x2) - f(x1) ) represent?
This expression represents the rise from the point (x1, f(x1) ) to the point (x2, f(x2) ).
∑ What does the expression x2 - x1 represent?
This expression represents the run from the point (x1, f(x1) ) to the point (x2, f(x2) ).
∑ What does the expression ( f(x2) - f(x1) ) / (x2 - x1) represent?
This expression represents rise / run from the point (x1, f(x1) ) to the point (x2, f(x2) ).
If f(x) = 1.3 x + 2 then
∑ What is the x-intercept of the graph of f(x) vs. x?
∑ What is the y-intercept of the graph of f(x) vs. x?
∑ How do we get from the x=0 point to the x=1 point of this graph?
∑ Sketch the graph based on only the information you gave in the three preceding questions.
If demand(price) = 200 - 3 * price, where price is in dollars, then
∑ How many units will be demanded if price = 30?
If price = 30 then demand(price) = demand(30) = 200 - 3 * 30 = 110.
∑ By how much does demand change for every additional dollar of price? Does the answer depend on the iniitial price?
The demand goes down by 3 units for every unit of increase in price.
∑ At what price will demand be zero?
∑ What is the demand if the commodity is given away free?
∑ Assuming that every object demanded is sold at the corresponding price, what function describes the number of dollars of revenue as a function of price?
∑ Describe the graph of revenue vs. price.
For the revenue vs. price function of the preceding example,
∑ What is the rise of the graph between the points where price = 30 and price = 40 and what does the rise mean?
∑ What is the run of the graph between the points where price = 30 and price = 40 and what does the run mean?
∑ What is the average slope of the graph between the points where price = 30 and price = 40 and what does the slope mean?
∑ What is the equation of the straight line through the points where price = 30 and price = 40?
If the length of a spring is 30 cm when no weight is suspended and the length increases by 5 cm for every additional pound of suspended weight then
∑ What function length(weight) describes the length of the spring in terms of the weight?
∑ What is the meaning of the slope of this graph?
∑ What is the meaning of the y intercept of this graph?
For the number sequence 11, 14, 17, 20, 23, ...
∑ What is the pattern of the sequence?
∑ What function f(n) can be used to give the numbers in the sequence?
If a(n) = a(n-1) + 5, with a(0) = 12, then what are the terms a(1), a(2), a(3) and a(4)?
Common Errors on Major Quiz:
1. Incorrect shifting and stretching.
-
Shifts move every point by the same amount.
-
Vertical stretches move points at different distances from the x axis through different displacements.
-
If a function has a horizontal asymptote to the x axis a vertical stretch will not change the location of that asymptote. A vertical shift will change the location of a horizontal asymptote.
-
Know the basic points of the function and specify exactly where each one goes at each step of the transformation.
2. Getting only one coordinate of the vertex.
-
To get the vertex of a parabola you have to get the x coordinate using x = -b / (2a), and you also have to plug this x coordinate into the function to get the y coordinate of the vertex.
3. Getting a negative under the square root and not saying that this gives you no real solution:
-
If you get a negative under the square root this means that there is no real solution and you have to say so, and you have to say what this tells you about the situation.
4. Getting the vertex of a parabola but not the points one unit right and left.
-
The vertex is the axis of symmetry of the parabola. The coefficient of t^2 is the vertical stretch factor, so the points one unit right and left of the axis of symmetry are vertically displaced a units in the vertical direction.
5. y = x^-p has vertical asymptote(s)
-
If p is a positive number then x^-p = 1 / x^p, and as x -> 0 this quotient approaches infinite magnitude. This gives you vertical asymptote(s) at x = 0. There isnít a point on the y axis, and the function never levels off to go through such a point.
6. Explain why the slope represents what it does.
-
Explain what the rise means, explain what the run means, both in the context of the problem, and explain in that context what it means to divide the rise by the run.
interpretation of `dy / `dt
difference equation, sequence behavior
rate behavior