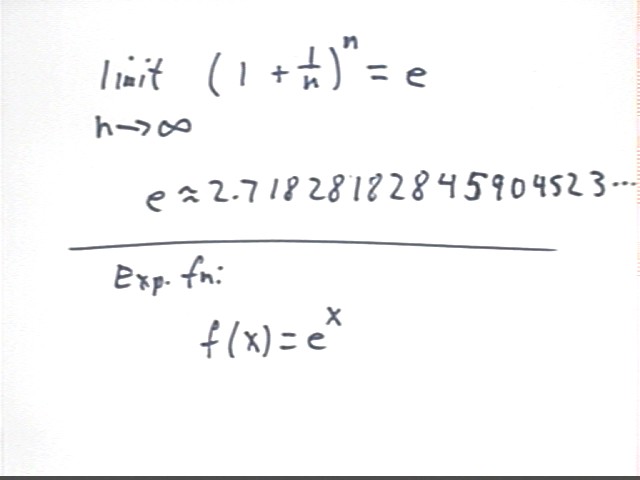Quiz 0325
1. What two equations do you get if you plug the data points (2,1) and (6,5) into the form y = A b^x?
The equations are 1 = A * b^2 and 5 = A * b^6.
2. Some moron ties his standard pickup truck to a tree and tries to stretch it by running all four wheels, which of course wouldn't stretch anything between the wheels. If the fool just used his front wheels, and if the truck was flimsy enough, it might in fact stretch out.
If the truck stretched out to 1.2 times its original length, what would happen to its weight?
Nothing. Things don't get heavier just because they're stretched.
If the truck was rescaled to 1.2 times the original length, without also scaling its height and width, it would get 1.2 times as heavy.
If we built a geometrically similar truck with all parts scaled up to 1.2 times their original linear dimensions, how many times more would it weigh?
Now if we actually build a scaled-up truck, instead of stretching an existing truck, all the little truck cubes will also scale up, which will give them 1.2^3 times the volume. So the weight would be 1.2^3 = 1.728 times as much.
For this sort of scaling we have y = k x^3, where y is weight and x is any linear dimension, say length. We can write this as
weight = k * length^3.
With this proportionality
weight2 / weight1 = (k * length2^3 / (k * length1^3) ) so
weight2 / weight1 = length2^3 / length1^3 or
weight2 / weight1 = (length2 / length1)^3.
So if length2 is 1.2 * length1 we get weight2 / weight1 = 1.2^3 = 1.728, as before.
For the preceding situation, how many times more paint would be required to cover the truck, assuming paint thickness is the same in all cases?
Paint covers the surface, which is covered by little squares. If we scale the linear dimension up by factor 1.2 all the little squares will grow to 1.2^2 times their original area.
The proportionality area = k * length^2 for surface areas can also be used to give us
area2 / area1 = k * length2^2 / ( k * length1^2), which simplifies to
area2 / area1 = (length2 / length1)^2.
So if area2 is 1.2 * area1 we get weight2 / weight1 = 1.2^2.
3. Same guy, apparently with more money than brains, loans $20,000 to the guy who owns the tree. The guy is going to pay back 4% interest on the original principle per year for the next 10 years, and at the end will give back the entire $20,000. The first guy could have invested the $20,000 at 4% annual interest, compounded annually.
How much will the first guy have at the end of 10 years, assuming he buries each year's interest in a secure box under the tree?
He's going to get 4% of $20,000 each year, or $800 per year. This goes on for 10 years so he ends up with $8000, plus his original $20,000, for a total of $28,000.
How much would he have had if he had invested the money to be compounded?
Compounding once a year he will end up with $20,000 ( 1.04)^10 = 29,604.
How much would he have if he managed to find someone to compound the interest continuously instead of annually?
Continuous compounding at annual rate r for t years multiplies your principle by e^(r t). So compounding continuously he will end up with
$20,000 * e^(.04 * 10) = 29,836.
How much would have have if at the end of each year he invested the annual interest the second guy is paying him at 4%, compounded annually?
The first $800 payment is at the end of the first year. It still has 9 years to grow. At 4% annual interest compounded annually it will grow to $800 ( 1 + .04 ) ^ 9.
The next $800 payment is invested for 8 years and will grow to $800 (1 + .04) ^ 8.
The remaining payments will grow to
$800 ( 1 + .04 ) ^ 7
$800 ( 1 + .04 ) ^ 6
$800 ( 1 + .04 ) ^ 5
$800 ( 1 + .04 ) ^ 4
$800 ( 1 + .04 ) ^ 3
$800 ( 1 + .04 ) ^ 2
$800 ( 1 + .04 ) ^ 1
$800 ( 1 + .04 ) ^ 0
So at the end of 10 years the interest payments will be worth
$800 [ 1.04^9 + 1.04^8 + 1.04^7 + 1.04^6 + ... + 1.04^0 ] = $800 ( 12.006) = $9604.80.
4. Solve the two equations you got for the first question.
We can solve these equations using a variety of different strategies.
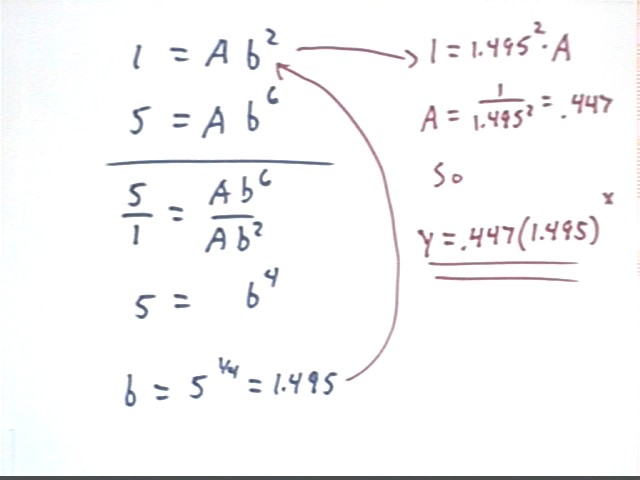
In the figure below we begin by solving the first equation for A, multiplying both sides by b^-2. We obtain
A = b^-2.
We could plug b^-2 in for A in the second equation, obtaining
5 = b^-2*b^6 or 5 = b^4,
which we could easily solve for b.
However that's not what we do below. Instead we solve the second equation for A:
Solving the second equation for A we multiply both sides by b^-6, obtaining A = 5 b^-6.
We then observe that we have two expressions for A, A = b^-2 and A = 5 b^-6.
These two expressions for A must be equal. So we obtain the equation
b^-2 = 5 b^-6.
We easily solve this for b, first multiplying both sides by b^6 to get
b^4 = 5
then finding the 1/4 power of both sides to get
b = 5^(1/4).
We would plug b = 5^(1/4) = 1.495 approx. into either of the original equations and solve that equation for A.

Another alternative solution to the system
1 = A b^2
5 = A b^6
is obtained by dividing one equation by the other, which will eliminate A.
Dividing the second equation by the first we end up with
5/1 = (A b^6) / (A b^2)
which we simplify to get
5 = b^4.
This gets us to the same point we reached in the previous solutions. We again find that b = 5^(1/4) = 1.495 approx.
Plugging this back into the first equation (follow the red arrows) we obtain
1 = A * 1.495^2,
which we easily solve to obtain A = .447.
It follows that our exponential function y = A b^x is
exponential function containing points (2,1) and (6,5) is
y = .447 * 1.495^x,
which is accurate to 3 significant figures.
If we start with principle P0 and compound interest at an annual rate of 100%, compounding once annually, how much do we end up with at the end of a year?
If we start with principle P0 and compound interest at an annual rate of 100%, compounding once annually, how much do we end up with at the end of a year?
What if we compound twice annually?
As shown in the figure below:
If we compound 100% annually, starting with P0, we end up at the end of the year with
(1 + 1.00) * P0 = 2 P0.
If we compound 100% twice annually, starting with P0, we apply 1/2 the 100% twice and end up at the end of the year with
(1 + 1.00/2)^2 * P0 = 2.25 P0.

Answer the same questions assuming that we compound 4 times annually (i.e., quarterly), monthly, weekly and daily? What if we compound 1000 times a year? What if we compound n times per year?
If we compound 100% four times annually, starting with P0, we apply 1/4 the 100% four times and end up at the end of the year with
(1 + 1.00/4)^4 * P0 = 2.44 P0.
If we compound 100% monthly, which is twelve times annually, starting with P0, we apply 1/12 the 100% twelve times and end up at the end of the year with
(1 + 1.00/12)^12 * P0 = 2.61 P0.
If we compound 100% weekly, which is 52 times annually, starting with P0, we apply 1/52 the 100% a total of 52 times and end up at the end of the year with
(1 + 1.00/52)^52 * P0 = 2.693 P0.
If we compound 100% daily, which is 365 times annually, starting with P0, we apply 1/365 the 100% a total of 365 times and end up at the end of the year with
(1 + 1.00/365)^365 * P0 = 2.71456 P0.
We see that the amount continues growing, but with each additional year the amount increases by less than in the preceding year.
If we compound 1000 times we end up with (1+1.00/1000)^1000 = 2.716923 P0 approx.
If we compound n times we end up with
end-of-year amount for n compoundings: (1+1.00/n)^n * P0.
Note that we report as many significant figures as we need to at least see the change from one number to the next. For n = 997 to n = 1004 the results (1 + 1/n)^n are shown below, and are seen to change in the 6th decimal place:
| number n of compoundings | (1 + 1/n)^n |
| 997 | 2.71691985 |
| 998 | 2.716921213 |
| 999 | 2.716922574 |
| 1000 | 2.716923932 |
| 1001 | 2.716925288 |
| 1002 | 2.71692664 |
| 1003 | 2.71692799 |
| 1004 | 2.716929337 |
Let f(n) = (1 + 1/n)^n. We've seen that
f(1) = 2
f(2) = 2.25
f(4) = 2.44
f(12) = 2.61
f(52) = 2.693
f(1000) = 2.716923
Using calculators we get
f(10,000) = 2.718145927
f(100,000) = 2.718268237
f(1,000,000) = 2.718281303 (note that many calculators will not give this result, due to the limitations of their arithmetic).
These numbers to approach a limit, which to 20 significant figures is
limit of (1+1/n)^n as n -> infinity is approximately 2.7182818284590452353.
This limit is an irrational number, never repeating, never establishing a pattern. We call the number e.
To 20 significant figures e = 2.7182818284590452353.
You should know that e = 2.718 approx.
Your calculator has an e^x button. If you calculate e^1 you will get the same result, up to the limit of your calculator's arithmetic.
The function y = e^x is the most basic of the exponential functions. We have also used y = 2^x as a basic exponential function. Your worksheets detail the relationship between these two functions.
Basically y = 2^x is the same as y = e^(kx) with k = ln(2). You will understand what this means in about a week.