040205

If g(t) = t^2 then give the t values for which g would be applied to arguments -1, 0 and 1, the y values taken at each argument, and the corresponding points on a graph of y vs. t:

• y = g(t-3)

The 'argument' of this function is t - 3. 

If g is applied to argument -1, then t - 3 = -1 so that t = 2.  The corresponding graph point is (2, 1).

If g is applied to argument 0, then t - 3 = 0 so that t = 3.  The corresponding graph point is (3, 0).

If g is applied to argument 1, then t - 3 = 1 so that t = 4.  The corresponding graph point is (4, 1).

In terms of a table, we see that the value of t is 3 greater than the value of the argument, which is why g(t-3) is shifted +3 units in the t direction:

 

t	argument t-3	g(t-3)
2	-1	1
3	0	0
4	1	1

• y = g(t+5)

Similarly the argument is t + 5 so the value of t is 5 less than that of the argument.  So the graph of g(t+5) will be shifted -5 units from the graph of g(t).

 

t	argument t+5	g(t+5)
-6	-1	1
-5	0	0
-4	1	1

The 'argument' of this function is t + 5. 

If g is applied to argument -1, then t + 5 = -1 so that t = -6.  The corresponding graph point is (-6, 1).

If g is applied to argument 0, then t + 5 = 0 so that t = -5.  The corresponding graph point is (-5, 0).

If g is applied to argument 1, then t + 5 = 1 so that t = -4.  The corresponding graph point is (-4, 1).

• y = g(t -12)

The 'argument' of this function is t - 12. 

If g is applied to argument -1, then t - 12 = -1 so that t = 11.  The corresponding graph point is (11, 1).

If g is applied to argument 0, then t - 12 = 0 so that t = 12.  The corresponding graph point is (12, 0).

If g is applied to argument 1, then t - 12 = 1 so that t = 13.  The corresponding graph point is (13, 1).

If g(t) = t^2 then give the vertical stretch, the horizontal shift and the vertical shift required to obtain each of the following from the graph of y = t^2.  Also give the points to which would the three points (-1, 1), (0, 0) and (1, 1) on the y = t^2 graph be transformed at each stage by each of the functions?

• 5 t^2

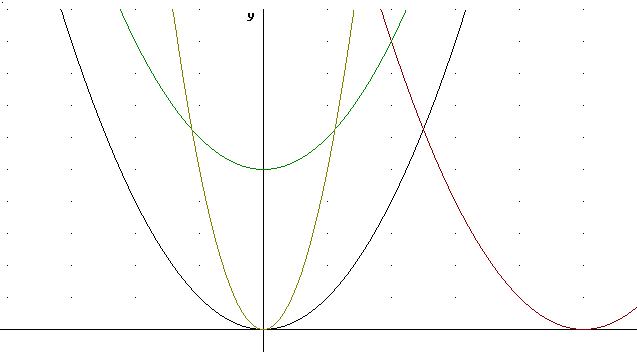
The y values of 5 t^2 are 5 times as great as the y values of g(t) = t^2, so the graph of 5 t^2 is vertically stretched by factor 5.

So y = 5 t^2 can be represented by the function 5 * g(t).

The basic points (-1, 1), (0, 0) and (1, 1) are transformed to (-1, 5), (0, 0) and (1,5).

• t^2 + 5

t^2 + 5 is g(t) + 5.

This function lies 5 units higher than that of g(t) = t^2.

This represents a vertical shift by factor 5.

The basic points (-1, 1), (0, 0) and (1, 1) are transformed to (-1, 6), (0, 5) and (1,6).

• (t – 5)^2

This is g(t-5).

The argument is 5 less than t so t is 5 greater than the argument.  This shifts everything +5 units in the t direction.

The basic points (-1, 1), (0, 0) and (1, 1) are transformed to (4, 1), (5, 0), (6, 1).

• (t + 5)^2

This is g(t+5).

The argument is 5 greater than t so t is 5 less than the argument.  This shifts everything -5 units in the t direction.

The basic points (-1, 1), (0, 0) and (1, 1) are transformed to (-6, 1), (-5, 0), (-4, 1).

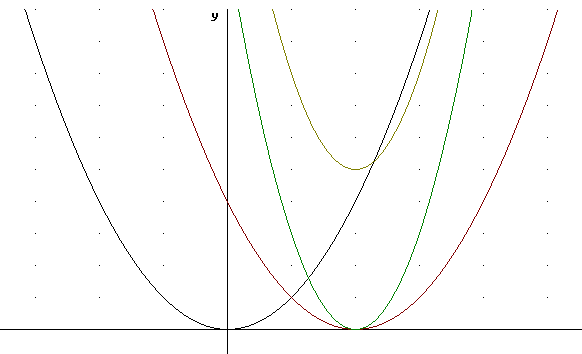
The figure below depicts g(t), g(t)+5, 5 g(t) and g(t-5).

• 5 t^2 + 3

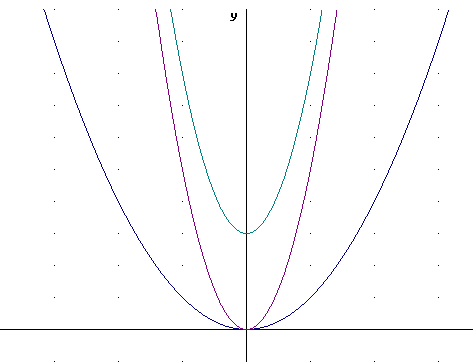
This can be expressed as 5 g(t) + 3.

The first thing that happens is the vertical stretch by factor 5. 

The basic points (-1, 1), (0, 0) and (1, 1) are transformed by the vertical stretch to (-1, 5), (0, 0) and (1, 5).

Then we vertically shift 3 units, which transforms the basic points we got from the preceding step to (-1, 8), (0, 3) and (1, 8).

The figure below depicts the graphs of g(t), 5 g(t) and 5 g(t) + 3.

• 2 (t-5)^2

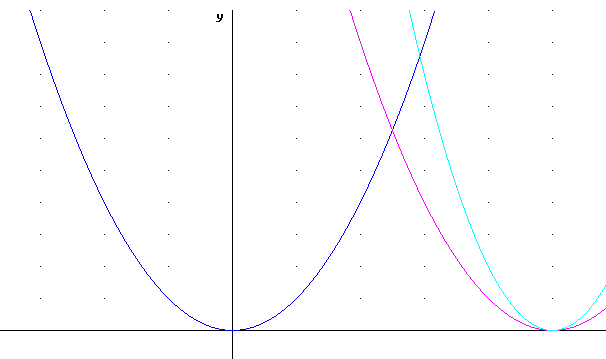
First apply the -5, which shifts every point 5 units to the right.

The basic points (-1, 1), (0, 0) and (1, 1) are transformed by this horizontal shift to (4, 1), (5, 0) and (6, 1).  The function at this point is g(t-5).

Then apply the 2, which vertically stretches the graph so that the preceding basic points become (4, 2), (5, 0) and (6, 2). 

The function we end up with is 2 g(t-5).

The figure below depicts g(t), g(t-5) and 2 g(t-5).

• 3 (t-2)^2 + 5

This function shifts 2 units in the t direction, then stretches by factor 3 then shifts +5 units in the vertical direction.

The function is 3 g(t) + 5.

Basic points go from (-1, 1), (0, 0), (1, 1) to (1, 1), (2, 0), (3, 1) to (1, 3), (2, 0), (3, 3) and finally to (1, 8), (2, 5), (3, 8).

The graphs of the original, intermediate and final functions are shown below:

If h(t) = 2^t  then give the t = -1, t = 0 and t = 1 points of the following, and graph the points:

• h(t)

The points are just (-1, 1/2), (0, 1) and (1, 2).

• 2 h(t)

The three points (-1, 1/2), (0, 1) and (1, 2) of the h(t) function are vertically stretched by factor 2 to give us (-1, 1), (0, 2) and (1, 4).

• .1 h(t)

The three points (-1, 1/2), (0, 1) and (1, 2) of the h(t) function are vertically stretched by factor .1 to give us (-1, .05), (0, .1) and (1, .2).

• h(t) + 4

The three points (-1, 1/2), (0, 1) and (1, 2) of the h(t) function are vertically shifted +4 units to give us (-1, 4.5), (0, 5) and (1, 6).

• 2 h(t) + 4

The three points (-1, 1/2), (0, 1) and (1, 2) of the h(t) function are first vertically stretched by factor 2 to give us (-1, 1), (0, 2) and (1, 4).

Then the points are vertically shifted +4 units to give us (-1, 5), (0, 6) and (1, 8).

• .1 h(t) + 4

The three points (-1, 1/2), (0, 1) and (1, 2) of the h(t) function are first vertically stretched by factor .1 to give us (-1, .05), (0, .1) and (1, .2).

Then the points are vertically shifted +4 units to give us (-1, 4.05), (0, 4.1) and (1, 4.2).

What are the functions that go with each of the preceding transformations?

• h(t) = 2^t, as given.
• 2 h(t) = 2 * 2^t
• .1 h(t) = .1 * 2^t
• h(t) + 4 = 2^t + 4
• 2 h(t) + 4 = 2 * 2^t + 4
• .1 h(t) + 4 = .1 * 2^t + 4.

If h(t) = 2^t then give the t values for which g would be applied to arguments -1, 0 and 1, the y values taken at each argument, and the corresponding points on a graph of y vs. t:

The 'argument' of this function is t - 3. 

If h is applied to argument -1, then t - 3 = -1 so that t = 2.  The corresponding graph point is (2, 1/2).

If h is applied to argument 0, then t - 3 = 0 so that t = 3.  The corresponding graph point is (3, 1).

If h is applied to argument 1, then t - 3 = 1 so that t = 4.  The corresponding graph point is (4, 2).

In terms of a table, we see that the value of t is 3 greater than the value of the argument, which is why h(t-3) is shifted +3 units in the t direction:

 

t	argument t-3	h(t-3)
2	-1	1/2
3	0	1
4	1	2

• y = h(t+5)

Similarly the argument is t + 5 so the value of t is 5 less than that of the argument.  So the graph of h(t+5) will be shifted -5 units from the graph of h(t).

 

t	argument t+5	h(t+5)
-6	-1	1/2
-5	0	1
-4	1	2

The 'argument' of this function is t + 5. 

If g is applied to argument -1, then t + 5 = -1 so that t = -6.  The corresponding graph point is (-6, 1/2).

If g is applied to argument 0, then t + 5 = 0 so that t = -5.  The corresponding graph point is (-5, 1).

If g is applied to argument 1, then t + 5 = 1 so that t = -4.  The corresponding graph point is (-4, 2).

• y = h(t -12)

The 'argument' of this function is t - 12. 

If h is applied to argument -1, then t - 12 = -1 so that t = 11.  The corresponding graph point is (11, 1/2).

If h is applied to argument 0, then t - 12 = 0 so that t = 12.  The corresponding graph point is (12, 1).

If h is applied to argument 1, then t - 12 = 1 so that t = 13.  The corresponding graph point is (13, 2).

If h(t) = 2^t then give the vertical stretch, the horizontal shift and the vertical shift required to obtain each of the following from the graph of y = 2^t.  Show also the sequence of transformations of the t = -1, 0, 1 points of the original h(t) vs. t graph:  

• 5 *2^t

The y values of 5 *2^t are 5 times as great as the y values of h(t) = 2^t, so the graph of 5 * 2^t is vertically stretched by factor 5.

So y = 5 * 2^t can be represented by the function 5 * h(t).

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed to (-1, 2.5), (0, 5) and (1,10).

• 2^t + 5

2^t + 5 is h(t) + 5.

This function lies 5 units higher than that of h(t) = 2^t.

This represents a vertical shift by factor 5.

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed to (-1, 5.5), (0, 6) and (1,7).

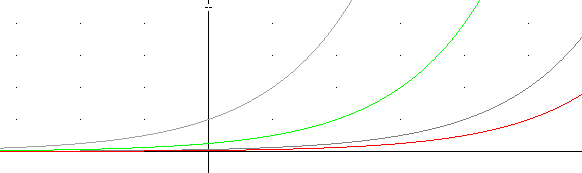
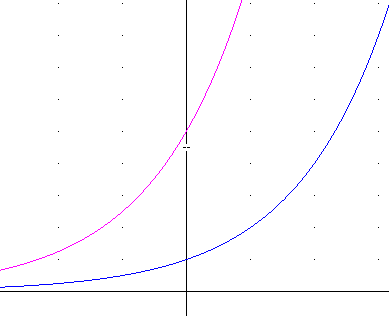
The figure below depicts the graphs of h(t) and 5 h(t)

• 2^(t – 5)

This is h(t-5).

The argument is 5 less than t so t is 5 greater than the argument.  This shifts everything +5 units in the t direction.

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed to (4, 1/2), (5, 1), (6, 2).

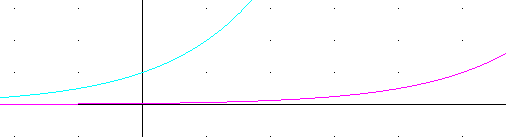
The figure below depicts h(t) and h(t-5).

• 2^(t + 5)

This is h(t+5).

The argument is 5 greater than t so t is 5 less than the argument.  This shifts everything -5 units in the t direction.

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed to (-6, 1/2), (-5, 1), (-4, 2).

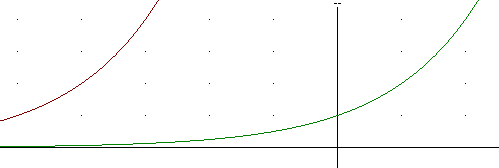
The figure below depicts h(t) and h(t+5).

• 5 * 2^t + 3

This can be expressed as 5 h(t) + 3.

The first thing that happens is the vertical stretch by factor 5. 

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed by the vertical stretch to (-1, 5), (0, 0) and (1, 5).

Then we vertically shift 3 units, which transforms the basic points we got from the preceding step to (-1, 8), (0, 3) and (1, 8).

The figure below depicts the graphs of h(t), 5 h(t) and 5 h(t) + 3.

• 2 * 2^(t-5)

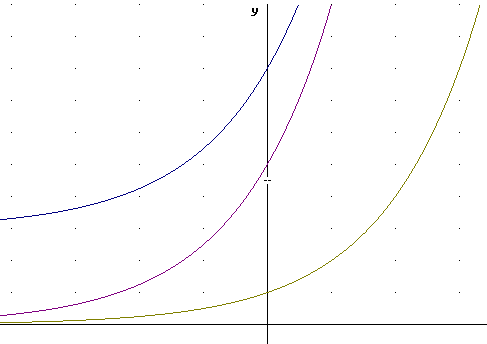
First apply the -5, which shifts every point 5 units to the right.

The basic points (-1, 1/2), (0, 1) and (1, 2) are transformed by this horizontal shift to (4, 1), (5, 0) and (6, 1).  The function at this point is h(t-5).

Then apply the 2, which vertically stretches the graph so that the preceding basic points become (4, 2), (5, 0) and (6, 2). 

The function we end up with is 2 h(t-5).

The figure below depicts h(t), h(t-5) and 2 h(t-5).

• 3 2^(t-2) + 5

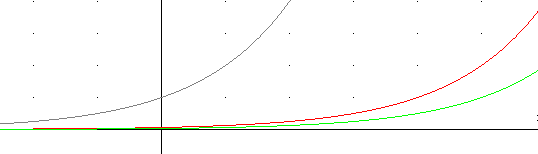
This function shifts 2 units in the t direction, then stretches by factor 3 then shifts +5 units in the vertical direction.

The function is 3 h(t) + 5.

Basic points go from (-1, 1), (0, 0), (1, 1) to (1, 1), (2, 0), (3, 1) to (1, 3), (2, 0), (3, 3) and finally to (1, 8), (2, 5), (3, 8).

The graphs of the original, intermediate and final functions are shown below: