
Properties of exponents are related to properties of logarithms
y = log(x) is the inverse of y = 10^x
ln(x) should be equal to log(x) / log(e).
solve the equation log(y) = 3 log(x) + .699.
process for linearizing and obtaining an equation for the original function
To see why log(ab) = log(a) + log(b)
solve the equation 5^(7x-3) = 14
The equation 2^(3x - 4) + 2^(5x - 1) = 7
The equation 2^(1/x) = 7 * 2^(x+2)
log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4.
Quiz 0406
Tell which of the following are true and identify which are not, and explain why:
a^(b * c) = a^b * c. Not so. Check it out with a = 2, b = 3, c = 4.
a^(b * c) = a^b * a^c. Not so. a^b * a^c = a^(b + c).
a^(b * c) = (a^b)^c. This is so. Check your worksheets for an explanation.
a^(b * c) = a^(b^c). Not so. Check it out with a = 2, b = 3, c = 4.
a^(b * c) = a^b + a^c. Not so. Check it out with a = 2, b = 3, c = 4, and note that for example if b < c we can factor a^b out of a^b + a^c to get a^b(1 + a^(c-b) ).
None of the following is true. Each looks like something else that's true, but ain't. Check with a=2, b=3, c=4 and also figure out what true statement each is mimicking.
a^(b^c) = (a^b)^c
a^(b^c) = a^b * a^c
a^(b^c) = a^(b*c)
a^(b * c) = a^b + a^c
a^(b+c) = a^b + a^c
a^(b+c) = a^b * a^c. This is true because a^b means to multiply a by itself b times, and a^c means to multiply a by itself c times. When you multiply a^b by a^c you end up multiplying a by itself b+c times.
a^(b+c) = (a^b)^c
a^(b+c) = a^b + c
a^(b-c) = a^b - a^c
a^(b-c) = a^b / c
a^(b-c) = a^b / a^c. This one is true for the reason given by the next and the fact that a^(-c) = 1 / a^c.
a^(b-c) = a^b * a^(-c). a^(b-c) = a^(b + (-c)) = a^b * a^(-c).
a^b * a^c = a^(b * c)
a^b * a^c = a^(b + c). a mult by itself b times, mult by a mult by itself c times, gives us a mult by itself b + c times. None of the others is true, as is easily verified by testing and/or by reasoning, and also because none of the others matches the correct result a^(b+c).
a^b * a^c = a^b * c
a^b * a^c = (a^b)^ c
a^b * a^c = a^(b^c)
Make a table of y = 10^x for x = -3, -2, -1, 0, 1, 2, 3 and then reverse columns to form a table of y = log(x).
Using your table find or if necessary estimate the following. No calculators!
log(10^3 * 10^-2) = log(10^1) = 1.
log(10^3) = 3 and log(10^-2) = -2. So we see that
log(10^3 * 10^-2) = log(10^3) + log(10^-2) = 3 - 2 = 1.
Lesson: In the first line we used the laws of exponents to add the exponents of 10, giving us the final exponent of 10. The log is the exponent of 10, so we essentially found the log by adding the exponents.
In the third line the logs of the two numbers are the exponents of 10, and we directly added the exponents to get the log of the product.
The law illustrated here is
log(a*b) = log(a) + log(b),
which is true because the exponent of the product of two powers of the same base is the sum of the exponents, i.e., because 10^(a+b) = 10^b * 10^c.
The table quickly shows us that x = .01 or x = 10^-2.
If the log of a number is 2 then the number is 100. If the number is x^2 then x^2 = 100 and x = 10 or x = -10.
Lesson: In general log(x^2) = 2 * log(x). Even more generally
log(a^b) = b * log(a), which is related to another law of exponents.
10^3 / 10^2 = 10^3-2) = 10^1, so log(10^3 / 10^2) = log(10^1) = 1.
General rule: log(a / b) = log(a) - log(b).
This is directly related to the way the exponents behave, as shown above for log(a*b).
log(10^3) * log(10^2) = 3 * 2 = 6.
This isn't directly related to the fact that 10^3 * 10^2 = 10^5.
log(a) * log(b) isn't directly related to log(a * b).
log(10^3) / log(10^2) = 3 / 2 = 1.5, not directly related to 10^3 / 10^2, which is 10.
log(a) / log(b) isn't directly related to log(a/b), or to a/b.
log(10^3) + log(10^-2) = 3 + (-2) = 1.
Note that 10^3 * 10^-2 = 10^1.
Again, log(a) + log(b) = log(a * b).
During the preceding class we saw that the power function y = 5 x^3 can be linearized with a log(y) vs. log(x) graph, which has slope 3 and y-intercept .699.
This slope and intercept on the log(y) vs. log(x) graph give us the equation log(y) = 3 log(x) + .699.
We will develop the ideas of logarithms and by the end of class we will see how to solve the equation log(y) = 3 log(x) + .699 for y.
We observe that y = log(x) is the inverse of y = 10^x, as can be verified using a calculator.
If we pick any number for x and use the calculator to find 10^x, if we then take the log of this result we get our original number x back.
If we pick any positive number for x and use the calculator to find log(x), if we then raise 10 to the power of this result we get our original number x back.
You should check these claims out using your calculator.
The figure below shows these relationships schematically. We note the following:
y = log x means the same thing as 10^y = x.
y = 10^x means the same thing as log y = x.
We can also say that 10^(log x) = x, and that log(10^x) = x.

The base b logarithm function is the inverse of the b^x function, as indicated in the table below:
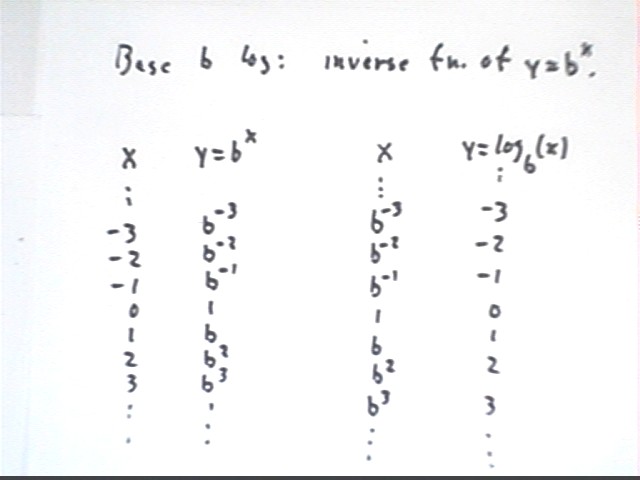
Properties of exponents are related to properties of logarithms, as indicated in the table below.

We can illustrate the law that says that log{base b}(x) = log(x) / log(b) by looking at the relationship between the base-e logarithm ln(x) and the base-10 logarithm log(x):
A table of log(x), ln(x) and log(x) / ln(x) is shown below.
We see that log(x) / ln(x) is always .434, accurate to 3 significant figures.
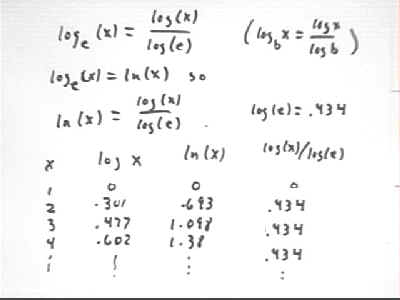
Since ln(x) = log{base e}(x), which by our law is equal to log(x) / log(e), our law tells us that ln(x) should be equal to log(x) / log(e).
You can verify using your calculator that log(e) = log(2.718) is .434 (look again at the table above to see the significance of .434).
Thus log(x) / log(e) = log(x) / .434.
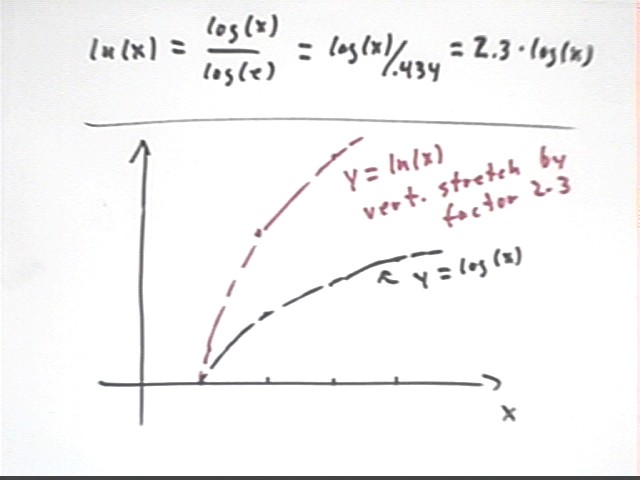
Since 1 / .434 = 2.3, we see that ln(x) = 2.3 * log(x).
This tells us that the function y = ln(x) is a vertical stretch by factor 2.3 of y = log(x).
This relationship is illustrated in the figure below.
We now use the laws of logarithms to solve the equation log(y) = 3 log(x) + .699.
We begin with the equation log(y) = 3 log(x) + .699, and we raise 10 to a power equal to each side of the equation to obtain the equation
10^(log y) = 10 ^ (3 log x + .699).
Since 10^(log y) = y by the inverse-function relationship we obtain
y = 10 ^ (3 log x + .699).
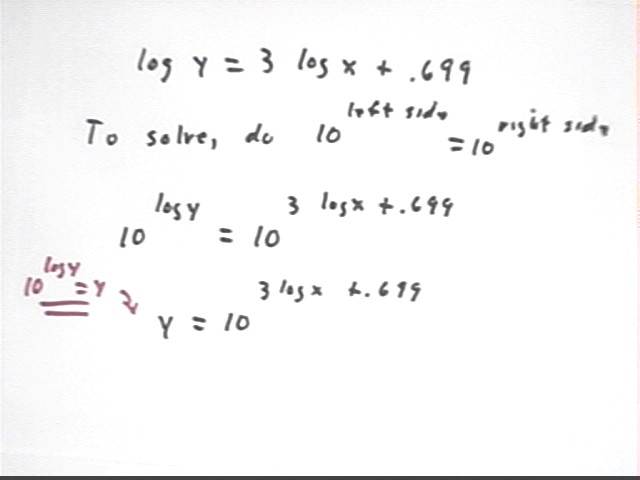
Starting with y = 10 ^ (3 log x + .699) we complete the solution:
Since b^(x+y) = b^x b^y (where x and y are not related to the x and y in the equation) we have 10 ^ ( 3 log x + .699) = 10^(3 log x) * 10^.699 and the equation becomes
y = 10^(3 log x) * 10^.699.
10^.699 is just a number we can evaluate on our calculator. 10^(3 log x) = (10^(log(x) ) ^3, and 10^log(x) = x so (10^(log(x) ) ^3 = x^3 and we now have
y = x ^ 3 * 10^.699.
Evaluating 10^.699 we obtain 5 so our final equation is
y = 5 x^3.
Note that this is the equation we linearized in the previous class to obtain the equation we just solved. So we've come full circle. The process for linearizing and obtaining an equation for the original function was:
Linearize the data.
Get the equation of the linearized data.
Solve that equation for y.
In this example we knew the function y = 5 x^3 to start with. Had we not known that the data follows from this equation, we would have found the equation anyway.
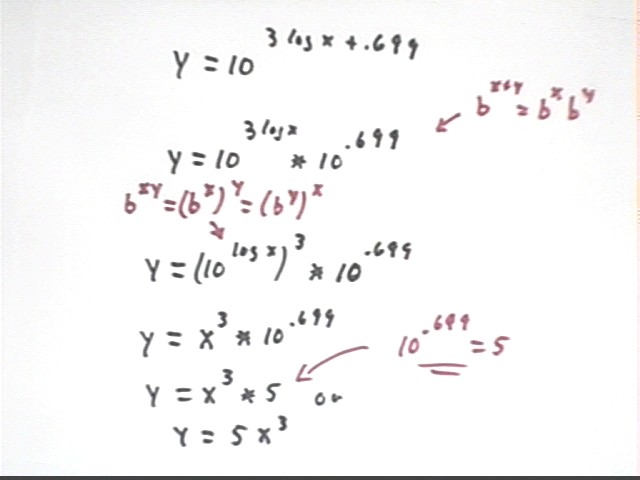
We note that a formula can 'look right' but be very wrong. Be sure to always check out your operations on logarithms with the laws.
log(x+y) looks like log oughtta distribute over x + y, but there is no reason at all so suppose it does. We might call this the 'fallacy of linearity'. log(x+y) emphatically does not equal log(x) + log(y). Among other things log(x) + log(y) = log(xy), not log(x+y).
log(ab) does not equal b log(a). Among other things b log(a) = log(a^b).
(log a)^b is not log(ab). log(ab) = log(a) + log(b), not (log a)^b.
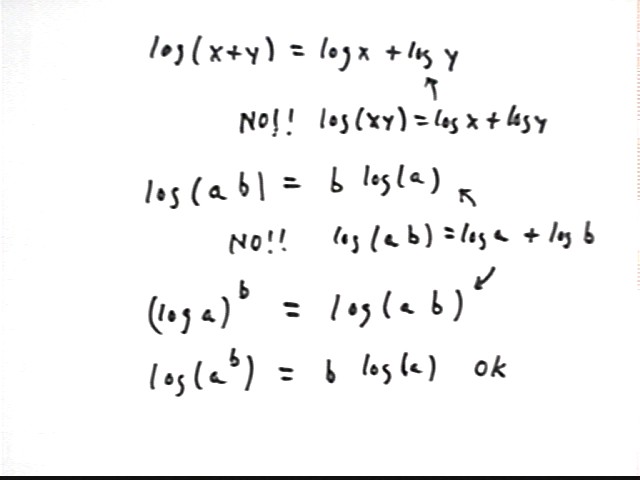
To see why log(ab) = log(a) + log(b), first note that 10(x+y) = 10^x * 10^y, from which it follows that log(10^(x+y) ) = log(10^x * 10^y) = log(10^x) + log(10^y) = x + y.
Whatever a and b are, each can be expressed as a power of 10. If a = 10^x and b = 10^y, which is the case for some x and some y, then log(ab) = x + y. But since a = 10^x, log a = x and since b = 10^y, log b = y, so x + y = log a + log b. It follows that log(ab) = log(a) + log(b).
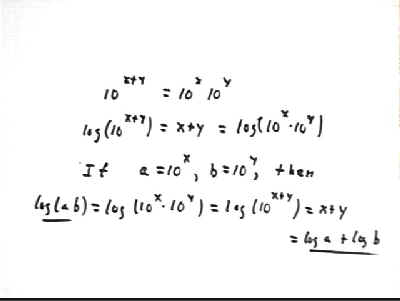
Note that log{base b}(x) is the power of b required to get x.
e.g., log{base 2}(8) is the power of 2 necessary to get 8. Since 2^3 = 8, log{base 2}(8) = 3.
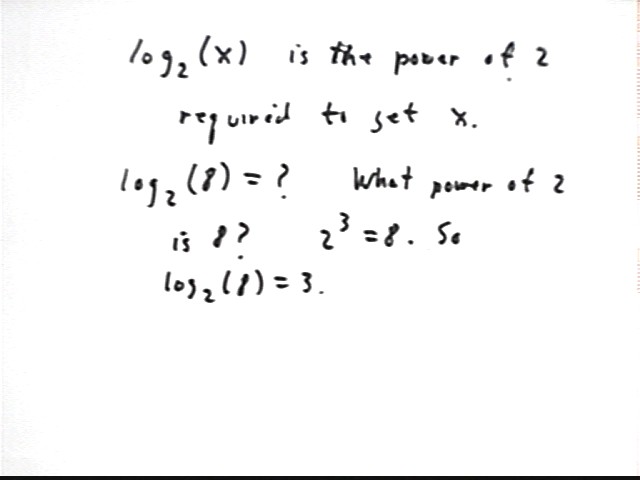
log{base 2}(16) is the power of 2 we need to get 16.
Trial and error tells us that 2^4 = 16 so log{base 2}(16) = 4.
log{base 3}(81) is the power of 3 we need to get 81.
Trial and error tells us that 3^4 = 81 so log{base 3}(81) = 4.
log{base 5}(125) is the power of 5 we need to get 125.
Trial and error tells us that 5^3 = 125 so log{base 5}(125) = 3.
log{base 4}(64) is the power of 4 we need to get 64.
Trial and error tells us that 4^3 = 64 so log{base 4}(64) = 3.
log{base 4}(32). 4^2 = 16 and 4^3 = 64. So log{base 4}(32) is between 2 and 3.
Observe that 4^2 * 2 = 32, and that 2 = 4^(1/2). So
32 = 4^2 * 4^(1/2) = 4^(2.5) or 4(^5/2). So
log{base 4}(32) = 2.5 or 5/2.
log{base 8}(32). We need the power of 8 that is equal to 32.
We note that 8^(1/3) = 2, and 2^5 = 32. So
8^(1/3)^5 = 8^(5/3). Thus
log{base 8}(32) = 5/3.
Suggested problems:
log{base 25}(125)
log{base 9}(243)
log{base 16}(32)
log{base 27}(243)
log{base 2}(16) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 2}(16) = log(16) / log(2) = 4.
log{base 3}(81) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 3}(81) = log(81) / log(3) = 4.
log{base 5}(125) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 5}(125) = log(125) / log(5) = 3.
log{base 4}(64) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 4}(64) = log(64) / log(4) = 3.
log{base 4}(32) is 2.5.
log{base 4}(32) = log(32) / log(4) = 2.5.
log{base 8}(32).
log{base 8}(32) = log(32) / log(8) = 1.66666... .
We solve the equation 5^(7x-3) = 14.
Since our variable x is in the numerator we take the log of both sides to get x out of that numerator, allowing us to use standard algebra to find x.
In the fourth step we have divided both sides by log 5.
In the fifth step we add 3 to both sides.
In the sixth step we multiply both sides by 1/7 and evaluate the resulting expression to find x.
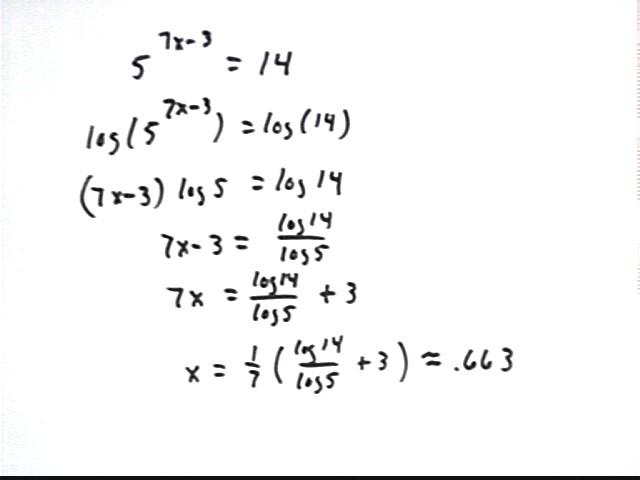
The equation 2^(3x - 4) + 2^(5x - 1) = 7 looks like it should be amenable to the same treatment as in the preceding problem. Taking logs of both sides looks like it should bring the x terms out of the numerator. However there is a serious pitfall in the way of this strategy.
The problem is that log(a+b) is not equal to log a + log b, as we saw earlier. So if after writing
log [2^(3x - 4) + 2^(5x - 1)] = log(7)
we try to say that log(2^(3x-4)) + log(2^(5x - 1) ) = log(7), we are falling into the fallacy of linearity described earlier.
It turns out that this problem cannot be solved to find an exact value of x. We can always approximate the solution, but there is no way to find an exact solution.
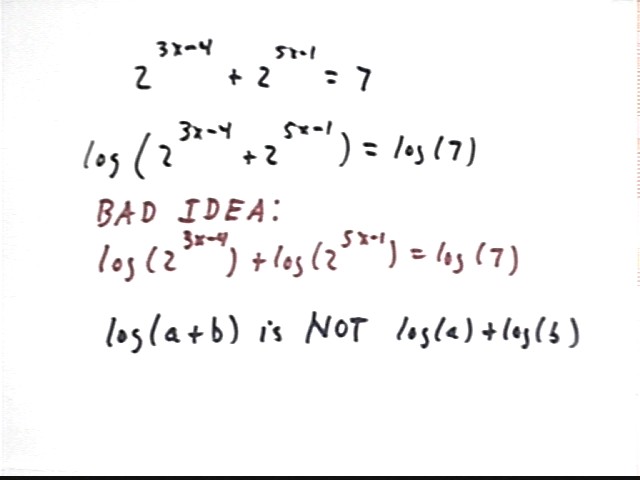
The equation 2^(1/x) = 7 * 2^(x+2) can be solved by taking the log of both sides.
Applying the laws of logarithms we note that log(2^(1/x)) = 1/x * log 2 and log(7 * 2^(x+2) ) = log 7 + log(2^(x+2) and obtain the equation in the third step.
log(2^(x+2) ) = (x + 2) log 2, giving us the equation in the fourth step.
This equation has one denominator, x. Multiplying both sides by this denominator and simplifying gives us that last two steps in the figure below.
The problem is continues on the next figure.
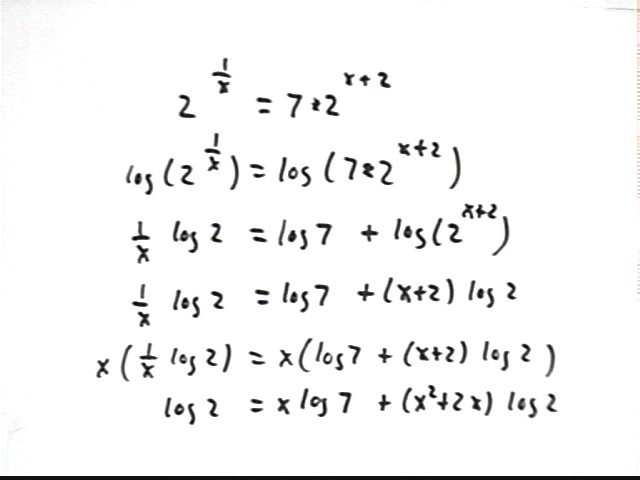
Be sure to understand that log 2 and log 7 are just numbers, which we can easily evaluate using calculators.
We can now see that our equation is quadratic in x, containing x^2, x and constant terms. We will put this equation into the form a x^2 + b x + b and then we will apply the quadratic formula so find values of x which satisfy the equation.
The third line below shows the result of swapping sides and using the distributive law on the expression (x^2 + 2x) log 2.
The fourth line puts x^2, x and constant terms in order, with the log 2 from the right side now appearing as the constant - log 2 on the left. We have also factored x out of the two terms containing just the first power of x.
The fourth line is of form a x^2 + b x + c, with a, b and c as specified below.
We choose to approximate a, b and c before plugging into the quadratic.

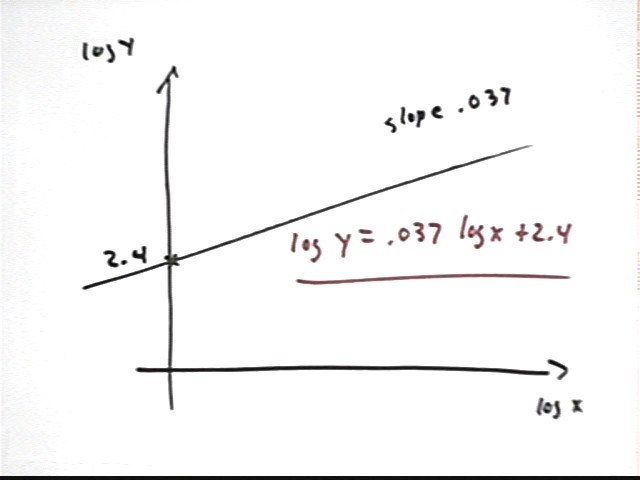
Suppose that in linearizing a data set we find that log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4. What is the function that models our data?
Our straight line has equation log(y) = .037 log(x) + 2.4. Note that it is important to label the axes with the quantities they actually represent; it would be a very bad idea to label the vertical axis y and the horizontal axis x, since the quantities plotted on those axes are in fact log y and log x.
We want to solve this equation for y.
To solve the equation log(y) = .037 log(x) + 2.4 we first write the equation 10^left side = 10^right side, as shown in the second line.
In the third line we simplify using the fact that 10^(log y) = y, and the law of exponents that tells us that 10^(a+b) = 10^a * 10^b.
In the fourth line we rewrite .037 log x as log(x^.037), using the fact that a log(x) = log(x^a).
In the fifth line we use the fact that 10^x and log x are inverse functions to rewrite 10^(log(x^.037)) as just x^.037.
In the last line we evaluate 10^2.4, obtaining 251.
We finally see that the data is modeled by the equation y = 251 x^.037, which is the power function x^p, with p = .037, vertically stretched by factor 251.
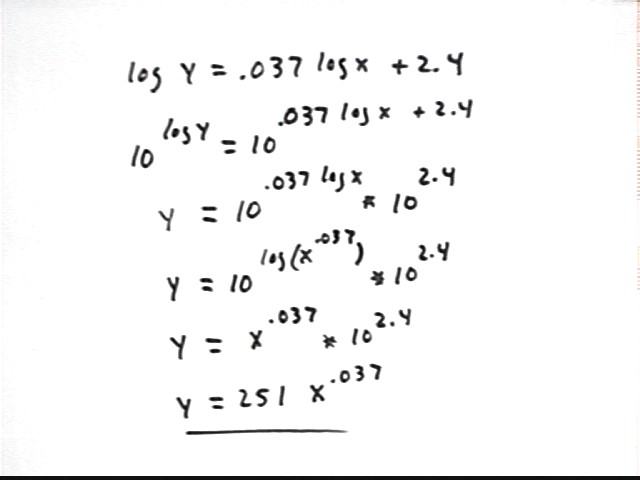
Problem Number 1
What equation would you have to solve to find the doubling time, starting at t = 3, of a population that starts at 1400 organisms and grows at annual rate 8%?
Problem Number 2
Solve using ratios instead of functional proportionalities:
If there are 3.888 billion grains of sand exposed on the surface of the first sand pile, how many grains of sand we expect to be exposed on the surface of the second?
Problem Number 3
If a(n) = a(n-1) + 5, with a(1) = 7, then what is the value of a( 330)?
Problem Number 4
If a door spring has a length that changes linearly with the weight supported as long as the spring's length is at least 44 cm, what is the linear function weight(load) that models the length, provided that the length is 80 cm when the load is 1.58 pounds, and that the length changes at a rate of .05 cm / pound?
Problem Number 5
Problem: Obtain a quadratic depth vs. clock time model if depths of 28.057 cm, 19.79825 cm and 15.22374 cm are observed clock times t = 9.846519, 19.69304 and 29.53955 seconds.
Problem: The quadratic depth vs. clock time model corresponding to depths of 28.057 cm, 19.79825 cm and 15.22374 cm at clock times t = 9.846519, 19.69304 and 29.53955 seconds is depth(t) = .019 t2 + -1.4 t + 40. Use the model to determine whether the depth will ever reach zero.
Problem Number 6
Find the vertex and the zeros of y = .028 t2 + -1.6 t + 79.
Problem Number 7
If y = 2 t^2 + 11 t + -95, what symbolic expression stands for the slope between the graph points for which t = x and t = x+h?
Problem Number 8
Find the equation of a line through ( 7, 3) and ( 3, 9) by each of the following methods:
If your graph represents the velocity of a coasting automobile, in mph, vs. clock time in seconds: