
Quiz 0408
The primary laws of logarithms include
log(a*b) = log(a) + log(b),
log{base b}(a) = log a / log b,
10^log(x) = x and
log(a^b) = b * log(a).
solve the equation log(y) = 3 log(x) + .699.
1. Solve for y the equation log(y) = 3 log(x) + .699. First rewrite the equation as 10^left-hand side = 10^right-hand side. Then use the laws of logarithms to simplify.
2. Solve the following equations, where it is possible to do so:
5^(7x-3) = 14
solve the equation 5^(7x-3) = 14
2^(3x - 4) + 2^(5x - 1) = 7
The equation 2^(3x - 4) + 2^(5x - 1) = 7
2^(1/x) = 7 * 2^(x+2)
The equation 2^(1/x) = 7 * 2^(x+2)
When linearizing a certain data set log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4. Write the corresponding equation and solve it for y.
log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4.
When linearizing a certain data set log(y) vs. x gives us a straight line with slope -.025 and vertical intercept 12. Write the corresponding equation and solve it for y.
Write the corresponding equation and solve it for y
Properties of exponents are related to properties of logarithms
y = log(x) is the inverse of y = 10^x
ln(x) should be equal to log(x) / log(e).
process for linearizing and obtaining an equation for the original function
To see why log(ab) = log(a) + log(b)
During the preceding class we saw that the power function y = 5 x^3 can be linearized with a log(y) vs. log(x) graph, which has slope 3 and y-intercept .699.
This slope and intercept on the log(y) vs. log(x) graph give us the equation log(y) = 3 log(x) + .699.
We will develop the ideas of logarithms and by the end of class we will see how to solve the equation log(y) = 3 log(x) + .699 for y.
We observe that y = log(x) is the inverse of y = 10^x, as can be verified using a calculator.
If we pick any number for x and use the calculator to find 10^x, if we then take the log of this result we get our original number x back.
If we pick any positive number for x and use the calculator to find log(x), if we then raise 10 to the power of this result we get our original number x back.
You should check these claims out using your calculator.
The figure below shows these relationships schematically. We note the following:
y = log x means the same thing as 10^y = x.
y = 10^x means the same thing as log y = x.
We can also say that 10^(log x) = x, and that log(10^x) = x.

The base b logarithm function is the inverse of the b^x function, as indicated in the table below:
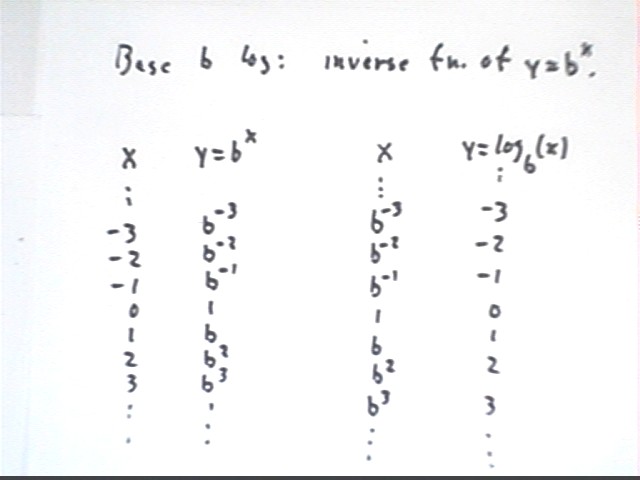
Properties of exponents are related to properties of logarithms, as indicated in the table below.

We can illustrate the law that says that log{base b}(x) = log(x) / log(b) by looking at the relationship between the base-e logarithm ln(x) and the base-10 logarithm log(x):
A table of log(x), ln(x) and log(x) / ln(x) is shown below.
We see that log(x) / ln(x) is always .434, accurate to 3 significant figures.
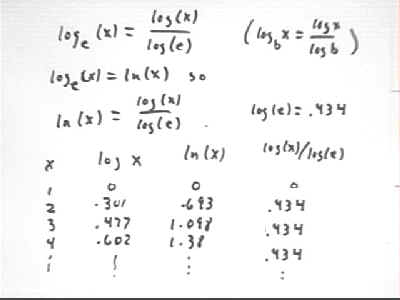
Since ln(x) = log{base e}(x), which by our law is equal to log(x) / log(e), our law tells us that ln(x) should be equal to log(x) / log(e).
You can verify using your calculator that log(e) = log(2.718) is .434 (look again at the table above to see the significance of .434).
Thus log(x) / log(e) = log(x) / .434.
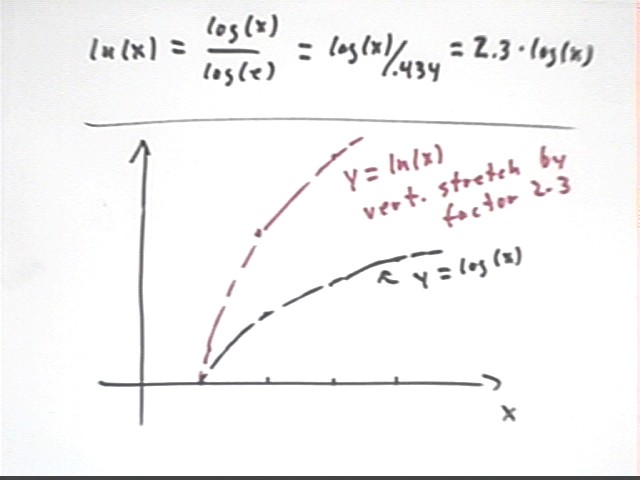
Since 1 / .434 = 2.3, we see that ln(x) = 2.3 * log(x).
This tells us that the function y = ln(x) is a vertical stretch by factor 2.3 of y = log(x).
This relationship is illustrated in the figure below.
We now use the laws of logarithms to solve the equation log(y) = 3 log(x) + .699.
We begin with the equation log(y) = 3 log(x) + .699, and we raise 10 to a power equal to each side of the equation to obtain the equation
10^(log y) = 10 ^ (3 log x + .699).
Since 10^(log y) = y by the inverse-function relationship we obtain
y = 10 ^ (3 log x + .699).
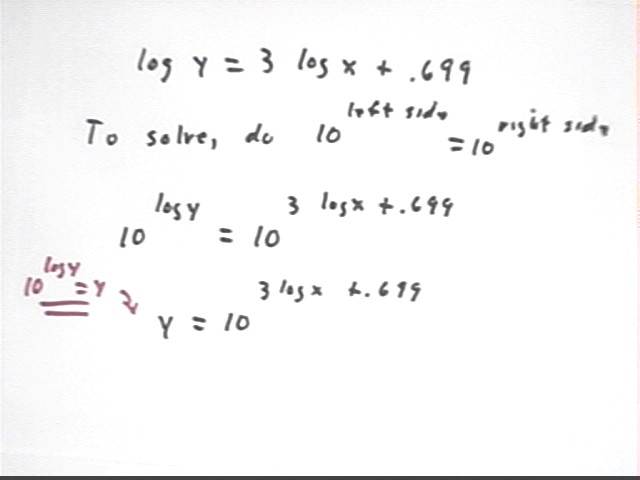
Starting with y = 10 ^ (3 log x + .699) we complete the solution:
Since b^(x+y) = b^x b^y (where x and y are not related to the x and y in the equation) we have 10 ^ ( 3 log x + .699) = 10^(3 log x) * 10^.699 and the equation becomes
y = 10^(3 log x) * 10^.699.
10^.699 is just a number we can evaluate on our calculator. 10^(3 log x) = (10^(log(x) ) ^3, and 10^log(x) = x so (10^(log(x) ) ^3 = x^3 and we now have
y = x ^ 3 * 10^.699.
Evaluating 10^.699 we obtain 5 so our final equation is
y = 5 x^3.
Note that this is the equation we linearized in the previous class to obtain the equation we just solved. So we've come full circle. The process for linearizing and obtaining an equation for the original function was:
Linearize the data.
Get the equation of the linearized data.
Solve that equation for y.
In this example we knew the function y = 5 x^3 to start with. Had we not known that the data follows from this equation, we would have found the equation anyway.
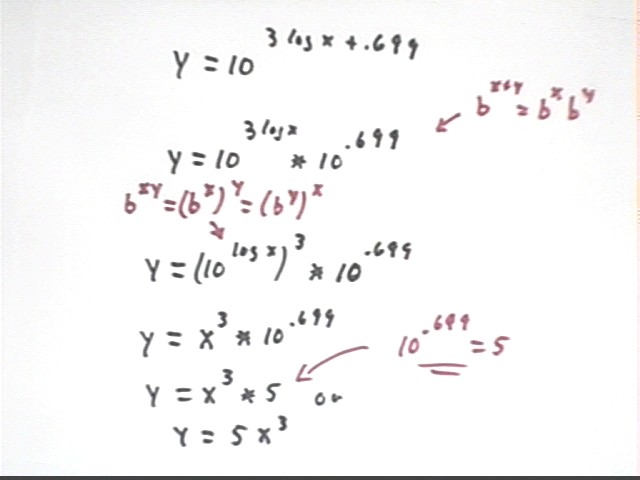
We note that a formula can 'look right' but be very wrong. Be sure to always check out your operations on logarithms with the laws.
log(x+y) looks like log oughtta distribute over x + y, but there is no reason at all so suppose it does. We might call this the 'fallacy of linearity'. log(x+y) emphatically does not equal log(x) + log(y). Among other things log(x) + log(y) = log(xy), not log(x+y).
log(ab) does not equal b log(a). Among other things b log(a) = log(a^b).
(log a)^b is not log(ab). log(ab) = log(a) + log(b), not (log a)^b.
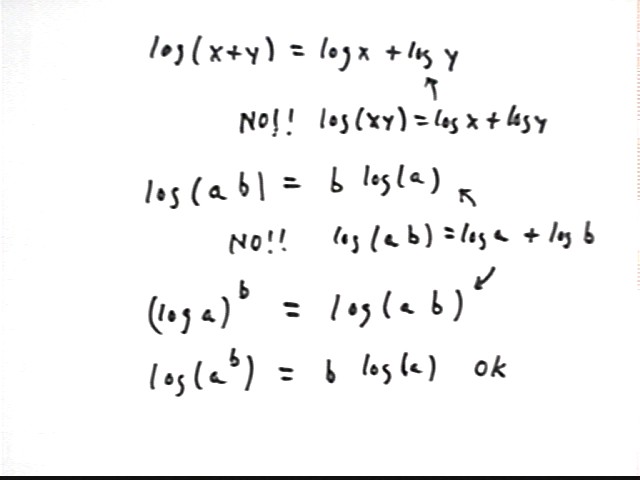
To see why log(ab) = log(a) + log(b), first note that 10(x+y) = 10^x * 10^y, from which it follows that log(10^(x+y) ) = log(10^x * 10^y) = log(10^x) + log(10^y) = x + y.
Whatever a and b are, each can be expressed as a power of 10. If a = 10^x and b = 10^y, which is the case for some x and some y, then log(ab) = x + y. But since a = 10^x, log a = x and since b = 10^y, log b = y, so x + y = log a + log b. It follows that log(ab) = log(a) + log(b).
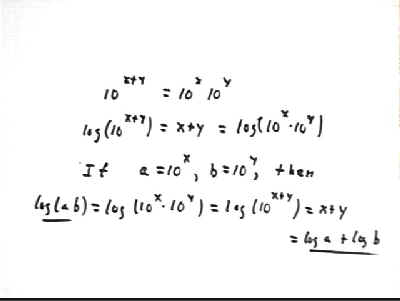
Note that log{base b}(x) is the power of b required to get x.
e.g., log{base 2}(8) is the power of 2 necessary to get 8. Since 2^3 = 8, log{base 2}(8) = 3.
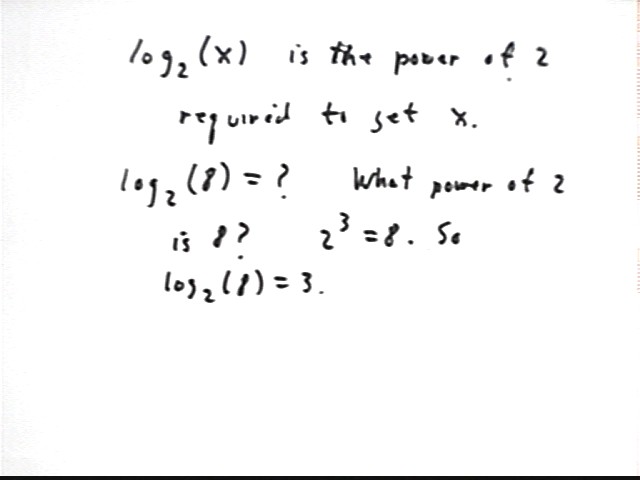
log{base 2}(16) is the power of 2 we need to get 16.
Trial and error tells us that 2^4 = 16 so log{base 2}(16) = 4.
log{base 3}(81) is the power of 3 we need to get 81.
Trial and error tells us that 3^4 = 81 so log{base 3}(81) = 4.
log{base 5}(125) is the power of 5 we need to get 125.
Trial and error tells us that 5^3 = 125 so log{base 5}(125) = 3.
log{base 4}(64) is the power of 4 we need to get 64.
Trial and error tells us that 4^3 = 64 so log{base 4}(64) = 3.
log{base 4}(32). 4^2 = 16 and 4^3 = 64. So log{base 4}(32) is between 2 and 3.
Observe that 4^2 * 2 = 32, and that 2 = 4^(1/2). So
32 = 4^2 * 4^(1/2) = 4^(2.5) or 4(^5/2). So
log{base 4}(32) = 2.5 or 5/2.
log{base 8}(32). We need the power of 8 that is equal to 32.
We note that 8^(1/3) = 2, and 2^5 = 32. So
8^(1/3)^5 = 8^(5/3). Thus
log{base 8}(32) = 5/3.
Suggested problems:
log{base 25}(125)
log{base 9}(243)
log{base 16}(32)
log{base 27}(243)
log{base 2}(16) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 2}(16) = log(16) / log(2) = 4.
log{base 3}(81) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 3}(81) = log(81) / log(3) = 4.
log{base 5}(125) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 5}(125) = log(125) / log(5) = 3.
log{base 4}(64) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 4}(64) = log(64) / log(4) = 3.
log{base 4}(32) is 2.5.
log{base 4}(32) = log(32) / log(4) = 2.5.
log{base 8}(32).
log{base 8}(32) = log(32) / log(8) = 1.66666... .
We solve the equation 5^(7x-3) = 14.
Since our variable x is in the numerator we take the log of both sides to get x out of that numerator, allowing us to use standard algebra to find x.
In the fourth step we have divided both sides by log 5.
In the fifth step we add 3 to both sides.
In the sixth step we multiply both sides by 1/7 and evaluate the resulting expression to find x.
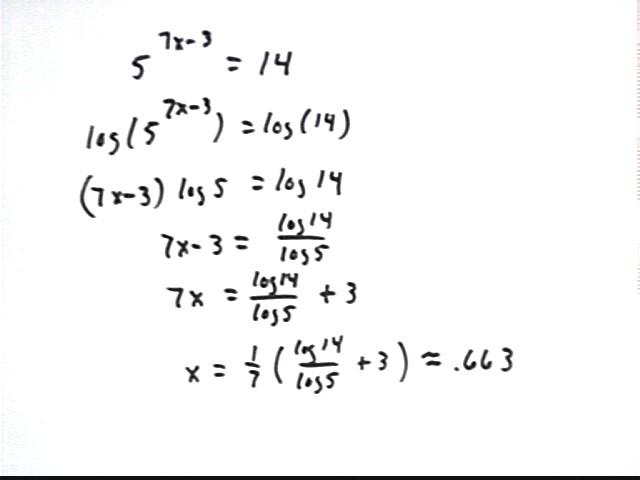
The equation 2^(3x - 4) + 2^(5x - 1) = 7 looks like it should be amenable to the same treatment as in the preceding problem. Taking logs of both sides looks like it should bring the x terms out of the numerator. However there is a serious pitfall in the way of this strategy.
The problem is that log(a+b) is not equal to log a + log b, as we saw earlier. So if after writing
log [2^(3x - 4) + 2^(5x - 1)] = log(7)
we try to say that log(2^(3x-4)) + log(2^(5x - 1) ) = log(7), we are falling into the fallacy of linearity described earlier. That is, log(a) + log(b) = log(a * b), so log(a+b) is not log(a) + log(b).
It turns out that this problem cannot be solved to find an exact value of x. We can always approximate the solution, but there is no way to find an exact solution.
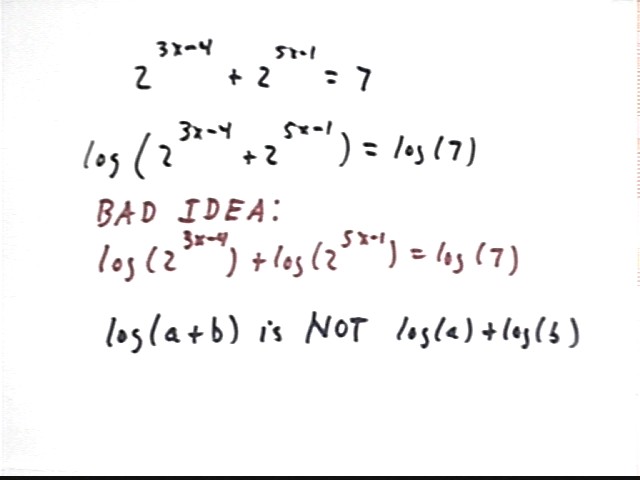
The equation 2^(1/x) = 7 * 2^(x+2) can be solved by taking the log of both sides.
Applying the laws of logarithms we note that log(2^(1/x)) = 1/x * log 2 and log(7 * 2^(x+2) ) = log 7 + log(2^(x+2) and obtain the equation in the third step.
log(2^(x+2) ) = (x + 2) log 2, giving us the equation in the fourth step.
This equation has one denominator, x. Multiplying both sides by this denominator and simplifying gives us that last two steps in the figure below.
The problem is continues on the next figure.
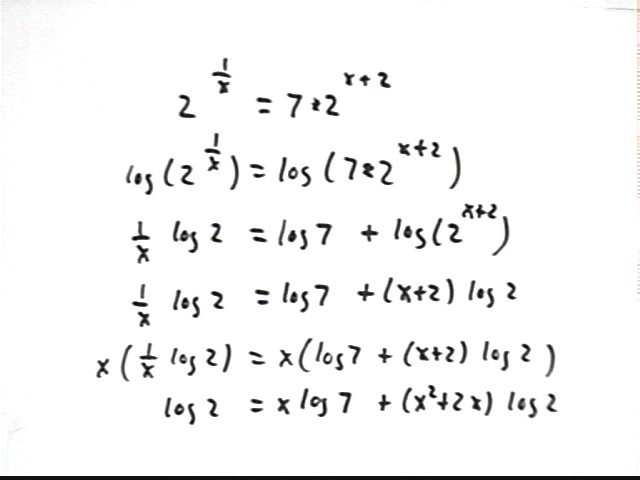
Be sure to understand that log 2 and log 7 are just numbers, which we can easily evaluate using calculators.
We can now see that our equation is quadratic in x, containing x^2, x and constant terms. We will put this equation into the form a x^2 + b x + b and then we will apply the quadratic formula so find values of x which satisfy the equation.
The third line below shows the result of swapping sides and using the distributive law on the expression (x^2 + 2x) log 2.
The fourth line puts x^2, x and constant terms in order, with the log 2 from the right side now appearing as the constant - log 2 on the left. We have also factored x out of the two terms containing just the first power of x.
The fourth line is of form a x^2 + b x + c, with a, b and c as specified below.
We choose to approximate a, b and c before plugging into the quadratic.

We could also have solve the equation as follows:
2^(1/x) = 7 * 2^(x+2). Multiply both sides by 2^-(x+2) to get
2^(1/x) * 2^(x-2) = 7 * 2^(x+2) * 2^-(x+2), which simplifies to
2^(1/x - (x+2) ) = 7 and further simplifies to
2^(1/x - x - 2) = 7. Taking the log of both sides we get
log[ 2^(1/x - x - 2) ] = log [ 7 ] so that
[ 1/x - x - 2 ] log 2 = log 7. Multiplying both sides by the denominator x we get
( 1 - x^2 - 2x ) log 2 = x log 7; dividing both sides by log 2 we have
( 1 - x^2 - 2x ) = x log 7 / log 2. Expanding and arranging in descending powers we have
-x^2 - 2x + 1 = x log 7 / log 2. This is a quadratic equation, which we rearrange to get
-x^2 - 2 x - x log 7 / log 2 + 1 = 0. Factoring out the x in the middle two terms we have
-x^2 - (2 + log 7 / log 2) x + 1 = 0. Reversing signs this is
x^2 + (2 + log 7 / log 2) x - 1 = 0. This is the standard form of a quadratic. A decimal approximation of 2 + log 7 / log 2 gives us
x^2 + 4.81 x - 1 = 0. Substituting the coefficients into the quadratic equation gives us the same results as the previous solution.
It is worthwhile to compare this solution with the previous solution in order to see how the laws of exponents and logarithms are used slightly different ways to arrive at the same result.
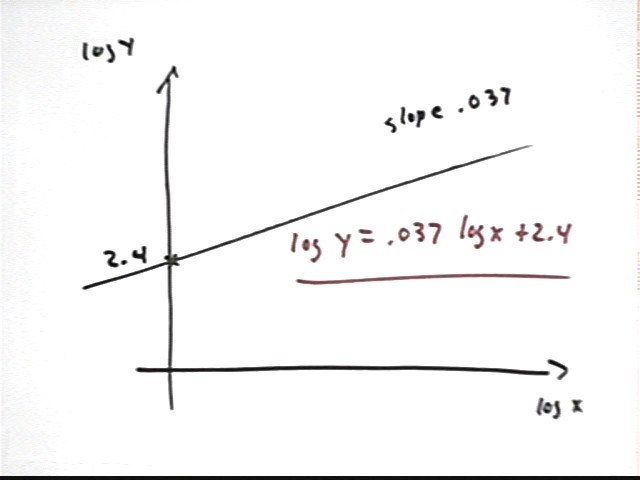
Suppose that in linearizing a data set we find that log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4. What is the function that models our data?
Our straight line has equation
log(y) = .037 log(x) + 2.4.
Note that it is important to label the axes with the quantities they actually represent; it would be a very bad idea to label the vertical axis y and the horizontal axis x, since the quantities plotted on those axes are in fact log y and log x.
We want to solve this equation for y.
To solve the equation log(y) = .037 log(x) + 2.4 we first write the equation 10^left side = 10^right side, as shown in the second line.
In the third line we simplify using the fact that 10^(log y) = y, and the law of exponents that tells us that 10^(a+b) = 10^a * 10^b.
In the fourth line we rewrite .037 log x as log(x^.037), using the fact that a log(x) = log(x^a).
In the fifth line we use the fact that 10^x and log x are inverse functions to rewrite 10^(log(x^.037)) as just x^.037.
In the last line we evaluate 10^2.4, obtaining 251.
We finally see that the data is modeled by the equation y = 251 x^.037, which is the power function x^p, with p = .037, vertically stretched by factor 251.
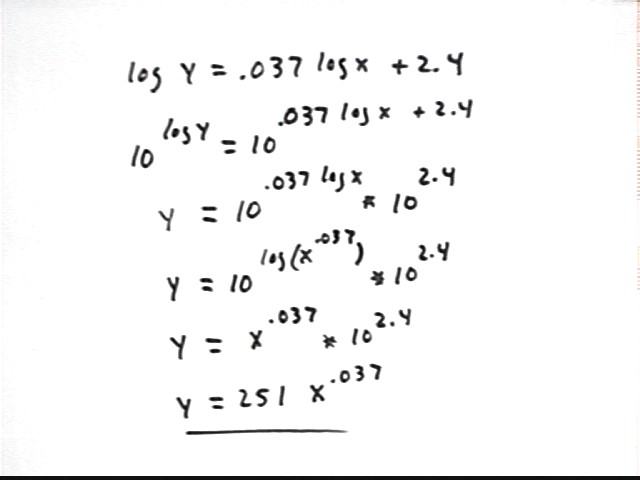
When linearizing a certain data set log(y) vs. x gives us a straight line with slope -.025 and vertical intercept 12. Write the corresponding equation and solve it for y.
The equation is
log(y) = -.025 * x + 12. Using the inverse of the log function we get
10^(log y) = 10^(-.025 x + 12). The inverse function property and the laws of exponents give us
y = 10^12 * 10^(-.025 x). Since a^(bc) = (a^b)^c we have
y = 10^12 * (10^-.025)^ x, which simplifies to give us
y = 10^12 * .94^x, approx..
This is an exponential function with growth factor .94, implying a growth rate of -.06.
Compare this solution with our previous solution of a log y vs. log x linearization. You will see why the former gave us a power function and why this solution gives us an exponential function.
Generalizing, any time log y vs. x is linear we get an exponential function, and any time log y vs. log x is linear we get a power function.
Problem Number 1
What equation would you have to solve to find the doubling time, starting at t = 3, of a population that starts at 1400 organisms and grows at annual rate 8%?
The population function is
The population will double when P(t) reaches double its initial 1400 so the equation is
It's not required with the present statement of the problem but might be on another problem to simplify this equation, which we easily do, dividing both sides by 1400 to get
This equation can then be solved using logs, but that isn't required until the next test.
On this test you could get away with the model obtained if the population function is compounded every year rather that continuously. This would not be correct and it's better to use the correct 'continuously compounded' model P(t) = 1400 e^(.08 t) but at this point we haven't clearly made that distinction so the function
The equation for doubling time would then be
which would simplify to
Problem Number 2
Solve using ratios instead of functional proportionalities:
Mass is proportional to volume, which for geometrically similar objects is proportional to the cube of any given linear dimension. In this case we conclude that mass is proportional to the height.
Thus we have a y = k x^3 proportionality, which as we have seen implies the
x2 and x1 are the diameters, y2 and y1 the masses. We are given x2 = 7.9 m and x1 = 3.6 m, with y1 = 23328 kg and y2 unknown. This gives us
This is the only correct way to use ratios to solve this problem.
Area is covered by little squares so the proportionality is y = k x^2 and the ratio equation is y2 / y1 = (x2 / x1)^2 so that
Problem Number 3
If a(n) = a(n-1) + 5, with a(1) = 7, then what is the value of a( 330)?
a(330) is obtained from a(1) by making 329 'jumps' each of 5 units, resulting in a total 'jump' of 329 * 5 = 1645 units. Starting from a(1) = 7 this puts us at 7 + 1645 = 1652. So a(330) = 1652.
Problem Number 4
If a door spring has a length that changes linearly with the weight supported as long as the spring's length is at least 44 cm, what is the linear function length(load) that models the length, provided that the length is 80 cm when the load is 1.58 pounds, and that the length changes at a rate of .05 cm / pound?
A graph of length vs. load has a slope that is equal to the rate of change of length with respect to load, so the slope is .05 cm / pound.
The y = m x + b form of the equation is therefore
When load is 80 cm the length is 1.58 pounds so we know that
Our final model is therefore
Problem Number 5
Problem: Obtain a quadratic depth vs. clock time model if depths of 28.057 cm, 19.79825 cm and 15.22374 cm are observed clock times t = 9.846519, 19.69304 and 29.53955 seconds.
Plug the three data points into the form y = a t^2 + b t + c and get three simultaneous linear equations in a, b and c. Solve to get a, b and c and plug back into the form to get your model.
Problem: The quadratic depth vs. clock time model corresponding to depths of 28.057 cm, 19.79825 cm and 15.22374 cm at clock times t = 9.846519, 19.69304 and 29.53955 seconds is depth(t) = .019 t2 + -1.4 t + 40. Use the model to determine whether the depth will ever reach zero.
Set .019t^2 - 1.4 t + 40 = 0 and use the quadratic formula to determine whether there are any real solutions. If the discriminant is positive then it has a positive square root and there will be two distinct real solutions. If the discriminant is zero its square root is zero and there is one repeated solution. If the discriminant is negative you cain't take its square root and you get no real solutions.
Problem Number 6
Find the vertex and the zeros of y = .028 t2 + -1.6 t + 79.
The vertex occurs at t = -b / (2a), as indicated by the quadratic formula. The y coordinate of the vertex is obtained by substituting its t coordinate. You need to give both coordinates.
The parabola opens upward since a = .028 is positive. If the vertex is above the t axis there will be no zeros, since the parabola will never intersect the t axis. If the vertex is on the t axis then the parabola intercepts the t axis only at this point and there is exactly one (repeated) zero. If the vertex is below the t axis the parabola will intersect the t axis at two different points and there will be two distinct zeros.
The quadratic formula will confirm this analysis and give us the details, including whether the discriminant is positive, negative or zero and if the discriminant is not negative we will get the t values of the zeros of the function.
Problem Number 7
If y = 2 t^2 + 11 t + -95, what symbolic expression stands for the slope between the graph points for which t = x and t = x+h?
The y coordinates of the t = x and t = x + h points are y = 2 x^2 + 11 x - 95 and y = 2 (x+h)^2 + 11 (x+h) - 95.
The rise between the points is therefore the difference 2 (x+h)^2 + 11 (x+h) - 95 - (2 x^2 + 11 x - 95) of the y coordinates.
The run is the difference x + h - x = h of the t coordinates.
The slope is therefore
We can simplify this expression to get
= (4 x h + 2 h^2 + 11 h) / h
= 4 x + 11 + 2 h.
If we let h approach zero we get a limiting value of 4x + 11. This expresses the rate of change of the original function at t = x.
Problem Number 8
Find the equation of a line through ( 7, 3) and ( 3, 9) by each of the following methods:
The form is y = m x + b. Substituting we get the two equations
Subtracting the first equation from the second we get
Substituting back into the first we get
So our equation is
The graph should show the points (7, 3) and (3, 9), as well as an arbitrary point (x, y) on the graph.
The slope between the first two points is (9 - 3) / (3 - 7) = -3/2. The graph should show the rise and the run between these points.
The rise and run between the first point and (x, y) are (y - 3) and (x - 7). So the slope can also be expressed as (y-3) / (x-7). Setting the two expressions for slope equal we have
This agrees with the first method.
If your graph represents the velocity of a coasting automobile, in mph, vs. clock time in seconds:
The vertical coordinate is the velocity and the horizontal the clock time. The rise therefore represents the change in the velocity in mph and the run represents the change in clock time in seconds. So the slope = rise / run gives us change in vel / change in clock time, which we recognize as the average rate of change of velocity with respect to clock time in mph / second.
Our equation is y = -3/2 x + 27/2, which we rewrite as
Substituting clockTime t = 10 sec we get
Again writing
we substitute 14 mph for velocity to get
Subtracting 27/2 mph from both sides we have