Quiz 0420
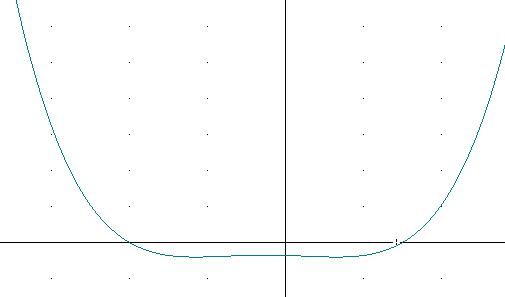
1. We want to graph the polynomial y = (x - 3)(x + 4)(x^2 + x + 6).
The obvious zeros are at x = 3 and x = -4.
The discriminant b^2 - 4 a c of this expression is negative so it doesn't have any zeros.
The zeros at x = 3 and x = -4 come from linear factors so the graph will go through each zero as a nearly straight line.
The x-3 and x+4 factors both give large negatives for large negative x, large positives for large positive x.
x^2 + x + 6 is a large positive whether x is a large positive or a large negative.
For large negatives we therefore have two large negative factors and a large positive factor which gives us a humongous positive result, leading toward W. Va.
Large positives also lead toward W. Va.
We get y = (0 - 3) ( 0 + 4) ( 0^2 + 0 + 6) = -72.

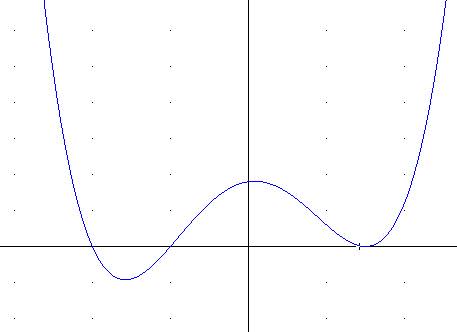
2. Repeat for the function (x-3)(x+4)(x^2 - x - 6).
In this case the x^2 - x - 6 has two zeros, which we can find from the quadratic formula or by factoring. The zeros are at x = 3 and x = -2. The factorization of x^2 - x - 6 is (x-3)(x+2).
So the function is now
y = (x-3)(x+4)(x-3)(x+2) = (x-3)^2(x+4)(x+2).
There is an additional zero at x = -2, and now the zero at x = 3 is quadratic in nature.
The y intercept is now at y = +72.
The graph comes down to the first zero at x = -4 and passes straight through, locally linear, the turns and comes back up through the linear zero at x = 2. The graph then peaks, either to the right or left of the y axis (not clear which at this point) but passes thru (0, 72) on one side or another of the peak. The graph then descends to the quadratic zero at (0, 3), touching the x axis in a locally parabolic shape before going back toward very large positive y values.
3. How many different functions can we make from four linear factors of the form x + a that have zeros at x = 3 and x = -4? One possible combination is (x-3)^2 ( x+4). Write down all possible combinations and quickly sketch a graph for each.
4. On a graph that runs from x = -4 to x = 4, with y values running from -10 to 10, sketch a graph of two straight lines each with slope 1, one having x intercept -2 and one with x intercept +1.
The graph looks like this:
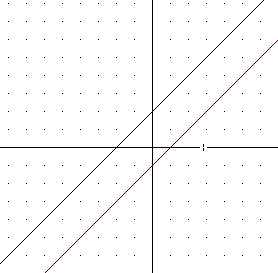
The y coordinates are -1 and -4, easily reasoned out. The sum is -5.
The sum graph would contain the point (-3, -5).
The y coordinates are +1 and -2, giving us a sum of -1.
The sum graph would contain the point (-1, -1).
The y coordinates are +4 and +1, giving us sum 5 and point (2, 5).
The y coordinates are +3 and +6, giving us sum 9 and point (4, 9).
Plotting the points and connecting with a straight line we get the new straight line in the figure below, having slope 2.
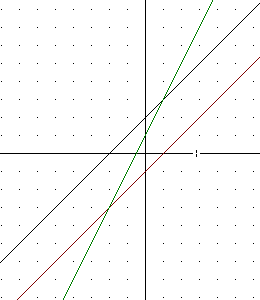
The sum of the y coordinates at x = -3, -1, 2 and 4 are -5, -1, 5 and 9.
The y coordinates of the first graph at these points are -1, 1, 4 and 6.
The sum of the y coordinates isn't the same as the y coordinate of the first line at any of these points.
The sum of the y coordinates will be the same as the y coordinate of the first line when the y coordinate of the second line is 0. That is, you get the same thing when you add zero.
The y coordinate of the second line is zero at x = 1, so at x = 1 the sum of the y coordinates will be the same as the y coordinate of the second line. Thus, the first line and the sum graph cross at the x = 1 point of the first graph.
The graph below includes the vertical line at x = 1 and illustrates how first line and the sum graph cross at the x = 1 point of the first graph, where the y coordinate of the first graph is 0.
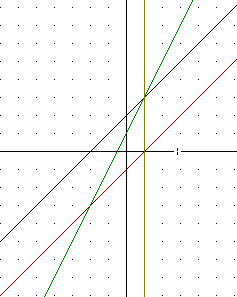
Using the same reasoning as before, this will occur where the y coordinate of the first graph is zero.
The graph below includes the vertical line at x = -2 and illustrates how first line and the sum graph cross at the x = -2 point of the second graph, where the y coordinate of the second graph is 0.
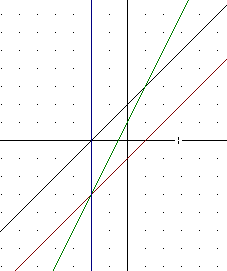
5. Again sketch the two straight lines described in #4.
The y coordinates are -1 and -4, easily reasoned out. The product is +4.
The product graph would contain the point (-3, 4).
The y coordinates are +1 and -2, giving us a product of -2.
The product graph would contain the point (-1, -2).
The y coordinates are +4 and +1, giving us product +4 and point (2, 4).
The y coordinates are +3 and +6, giving us product 18 and point (4, 18).
If we plot the points we have obtained and sketch a smooth curve through the points we get something that looks very much like a parabola, as shown below.
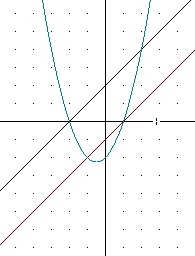
The two graphs represent linear functions. When we multiply two linear functions we get a quadratic function.
Whenever we find the product of two straight-line graphs we will get a parabola.
This occurs when the y coordinate of the first line is 1. You get the same number when you multiply a number by 1.
The y coordinate of the first line is 1 when x = 2, so at x = 2 the product will be equal to the y coordinate of the second graph. We have actually evaluated the product at this point, obtaining the point (2, 4).
We can see that the graph of the product function crosses the graph of the first function at (2, 4).
The figure below includes the horizontal line y = 1 and the vertical line x = 2. These lines intersect at the graph of the second straight line. Be sure you understand why the vertical line x = 2 must therefore intersect the graph of the parabola.
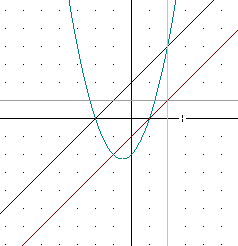
This occurs when the y coordinate of the second line is 1. You get the same number when you multiply a number by 1.
The y coordinate of the second line is 1 when x = -1, so at x = -1 the product will be equal to the y coordinate of the first graph. We have actually evaluated the product at this point, obtaining the point (-1, -2).
We can see that the graph of the product function crosses the graph of the first function at (-1, -2).
The figure below includes the horizontal line y = 1 and the vertical line x = -1. These lines intersect at the graph of the first straight line. Be sure you understand why the vertical line therefore x = -1 must intersect the graph of the parabola.
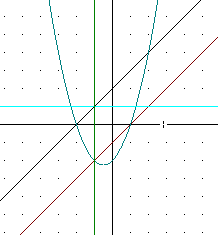
This occurs when either of the y coordinates is zero.
The y coordinate of the first graph is zero when x = -2, so the product function will be 0 when x = -2 and the point (-2, 0) will occur on the graph of the product function. It is clear from the above graphs that the parabola does pass through this point. At this point the parabola intersects the first straight line.
Similarly the product function will be 0 at x = 1, when the second function is zero, and the graph of the product function will therefore intersect the graph of the second straight line at the point (1, 0).
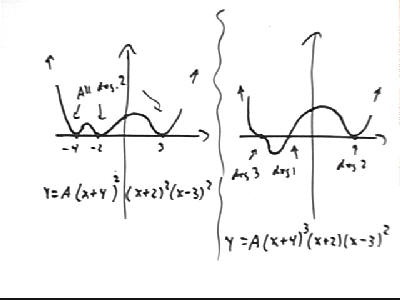
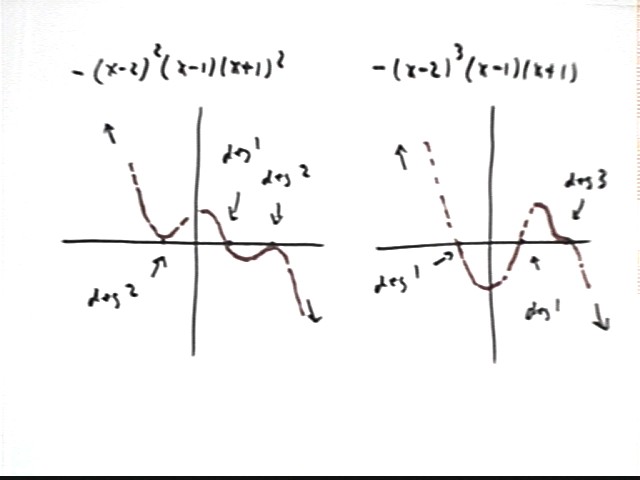
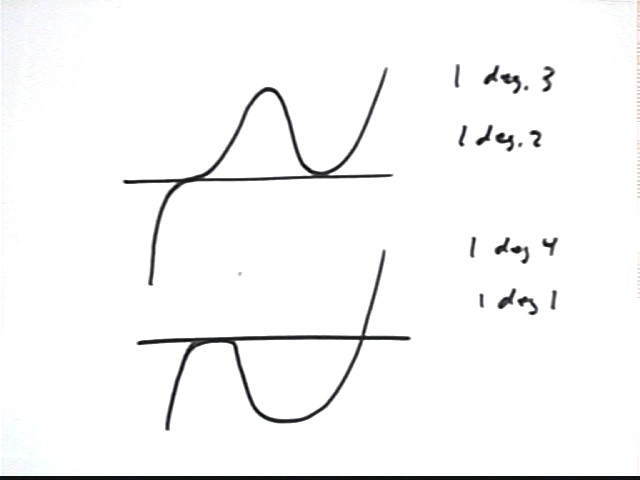
The graphs below both represent a polynomial of degree six with exactly three x value at which we get y = 0.
In the first all zeros are of degree 2, so the graph is very nearly parabolic near these points.
In the second one zero is of degree 3, resulting in a graph that levels off for an instant just as it passes thru the x axis. Another is of degree 1, passing through the x axis in a line which near the zero is very nearly straight, and the other is degree 2, giving us a near-parabola near the zero.
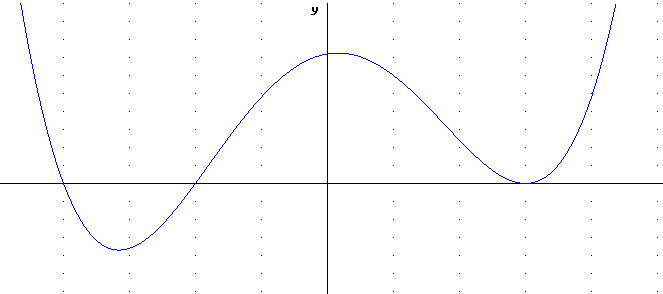
The three graphs below all have exactly three x-intercepts, as in the examples above.
All three also appear to be of even degree, since for large positive as well as large negative x they appear to approach +infinity.
In the graph immediately below the zeros appear to have degrees 1, 1 and 2, indicating a total degree of at least 4.
The next graph appears to have three zeros of degree 2, giving it total degree at least 6.
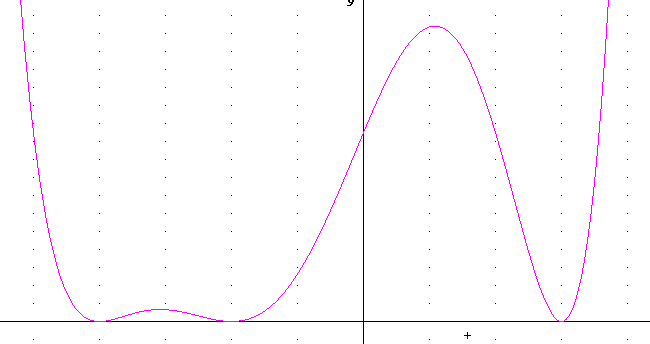
This graph appears to have zeros of degree at least 3, 1 and 2, for total degree at least 6.
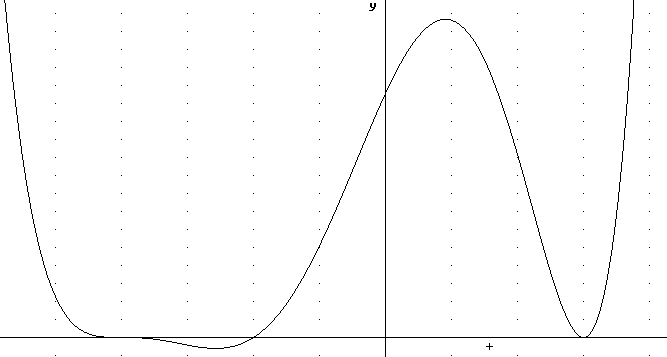
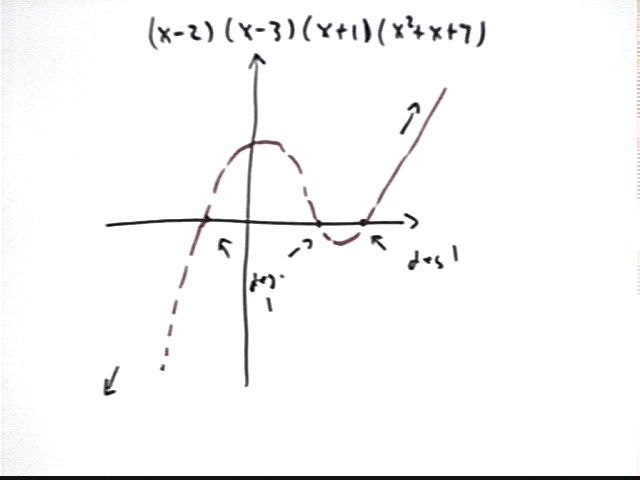
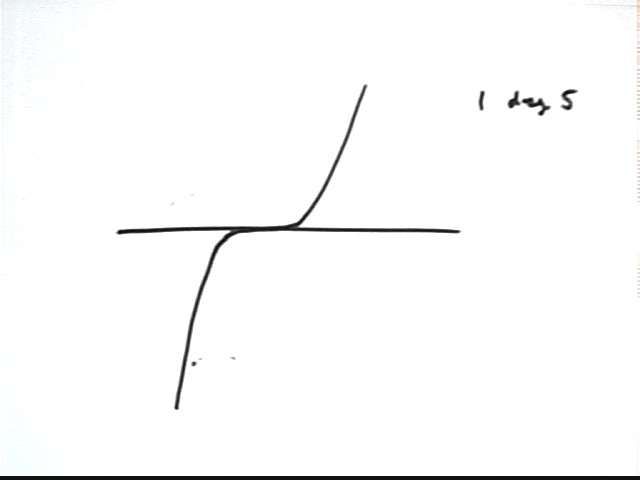
The graph below could represent y = A(x+4)(x+2)(x-3)^2, with its first-degree zeros at x = -4 and x = -2 and its second-degree zero at x = 3.
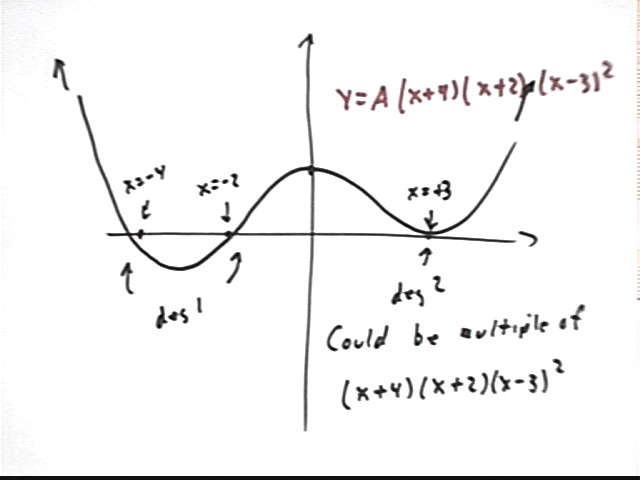
A more accurate graph of this function:

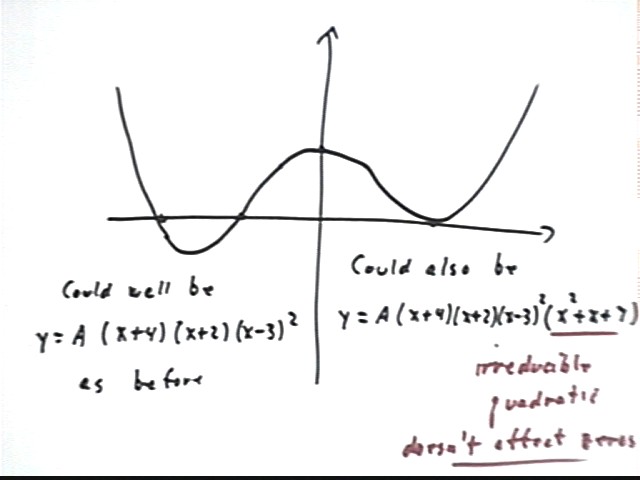
This graph could also conceivably represent y = A(x+4)(x+2)(x-3)^2 * (x^2 + x + 7), because (x^2+x+7) is an arbitrary irreducible quadratic (one we just picked out of a hat containing all irreducible quadratics).
x^2 + x + 7 is an irreducible quadratic because it has no zeros.
If we set x^2 + x + 7 = 0 and try to solve using the quadratic formula our solution will include sqrt(b^2 - 4 a c) = sqrt(1^2 - 4 * 1 * 7) = sqrt(-27), showing that there are no real values of x for which the expression is zero.
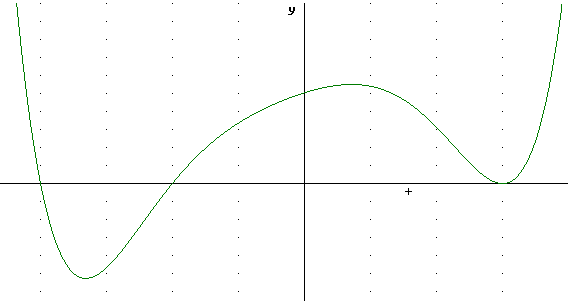
The irreducible quadratic x^2 + x + 7 has vertex at x = -b / (2a) = -1/2. The vertex is its 'low point' so it tends to 'depress' values more near x = -1/2 than away from that point. This causes a little less symmetry in the curve, as opposed to the preceding graph. Note how the curve between x = -2 and x = 3 appears to be a bit more lopsided than in the preceding graph.
Suppose we know that a polynomial has degree 5. What is the maximum number of zeros it could have?
An example of a polynomial of degree 5 might be (x-3)(x-2)(x-1)(x+1)(x+2). This polynomial has 5 zeros, all different. We say that the polynomial has 5 distinct zeros.
If everyone in the class made up their own degree-5 polynomial with no zeros in common with the given polynomial it's very likely that they would all be different.
Suppose we know that a polynomial has degree 5. In how many different ways can we have, say, exactly 3 different numbers that give us zeros?
One possibility would be something like (x-2)^2 (x-1) (x+1)^2, with two of the zeros having degree 2. This polynomial actually has five zeros, since it can be written (x-2)(x-2)(x-1)(x+1)(x+1), but the zeros x = 2 and x = -1 are repeated zeros, each being repeated twice. Thus there are only three different numbers that give us zero, even though there are five zeros.
Another possibility might be of the form (x-2)^3 (x-1)(x+1), with one zero of degree 3 and the other two of degree 1.
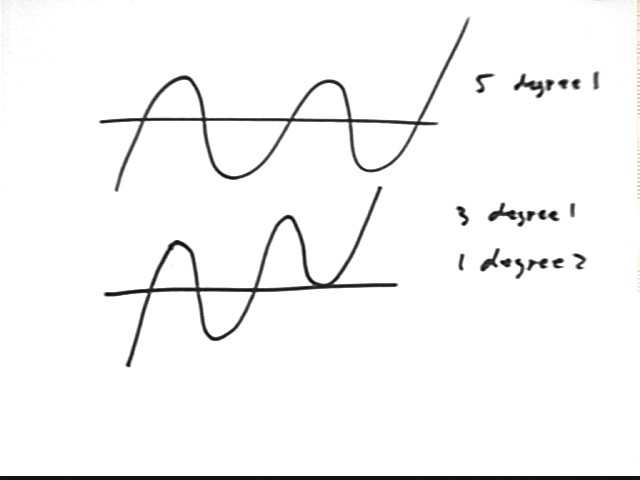
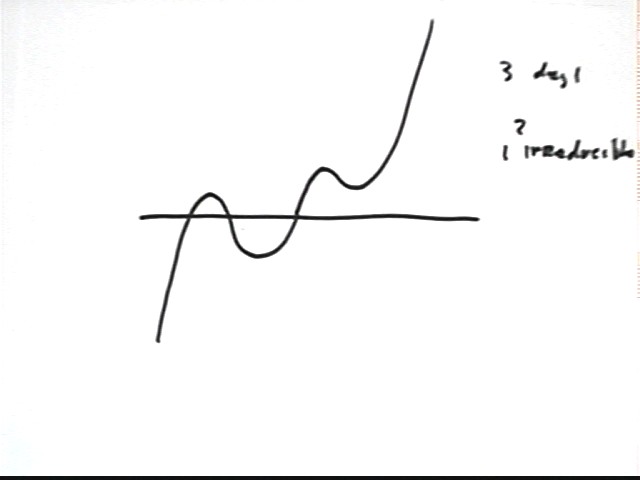
There is one more way we can get a degree-5 polynomial with exactly three different numbers that give us zero. That is to use an irreducible quadratic, as in the example (x-2)(x-3)(x+1)(x^2 + x + 7).
If the zeros are at -2, -1 and 1 then the following are examples of different ways to get polynomials of degree five with exactly three different x values for which the polynomial is zero:
(x-2)^2 (x-1) (x+1)^2
(x-2)^3 (x-1)(x+1)
(x-2)(x-3)(x+1)(x^2 + x + 7)
How can we have a degree 5 polynomial with exactly 4 numbers that give us zero? Sketch such a graph.
We can repeat one of the five zeros, for example getting (x-3)(x-2)^2(x-1)(x+1).
Precalculus I Class 04/10
For a degree-5 polynomial we can have any of the following:
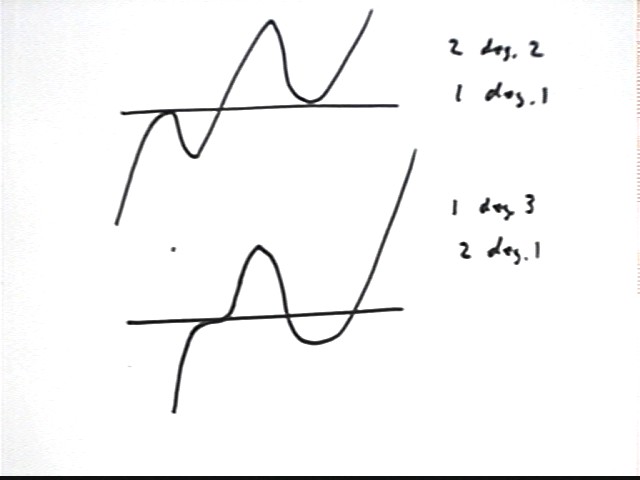
We aren't done yet. We do have a list of every possible combination of five linear factors. However we haven't yet considered what happens if we have an irreducible quadratic (or two).
If there is one irreducible quadratic then we can have
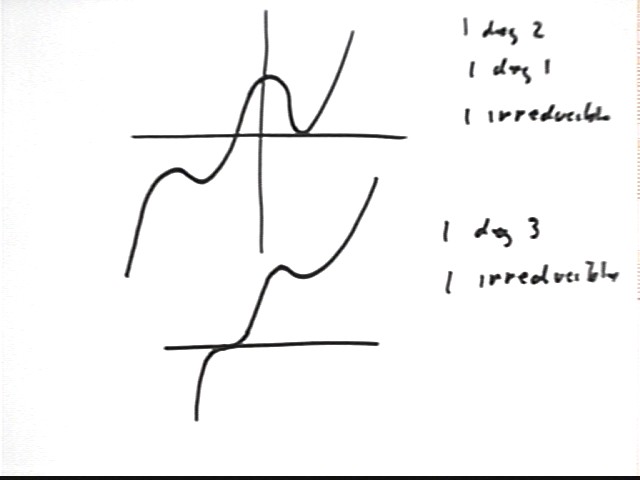
We can also have two irreducible quadratics. If so we must have one first-degree zero:

Evaluate e^x at x = .01, .1 and .2.
Evaluate 1 + x at x = .01, .1 and .2.
Evaluate 1 + x + x^2 / 2 at x = .01, .1 and .2.
e^.01 = 1.01005
1+.01 = 1.01. Note that this 'misses' e^.01 by .00005.
1+.01+.01^2 = 1.01010. This 'misses' e^.01 by .00005.
e^.1 = 1.10517
1+.1 = 1.1 'misses' e^.1 by about .005
1+.1+.1^2/2 = 1.105 'misses' e^.1 by about .00017
e^.2 =1.22140
1 + .2 = 1.2 'misses' e^.2 by about .021
1 + .2 + .2^2/ 2 = 1.22 'misses' e^.2 by about .001
import 0408, 0410
0415 is test 2 practice
0417 completes practice test and introduces division of graphs
then on to composites etc
finally sex and drugs