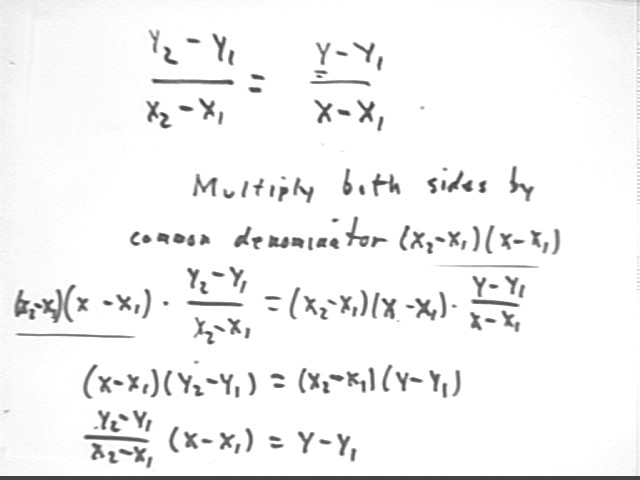
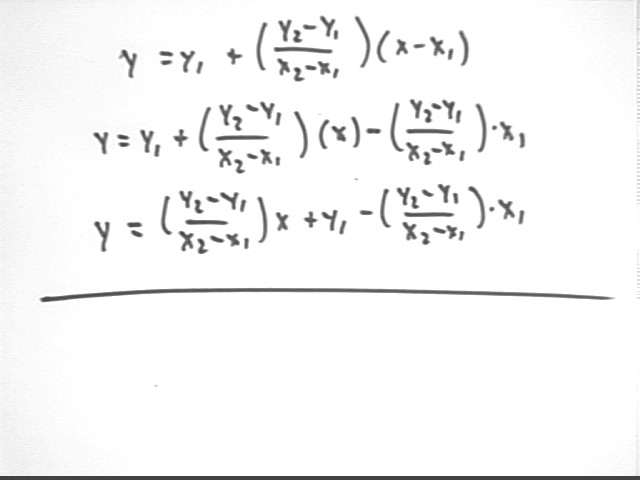
Precalculus I Class 02/06

NOTES ARE MOSTLY PRESENT BUT NOT YET COMPLETED

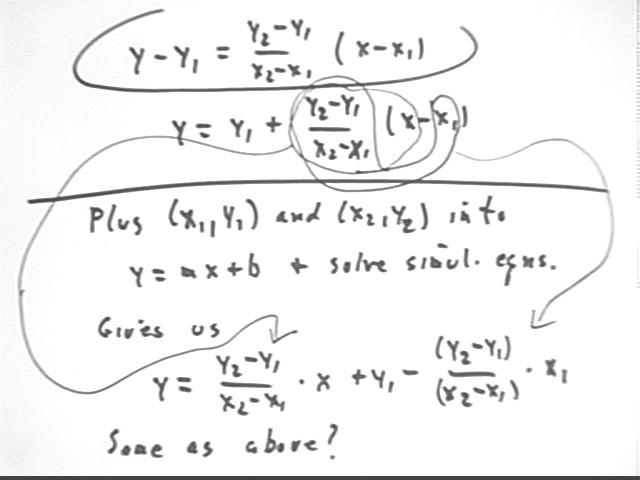
Last class, using two different methods, we obtained the equations

• (y2 - y1) / (x2 - x1) = (y - y1) / (x - x1) and
• y = (y2 - y1) / (x2 - x1) x + y1  - (y2 - y1) / (x2 - x1) x1

to represent a straight line through the two points (x1, y1) and (x2, y2).

Solve both of these equations for y and show that they give you the same result.

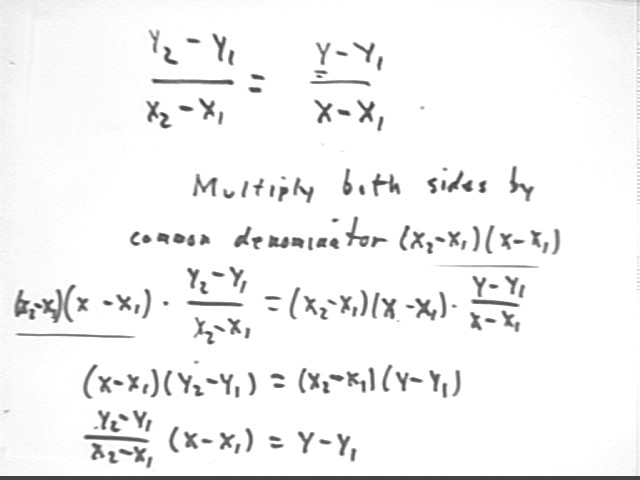
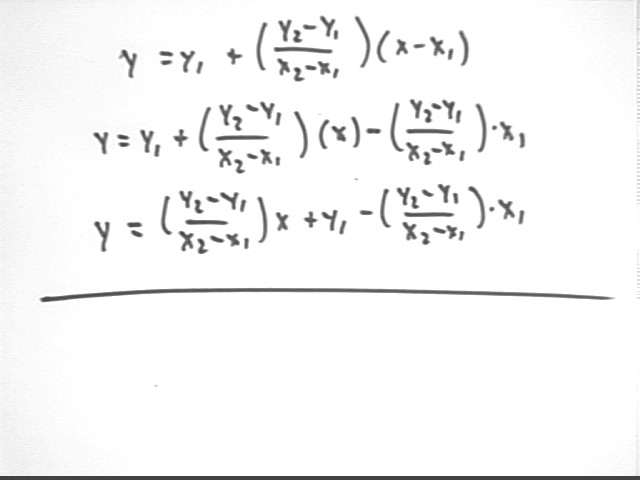
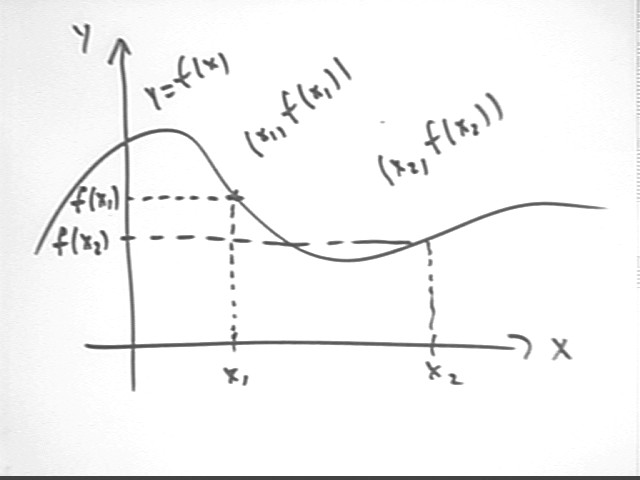
On the graph of y = f(x) vs. x:

• What are the coordinates of the points corresponding to x = x1 and x = x2?

When x = x1 we have y = f(x1) so the coordinates (x, y) of the point are ( x1, f(x1) ).

When x = x2 we have y = f(x2) so the coordinates (x, y) of the point are ( x2, f(x2) ).

• What is the average slope between these points?

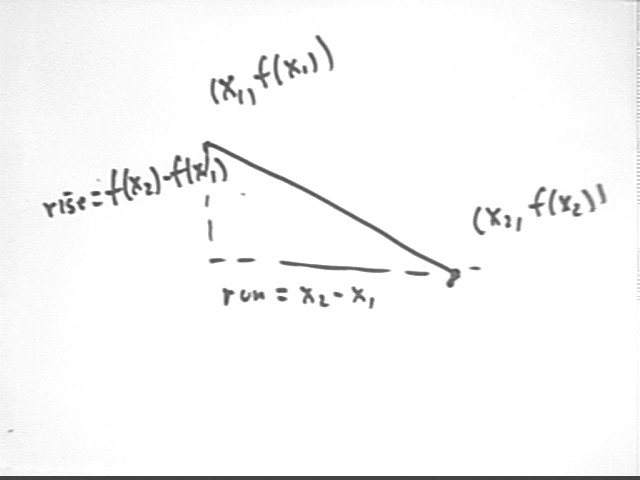
From point 1 to point 2 the rise if f(x2) - f(x1) and the run is x2 - x1.

On a graph of y = depth(t) vs. t:

• What are the coordinates of the points corresponding to t = t1 and t = t2?

When t = t1 we have y = depth(t1) and when t = t2 we have y = depth(t2).  So the coordinates are

• (t1, depth(t1)) and (t2, depth(t2))

• How would you express the average rate at which depth is changing with respect to time, between t = t1 and t = t2?

Ave rate of change of depth with respect to clock time is 

• ave rate = change in depth / change in clock time.

change in depth = depth at t2 - depth at t1 = depth(t2) - depth(t1).

change in clock time = t2 - t1

So we have

• ave rate = ( depth(t2) - depth(t1) ) / (t2 - t1)

If f(t) = .2 t^2 - 6 t + 42:

• Find [ f(t2) - f(t1) ] / (t2 - t1).

f(t2) = .2 t2^2 - 6 t2 + 42

f(t1) = .2 t1^2 - 6 t1 + 42

So 

• f(t2) - f(t1) =  .2 t2^2 - 6 t2 + 42 - (.2 t1^2 - 6 t1 + 42) = .2 ( t2^2 - t1^2) - 6 ( t2 - t1) 

and therefore

• (f(t2) - f(t1) ) / ( t2 - t1) = (.2 ( t2^2 - t1^2) - 6 ( t2 - t1) ) / (t2 - t1).

This expression can be simplified:

t2^2 - t1^2 = (t2-t1) (t2+t1) so we get

( .2(t2-t1)(t2+t1) - 6 ( t2-t1) ) / (t2 - t1) =

.2(t2+t1) - 6.

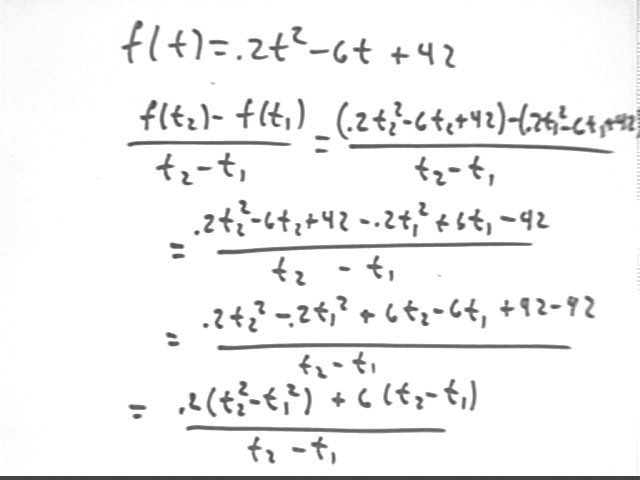
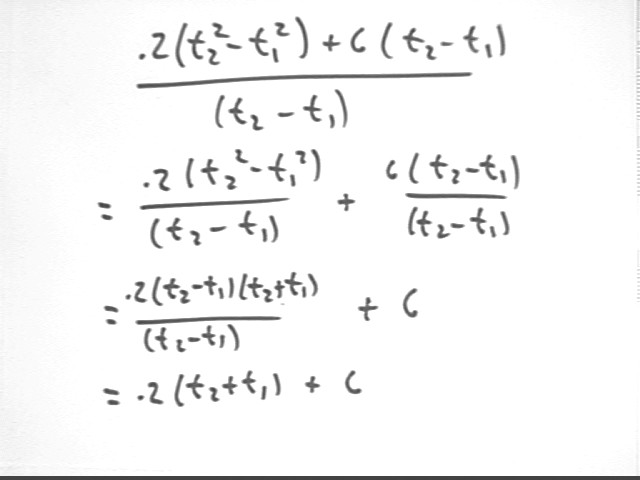
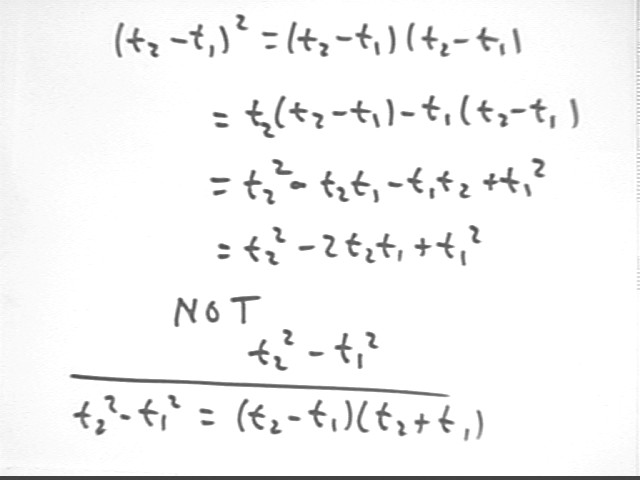
Explain the meaning of f(t2) - f(t1)

f(t2) - f(t1) is the change in the value of the function f between clock times t1 and t2.

• Explain the meaning of t2 - t1.

t2 - t1 represents the change in clock time t 

• Explain the meaning of [ f(t2) - f(t2) ] / (t2 - t1).

[ f(t2) - f(t1) ] / (t2 - t1) represents change in value of f / change in clock time = ave rate of change of f with respect to t.