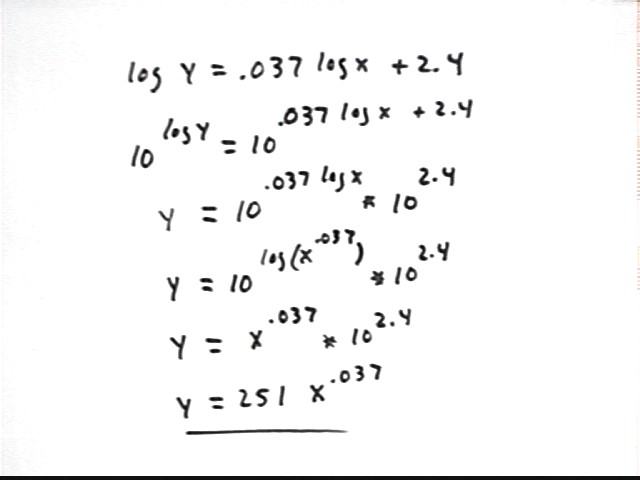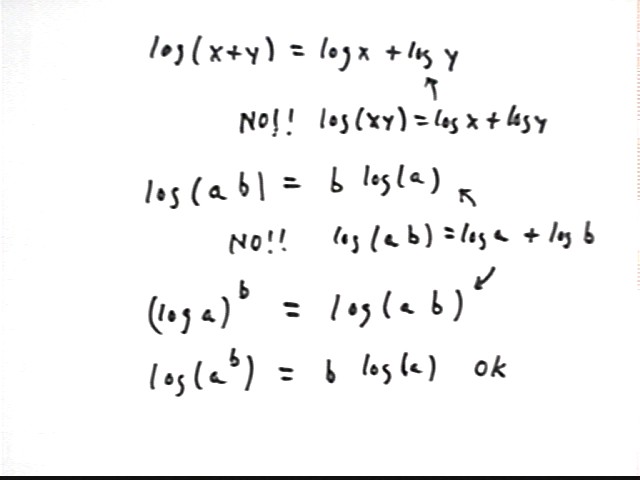
Precalculus I Class 03/27
We note that a formula can 'look right' but be very wrong. Be sure to always check out your operations on logarithms with the laws.
log(x+y) looks like log oughtta distribute over x + y, but there is no reason at all so suppose it does. We might call this the 'fallacy of linearity'. log(x+y) emphatically does not equal log(x) + log(y). Among other things log(x) + log(y) = log(xy), not log(x+y).
log(ab) does not equal b log(a). Among other things b log(a) = log(a^b).
(log a)^b is not log(ab). log(ab) = log(a) + log(b), not (log a)^b.
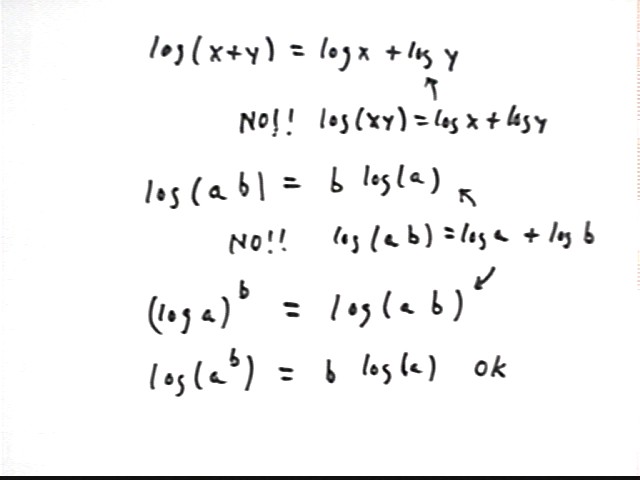
To see why log(ab) = log(a) + log(b), first note that 10(x+y) = 10^x * 10^y, from which it follows that log(10^(x+y) ) = log(10^x * 10^y) = log(10^x) + log(10^y) = x + y.
Whatever a and b are, each can be expressed as a power of 10. If a = 10^x and b = 10^y, which is the case for some x and some y, then log(ab) = x + y. But since a = 10^x, log a = x and since b = 10^y, log b = y, so x + y = log a + log b. It follows that log(ab) = log(a) + log(b).
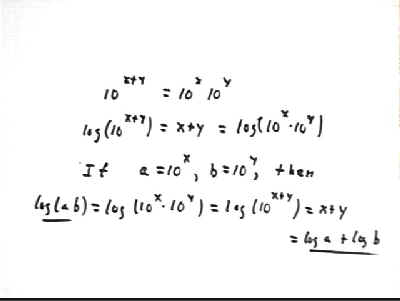
Note that log{base b}(x) is the power of b required to get x.
e.g., log{base 2}(8) is the power of 2 necessary to get 8. Since 2^3 = 8, log{base 2}(8) = 3.
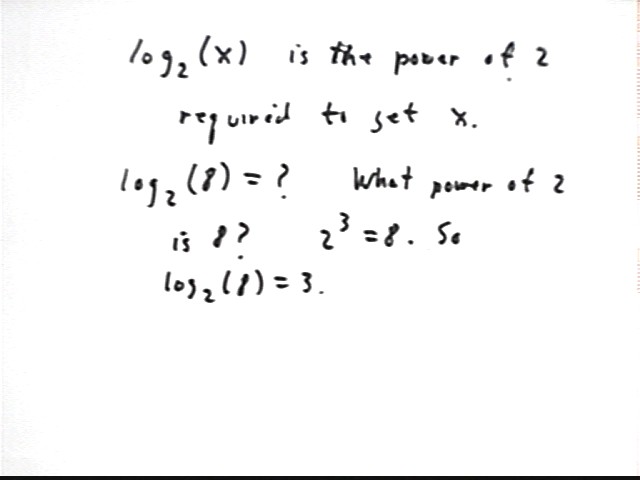
Find these logs:
log{base 2}(16) is the power of 2 we need to get 16.
Trial and error tells us that 2^4 = 16 so log{base 2}(16) = 4.
log{base 3}(81) is the power of 3 we need to get 81.
Trial and error tells us that 3^4 = 81 so log{base 3}(81) = 4.
log{base 5}(125) is the power of 5 we need to get 125.
Trial and error tells us that 5^3 = 125 so log{base 5}(125) = 3.
log{base 4}(64) is the power of 4 we need to get 64.
Trial and error tells us that 4^3 = 64 so log{base 4}(64) = 3.
log{base 4}(32). 4^2 = 16 and 4^3 = 64. So log{base 4}(32) is between 2 and 3.
Observe that 4^2 * 2 = 32, and that 2 = 4^(1/2). So
32 = 4^2 * 4^(1/2) = 4^(2.5) or 4(^5/2). So
log{base 4}(32) = 2.5 or 5/2.
log{base 8}(32). We need the power of 8 that is equal to 32.
We note that 8^(1/3) = 2, and 2^5 = 32. So
8^(1/3)^5 = 8^(5/3). Thus
log{base 8}(32) = 5/3.
Suggested problems:
log{base 25}(125)
log{base 9}(243)
log{base 16}(32)
log{base 27}(243)
log{base 2}(16) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 2}(16) = log(16) / log(2) = 4.
log{base 3}(81) is 4. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 3}(81) = log(81) / log(3) = 4.
log{base 5}(125) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 5}(125) = log(125) / log(5) = 3.
log{base 4}(64) is 3. Verify using your calculator and the identity log{base b}(x) = log x / log b:
log{base 4}(64) = log(64) / log(4) = 3.
log{base 4}(32) is 2.5.
log{base 4}(32) = log(32) / log(4) = 2.5.
log{base 8}(32).
log{base 8}(32) = log(32) / log(8) = 1.66666... .
We solve the equation 5^(7x-3) = 14.
Since our variable x is in the numerator we take the log of both sides to get x out of that numerator, allowing us to use standard algebra to find x.
In the fourth step we have divided both sides by log 5.
In the fifth step we add 3 to both sides.
In the sixth step we multiply both sides by 1/7 and evaluate the resulting expression to find x.
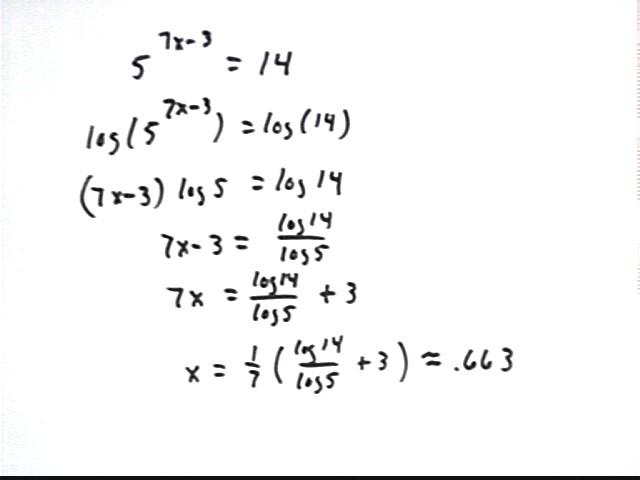
The equation 2^(3x - 4) + 2^(5x - 1) = 7 looks like it should be amenable to the same treatment as in the preceding problem. Taking logs of both sides looks like it should bring the x terms out of the numerator. However there is a serious pitfall in the way of this strategy.
The problem is that log(a+b) is not equal to log a + log b, as we saw earlier. So if after writing
log [2^(3x - 4) + 2^(5x - 1)] = log(7)
we try to say that log(2^(3x-4)) + log(2^(5x - 1) ) = log(7), we are falling into the fallacy of linearity described earlier.
It turns out that this problem cannot be solved to find an exact value of x. We can always approximate the solution, but there is no way to find an exact solution.
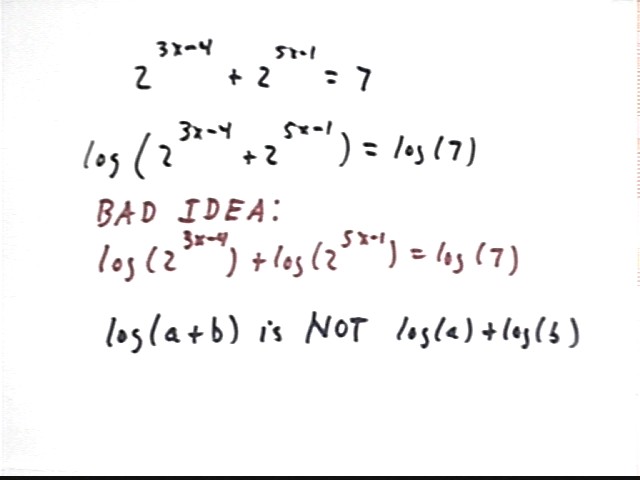
The equation 2^(1/x) = 7 * 2^(x+2) can be solved by taking the log of both sides.
Applying the laws of logarithms we note that log(2^(1/x)) = 1/x * log 2 and log(7 * 2^(x+2) ) = log 7 + log(2^(x+2) and obtain the equation in the third step.
log(2^(x+2) ) = (x + 2) log 2, giving us the equation in the fourth step.
This equation has one denominator, x. Multiplying both sides by this denominator and simplifying gives us that last two steps in the figure below.
The problem is continues on the next figure.
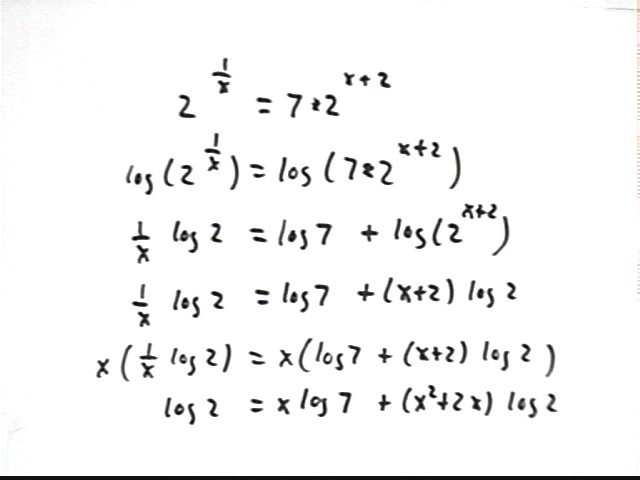
Be sure to understand that log 2 and log 7 are just numbers, which we can easily evaluate using calculators.
We can now see that our equation is quadratic in x, containing x^2, x and constant terms. We will put this equation into the form a x^2 + b x + b and then we will apply the quadratic formula so find values of x which satisfy the equation.
The third line below shows the result of swapping sides and using the distributive law on the expression (x^2 + 2x) log 2.
The fourth line puts x^2, x and constant terms in order, with the log 2 from the right side now appearing as the constant - log 2 on the left. We have also factored x out of the two terms containing just the first power of x.
The fourth line is of form a x^2 + b x + c, with a, b and c as specified below.
We choose to approximate a, b and c before plugging into the quadratic.

Suppose that in linearizing a data set we find that log(y) vs. log(x) gives us a straight line with slope .037 and vertical intercept 2.4. What is the function that models our data?
Our straight line has equation log(y) = .037 log(x) + 2.4. Note that it is important to label the axes with the quantities they actually represent; it would be a very bad idea to label the vertical axis y and the horizontal axis x, since the quantities plotted on those axes are in fact log y and log x.
We want to solve this equation for y.
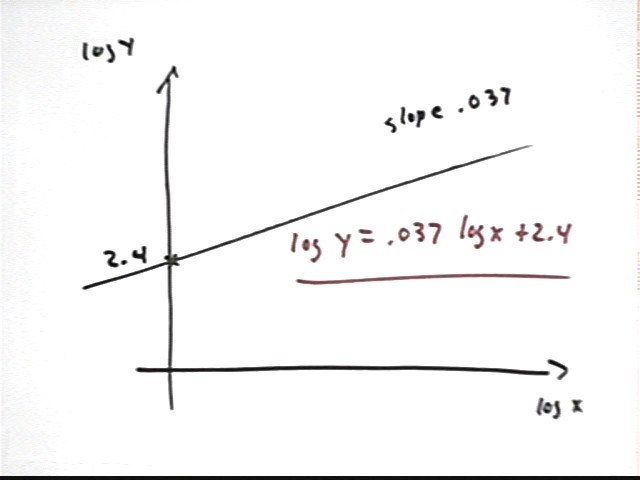
To solve the equation log(y) = .037 log(x) + 2.4 we first write the equation 10^left side = 10^right side, as shown in the second line.
In the third line we simplify using the fact that 10^(log y) = y, and the law of exponents that tells us that 10^(a+b) = 10^a * 10^b.
In the fourth line we rewrite .037 log x as log(x^.037), using the fact that a log(x) = log(x^a).
In the fifth line we use the fact that 10^x and log x are inverse functions to rewrite 10^(log(x^.037)) as just x^.037.
In the last line we evaluate 10^2.4, obtaining 251.
We finally see that the data is modeled by the equation y = 251 x^.037, which is the power function x^p, with p = .037, vertically stretched by factor 251.